Транспортер В-4. Курсовой проект Автоматизированный электропривод цепного транспортера кп140610. 715. Пз разработчик
 Скачать 0.75 Mb.
|
|
Конструктивный расчет датчика ЭДС и звена компенсации В аналоговых системах автоматического управления электроприводами реализация регуляторов и других преобразователей сигналов осуществляется на базе операционных усилителей. П 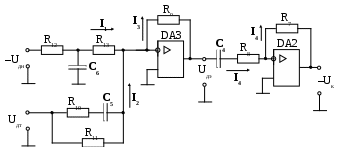 ринципиальная схема датчика ЭДС и звена компенсации показана на рис.11. Фильтр в канале напряжения реализуется на элементах R12, R13, C6. Форсирующее звено в канале тока реализуется на элементах R10, R11, C5. Операционный усилитель DA3 предназначен для суммирования сигналов в датчике ЭДС, что осуществляется путем суммирования токов I1 и I2. Звено компенсации выполнено на операционном усилителе DA2. Элементы входной цепи и цепи обратной связи усилителя DA2 R8, R7, C4 обеспечивают реализацию свойств реального дифференцирующего звена.Рис.11. Принципиальная схема датчика ЭДС и звена компенсации На рис.12 представлена структурная схема для абсолютных величин токов и напряжений, которая соответствует принципиальной схеме, показанной на рис.11. При ее составлении было принято, что сопротивления R12 и R13 одинаковы. 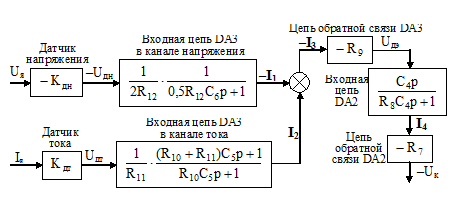 Рис.12. Структурная схема датчика ЭДС и звена компенсации для абсолютных величин От структурной схемы для абсолютных величин перейдем к структурной схеме для относительных величин (рис.13). На данной схеме показаны относительные коэффициенты датчиков напряжения и тока. При переходе от абсолютных величин к относительным величинам в передаточных функциях входных цепей операционных усилителей появляется сопротивление Rбр. В передаточных функциях цепей обратной связи операционных усилителей появляются обратные величины 1/Rбр. 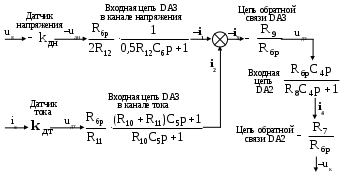 Рис.13. Структурная схема датчика ЭДС и звена компенсации для относительных величин Сопоставляя структурные схемы, показанные на рис.19 и 22, получим соотношения между параметрами математической модели датчика ЭДС и звена компенсации в относительных единицах и параметрами элементов принципиальной схемы. Необходимые коэффициенты передачи обеспечиваются при выполнении условий:       Требуемые значения постоянных времени обеспечиваются при выполнении условий:         Конструктивный расчет регулятора тока На рис.14 показана принципиальная схема регулятора тока и его входных цепей. Регулятор тока выполнен на операционном усилителе DA1. Последовательное включение в цепь обратной связи усилителя DA1 сопротивления R1 и емкости C1 обеспечивает пропорционально-интегральный тип регулятора. На входе усилителя DA1 суммируются три сигнала, приходящие по каналам задания на ток, обратной связи по току и по каналу компенсации ЭДС, путем суммирования токов I1, I2 и I3. В цепи задания на ток и в цепи обратной связи по току установлены фильтры на элементах R2, R3, C2 и R4, R5, C3 соответственно. Нелинейный элемент НЭ1 реализуется на стабилитронах VD1 и VD2. 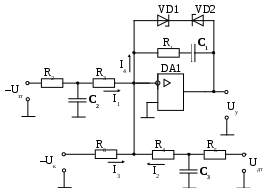 Рис.14. Принципиальная схема регулятора тока и его входных цепей На рис.15 представлена структурная схема для абсолютных величин токов и напряжений, которая соответствует принципиальной схеме, показанной на рис.14. При составлении структурной схемы предполагалось, что сопротивления R2 и R3, а также R4 и R5 одинаковы. От структурной схемы для абсолютных величин перейдем к структурной схеме для относительных величин (рис.16).  Рис.15. Структурная схема регулятора тока и его входных цепей д 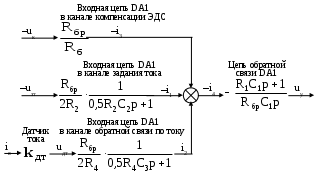 ля абсолютных величинРис.16. Структурная схема регулятора тока и его входных цепей для относительных величин Сопоставляя структурные схемы (см. рис.9 и 16), получим соотношения между параметрами математической модели регулирующей части контура тока в относительных единицах и параметрами принципиальной схемы. Для обеспечения единичных коэффициентов передачи в каналах задания тока, обратной связи по току и компенсации ЭДС должны выполняться условия:  R6=20000 Ом R3=R2=10000 Ом  Требуемые значения постоянных времени обеспечиваются при выполнении условий:    Из записанных соотношений следует выразить и рассчитать параметры элементов принципиальной схемы (сопротивления и емкости). Расчет регулирующей части контура скорости Расчет параметров математической модели контура скорости Рассмотрим структуру и выполним расчет параметров модели контура скорости, используя систему относительных единиц. Структурная схема контура регулирования скорости представлена на рис.17. Контур регулирования тока якоря при его настройке на модульный оптимум рассматриваем как одно звено с передаточной функцией. Контур скорости включает в себя звено регулятора скорости (РС), звено контура тока якоря (КТ), звено умножения на поток и звено механической части привода (МЧ). Обратная связь по скорости при рассмотрении относительных величин принимается единичной. На объект управления действует возмущающее воздействие – момент статического сопротивления, создаваемый нагрузкой на валу двигателя. 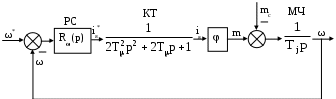 Рис.17. Структурная схема контура регулирования скорости При синтезе регулятора скорости считаем, что момент статического сопротивления равен нулю (режим идеального холостого хода двигателя). При условии mc=0 объект управления в контуре скорости представляется одним звеном:  Передаточная функция регулятора скорости находится по условию настройки контура на модульный оптимум:  Получаем передаточную функцию П-регулятора. Коэффициент передачи регулятора скорости находится по формуле:  Однократная САР скорости является статической по возмущающему воздействию, поэтому в результате появления нагрузки на валу двигателя появляется статическая ошибка по скорости. Определим величину максимальной статической ошибки по скорости:  где mc(max) – максимальный по модулю статический момент на валу двигателя в относительных единицах. Конструктивный расчет регулирующей части контура скорости Принципиальная схема регулирующей части контура скорости представлена на рис.18. Регулятор скорости выполнен на операционном усилителе DA4. Суммирование сигнала задания на скорость и сигнала обратной связи по скорости осуществляется путем суммирования токов I1 и I2. Включение в цепь обратной связи усилителя DA4 сопротивления R16 обеспечивает пропорциональный тип регулятора. Стабилитроны VD3, VD4 реализуют нелинейный элемент НЭ2. 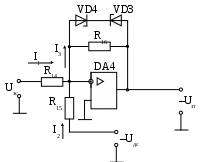 Рис.18. Принципиальная схема регулирующей части контура скорости На рис.19 показана структурная схема для абсолютных величин токов и напряжений, соответствующая принципиальной схеме на рис.18. 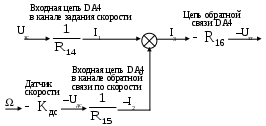 Рис.19. Структурная схема регулирующей части контура скорости для абсолютных величин От структурной схемы для абсолютных величин перейдем к структурной схеме для относительных величин (рис.20). 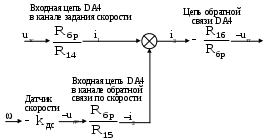 Рис.20. Структурная схема регулирующей части контура скорости для относительных величин Сопоставляя структурные схемы (см. рис.17 и 20), получим соотношения между параметрами математической модели регулирующей части контура скорости в относительных единицах и параметрами элементов принципиальной схемы. Для обеспечения единичных коэффициентов передачи в каналах задания скорости и обратной связи по скорости должны выполняться условия:  R14=Rбр=20000 Ом  Для обеспечения требуемого коэффициента передачи регулятора скорости должно выполняться условие:   Расчет задатчика интенсивности Расчет параметров математической модели задатчика интенсивности Задатчик интенсивности предназначен для формирования линейно изменяющегося во времени сигнала задания на скорость с определенным темпом. Структурная схема задатчика представлена на рис.21. Темп изменения выходного сигнала задатчика определяется уровнем ограничения Q нелинейного элемента (НЭ) и постоянной времени Ти интегратора (И). 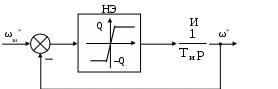 Рис.21. Структурная схема задатчика интенсивности Определим параметры математической модели задатчика интенсивности в относительных единицах. Темп задатчика:  Уровень ограничения нелинейного элемента (принимается): Q=0,9 Постоянная времени интегрирующего звена ЗИ:  Коэффициент передачи в линейной зоне нелинейного элемента (принимается): Кл=100 Конструктивный расчет задатчика интенсивности Принципиальная схема задатчика интенсивности представлена на рис.22. Нелинейный элемент реализуется на операционном усилителе DA7. Ограничение выходного сигнала обеспечивается за счет включения в цепь обратной связи усилителя DA7 стабилитронов VD5 и VD6. Интегратор реализуется на операционном усилителе DA6. Емкость С7 в цепи обратной связи усилителя DA6 определяет постоянную времени интегратора. Усилитель DA5 предназначен для инвертирования сигнала, чтобы обеспечить отрицательную обратную связь, охватывающую нелинейный элемент и интегратор (см. рис.21). 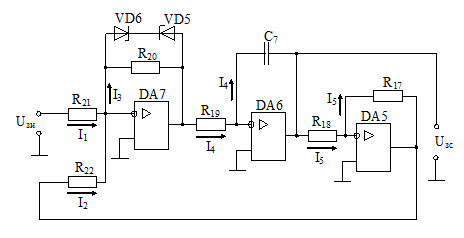 Рис.22. Принципиальная схема задатчика интенсивности Н  а рис.23 показана структурная схема для абсолютных величин токов и напряжений, соответствующая принципиальной схеме на рис.22. Рис.23. Структурная схема задатчика интенсивности для абсолютных величин От структурной схемы задатчика интенсивности для абсолютных величин перейдем к структурной схеме для относительных величин (рис.24).  Рис.24. Структурная схема задатчика интенсивности для относительных величин Из сравнения структурных схем задатчика интенсивности (см. рис.19 и 24) получим соотношения между параметрами математической модели и параметрами элементов принципиальной схемы задатчика. Для обеспечения требуемой постоянной времени интегратора должно выполняться условие RбрС7 = Ти  Для обеспечения требуемого коэффициента передачи в линейной зоне нелинейного элемента должно выполняться условие   Остальные сопротивления в схеме задатчика должны быть таковы, чтобы обеспечить единичные коэффициенты передачи. Для этого должны выполняться следующие условия:  R21=R19=R18=R22=R17=20000 Ом Список используемых источников 1. Евзеров И.Х. и др. Комплектные тиристорные электроприводы: Справ. под ред.В.М.Перельмутера. – М.: Энергоатомиздат, 1988. – 319 с. 2. Томашевский Н.И. и др. Типовые задания к курсовому проекту по основам электропривода. – Свердловск: Изд-во Свердл.инж.пед.ин-та, 1989. - 48 с. 3. Усатенко С.Т., Каченюк Т.К., Терехова М.В. Выполнение электрических схем по ЕСКД: Справ. – 2-е изд., перераб. И доп. – М.: Изд-во стандартов, 1992. – 316 с. 4. Чиликин М.Г., Сандлер А.С. Общий курс электропривода: Учеб. Для вузов. – 6-е изд., доп. И перераб. – М.: Энергоатомиздат, 1981. – 576 с. 5. Шрейнер Р.Т. Системы подчиненного регулирования электроприво-дов. Ч.1: Электроприводы постоянного тока с подчиненным регулированием координат: Учеб.пособие для вузов. – Екатеринбург: Изд-во Урал.гос.проф.-пед.ун-та, 1997. – 279 с. |