Транспортер В-4. Курсовой проект Автоматизированный электропривод цепного транспортера кп140610. 715. Пз разработчик

• Название: Курсовой проект Автоматизированный электропривод цепного транспортера кп140610. 715. Пз разработчик
• Дата: 29.11.2022
• Размер: 0.75 Mb.
• Имя файла: Транспортер В-4.doc
• Тип: Курсовой проект; #818899
• страница: 4 из 5

Выбор сглаживающего реактора

ЭДС преобразователя при угле управления α = 0:

E_d0 = К_еU_2N=1,35^.205=276,75 В

где К_е – коэффициент, зависящий от схемы преобразователя (для трехфазной мостовой схемы К_е=1,35).

Минимальная эквивалентная индуктивность главной цепи по условию ограничения пульсаций выпрямленного тока:



где k_U – коэффициент пульсаций напряжения (для трехфазной мостовой схемы k_U=0,13); p – пульсность преобразователя (для трехфазной мостовой схемы р=6).

Расчетная индуктивность сглаживающего реактора:

L_c = L_э(min) – 2L_т – L_я=0,025-2^.0,00018-0,015=-0,013 Гн

Расчетная индуктивность оказалась отрицательной, следовательно, сглаживающий реактор не требуется. Собственная индуктивность главной цепи достаточно для ограничения пульсаций тока.

4. 
   Расчет параметров математической модели силовой части электропривода
   
   1. 
      Расчет параметров силовой части электропривода в абсолютных единицах
      

Главную цепь системы «тиристорный преобразователь – двигатель» можно представить в виде схемы замещения (рис.4). В главной цепи действуют ЭДС преобразователя E_d и ЭДС якоря двигателя Е_я. На схеме замещения показаны активные сопротивления якорной цепи двигателя R_я, сглаживающего реактора R_c, двух фаз трансформатора 2R_т, а также фиктивное сопротивление R_, обусловленное коммутацией тиристоров. Кроме того, представлены индуктивности якорной цепи двигателя L_я, сглаживающего реактора L_c и двух фаз трансформатора 2L_т. Направления тока и ЭДС соответствуют двигательному режиму электропривода (см. рис.13).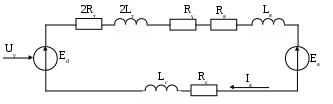



Рис.4. Схема замещения главной цепи

От исходной схемы замещения переходим к эквивалентной схеме (рис.5), где все индуктивности объединяются в одну эквивалентную индуктивность L_э, а все активные сопротивления – в одно эквивалентное сопротивление R_э.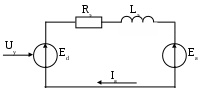




Рис.5. Эквивалентная схема замещения главной цепи
Определим параметры силовой части в абсолютных (т.е. физических) единицах.

Фиктивное сопротивление преобразователя, обусловленное коммутацией тиристоров:



Эквивалентное сопротивление главной цепи:

R_э=R_я +R_с +R_γ+2R_т=0,39+0,055+2^.0,0546=0,55 Ом

Эквивалентная индуктивность главной цепи:

L_э=L_я +L_с+2L_т=0,015+2^.0,00018=0,0158 Гн

Электромагнитная постоянная времени главной цепи:



Электромагнитная постоянная времени цепи якоря двигателя:



Коэффициент передачи преобразователя:



где U_{у max} – напряжение на входе системы импульсно-фазового управления тиристорного преобразователя (напряжение управления), при котором угол управления равен нулю и ЭДС преобразователя в режиме непрерывного тока максимальна. В проекте примем U_{у max}=10 В.

2. 
   Выбор базисных величин системы относительных единиц
   

При рассмотрении модели силовой части электропривода как объекта управления параметры и переменные электропривода удобно перевести в систему относительных единиц. Переход к относительным единицам осуществляется по формуле:

,

где Y – значение в абсолютных (физических) единицах; Y_б – базисное значение (также в абсолютных единицах); y – значение в относительных единицах.

Принимаем следующие основные базисные величины силовой части электропривода:

• 
  базисное напряжение:
  

U_б = E_яN=200,29В

• 
  базисный ток:
  

I_б = I_яN=51А

• 
  базисную скорость:
  

Ω_б = Ω_N=83,73 рад/с

• 
  базисный момент:
  

М_б = M_N=121,99 Н

• 
  базисный магнитный поток:
  

Ф_б = Ф_N=2,39

Базисный ток и базисное напряжение регулирующей части электропривода выбираются так, чтобы они были соизмеримы с реальными уровнями токов и напряжений в регулирующей части. Принимаем:

• 
  базисное напряжение системы регулирования:
  

U_бр= 10 В;

• 
  базисный ток системы регулирования:
  

I_бр=0,5 мА.

Рассчитаем производные базисные величины:

• 
  базисное сопротивление для силовых цепей:
  

• 
  базисное сопротивление для системы регулирования:
  

Механическая постоянная времени электропривода зависит от суммарного момента инерции и принятых базисных значений скорости и момента:

3. 
   Расчет параметров силовой части электропривода в относительных единицах
   

На рис.6 показана структурная схема модели силовой части электропривода как объекта управления. Переменные модели выражены в относительных единицах. В модель входят следующие звенья:

• 
  тиристорный преобразователь (ТП) – пропорциональное звено с коэффициентом передачи k_п;
  
• 
  главная цепь (ГЦ) – апериодическое звено с электромагнитной постоянной времени Т_э и коэффициентом передачи, равным , т.е. эквивалентной проводимости главной цепи в относительных единицах;
  
• 
  механическая часть (МЧ) – интегрирующее звено с механической постоянной времени T_j;
  
• 
  звенья умножения на магнитный поток φ (поток рассматривается в модели как постоянный параметр).
  

Входные величины модели представляют собой управляющее воздействие u_у (сигнал управления на входе преобразователя) и возмущающее воздействие m_c (момент статического сопротивления на валу двигателя).

Переменными модели являются:

• 
  ЭДС преобразователя e_d;
  
• 
  ЭДС якоря двигателя e_я;
  
• 
  ток якоря двигателя i_я;
  
• 
  электромагнитный момент двигателя m;
  
• 
  угловая скорость двигателя ω.
  

Рис.6 Структурная схема объекта управления

Определим параметры электропривода в относительных единицах:

• 
  коэффициент передачи преобразователя:
  

• 
  эквивалентное сопротивление главной цепи:
  

• 
  сопротивление цепи якоря двигателя:
  

• 
  магнитный поток двигателя:
  

.

4. 
   Расчет коэффициентов передачи датчиков
   

Рассчитаем коэффициенты передачи датчиков в абсолютных единицах так, чтобы при максимальном значении величины, измеряемой датчиком, напряжение на выходе датчика было равно базисному напряжению регулирующей части.

Коэффициент передачи датчика тока:



где I_я(max) – максимальный ток якоря по перегрузочной способности двигателя. Максимальный ток определяется по формуле:



Коэффициент передачи датчика напряжения:



Коэффициент передачи датчика скорости:



Рассчитаем коэффициенты датчиков в относительных единицах.

Коэффициент передачи датчика тока:



Коэффициент передачи датчика напряжения:



Коэффициент передачи датчика скорости:

5. 
   Разработка системы управления электроприводом
   
   1. 
      Выбор типа системы управления электроприводом
      

Рассмотрим функциональную схему системы управления электроприводом (рис.7). Система управления электроприводом представляет собой двухконтурную систему автоматического регулирования (САР) скорости. Внутренним контуром системы является контур регулирования тока якоря, внешним и главным контуром – контур регулирования скорости.

Для проектируемого электропривода выбираем однократную систему регулирования скорости. Однократная САР скорости по сравнению с двукратной не обладает астатизмом по возмущающему воздействию (моменту сопротивления), однако для проектируемой системы обеспечение такого астатизма не требуется. Однократная САР скорости обладает лучшими динамическими свойствами по сравнению с двукратной САР. Для контуров регулирования тока якоря и скорости применяется настройка на модульный оптимум. Данную настройку обеспечивают пропорционально-интегральный регулятор тока (РТ) и пропорциональный регулятор скорости (РС). Плавное ускорение и замедление привода обеспечиваются с помощью задатчика интенсивности (ЗИ). Для разгона или торможения привода задатчик интенсивности формирует линейно изменяющийся во времени сигнал задания на скорость.

Сигналы обратных связей поступают в систему регулирования от датчиков тока якоря (ДТ), напряжения якоря (ДН) и скорости (ДС). Датчики состоят из измерительного элемента и устройства согласования. Измерительным элементом для датчика тока якоря является шунт в цепи якоря R_ш, для датчика напряжения – делитель напряжения R_д, для датчика скорости – тахогенератор (ТГ). Устройство согласования обеспечивает необходимый коэффициент передачи датчика и гальваническую развязку силовых цепей от цепей управления. Косвенный датчик ЭДС (ДЭ) вычисляет ЭДС якоря по сигналам датчиков тока и напряжения. Сигнал ЭДС через звено компенсации (ЗК) подается на вход регулятора тока, что требуется для компенсации отрицательного влияния ЭДС якоря на процессы в контуре тока.



Рис.7. функциональная схема системы управления электроприводом
Некомпенсируемая постоянная времени T_μ закладывается в фильтрах Ф1 и Ф2. Эти фильтры обеспечивают защиту объекта управления от высокочастотных помех. Величина T_μ, принятая при проектировании системы, определяет быстродействие контура регулирования тока и всей системы в целом.

Управляющим воздействием на объект управления (силовую часть электропривода) является напряжение управления U_у. Напряжение управления подается на вход системы импульсно-фазового управления тиристорного преобразователя, которая регулирует угол управления, т.е. фазу подачи управляющих импульсов на тиристоры.

Нелинейные элементы НЭ1 и НЭ2 предназначены для ограничения координат системы. Элемент НЭ1 ограничивает выходной сигнал регулятора тока, а следовательно, напряжение управления преобразователя и его выходную ЭДС. Элемент НЭ2 ограничивает выходной сигнал регулятора скорости, тем самым ограничивается сигнал задания тока и сам ток якоря.

2. 
   Расчет регулирующей части контура тока якоря
   
   1. 
      Расчет параметров математической модели контура тока
      

Рассмотрим структуру и выполним расчет параметров модели контура тока, используя систему относительных единиц. Структурная схема контура тока представлена на рис.8. В контуре тока находятся звенья регулятора тока (РТ), фильтра (Ф), тиристорного преобразователя (ТП) и главной цепи (ГЦ). На структурной схеме фильтр показан внутри контура, что эквивалентно наличию фильтра в цепи задания и обратной связи (см. рис.7). Обратная связь по току при рассмотрении относительных величин принимается единичной. На процессы в контуре тока влияет ЭДС якоря двигателя, которую можно считать возмущающим воздействием. При отсутствии ЭДС якоря (якорь неподвижен) в контуре тока можно рассматривать одно звено объекта управления с передаточной функцией: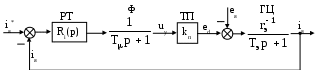



Рис.8. Структурная схема контура регулирования тока якоря

Некомпенсируемую постоянную времени T_μ рекомендуется принять в пределах 0,004–0,01 с.

При синтезе регулятора тока влияние ЭДС якоря не учитывается. Передаточная функция регулятора тока находится по условию настройки контура на модульный оптимум:

.

Получаем передаточную функцию ПИ-регулятора. Параметры регулятора тока находятся по следующим формулам:

Т_i1=T_э=0,029



Контур регулирования тока при настройке на модульный оптимум описывается передаточной функцией фильтра Баттерворта 2-го порядка:



В 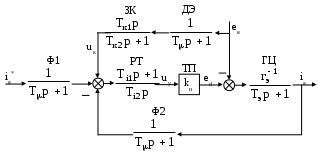лияние ЭДС якоря приводит к появлению статической ошибки по току, что ухудшает качество системы. Для компенсации данного влияния вводится положительная обратная связь по ЭДС якоря. Структурная схема контура тока с компенсацией ЭДС представлена на рис.9. При выносе фильтра из контура он должен оказаться в цепи задания на ток (Ф1), в цепи обратной связи по току (Ф2) и в цепи обратной связи по ЭДС, где его удобно объединить с датчиком ЭДС. Таким образом, датчик ЭДС имеет небольшую инерционность, что является необходимым, т.к. безынерционный датчик ЭДС реализовать невозможно.

Рис.9. Структурная схема контура тока с компенсацией ЭДС

Компенсирующий сигнал u_к подается на вход регулятора тока, а не непосредственно в точку действия ЭДС якоря (между звеньями ТП и ГЦ). Поэтому влияние звеньев регулятора тока и преобразователя на прохождение компенсирующего сигнала необходимо устранить. Это достигается за счет включения в цепь обратной связи по ЭДС звена компенсации. Передаточная функция звена компенсации определяется по формуле:



Таким образом, звено компенсации является реальным дифференцирующим звеном. Параметры звена компенсации находятся по следующим формулам:



Т_к2= T_э=0,029

В результате компенсации ЭДС статическая ошибка по току устраняется.

ЭДС якоря двигателя недоступна для прямого измерения. Косвенный датчик ЭДС якоря использует сигналы тока и напряжения якоря. Связь между током, напряжением и ЭДС якоря следует из уравнения электрического равновесия для якорной цепи. В области изображений по Лапласу это уравнение имеет вид:

e_я(p) = u_я(р) – r_я (T_яр+1)i_я(p)

Реализовать датчик ЭДС в полном соответствии с уравнением невозможно, т.к. требуется идеальное форсирующее звено. Поэтому внесем в датчик инерционное звено с постоянной времени T_μ. В результате уравнение датчика ЭДС принимает вид:



В статическом режиме формулы дают одинаковый результат. Уравнению соответствует структурная схема датчика ЭДС, показанная на рис.19. Также на рис.10 показано звено компенсации.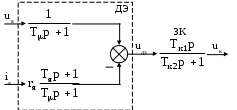


Рис.10. Структурная схема датчика ЭДС и звена компенсации