Курсач Дмиок. курсач Максим нормальные рамки. Курсовой проект способствует закреплению, углублению и обобщению знаний и применению этих знаний к комплексному решению конкретной инженерной задачи по проектированию деталей машин
 Скачать 1.45 Mb.
|
3.2 Определение допускаемых напряжений изгибаДопускаемые напряжения изгиба определим по формуле [1 ч.1, с. 32]  ,где σFO – предел выносливости зубьев по напряжениям изгиба; SF – коэффициент безопасности (принимаем SF=1,75); KFC – коэффициент, учитывающий влияние двухстороннего приложения нагрузки (принимаем KFC=1, т.к. нагрузка – односторонняя); KFL – Коэффициент долговечности (принимаем KFL=1). Т.к. НВ<350, то предел выносливости зубьев: Для шестерен:  .Для колес:  .Определяем допускаемые напряжения изгиба. Для шестерен цилиндрической и конической ступеней:  .Для колес цилиндрической и конической ступеней:  .3.3 Определение допускаемых напряжений при кратковременной перегрузкеОпределяем допускаемые напряжения при перегрузке [1 ч.1, с. 31]. Т.к. твердость материала и цилиндрической, и конической ступени HB<350, то используем формулы  , .Для шестерен цилиндрической и конической ступени:  ; .Для колес цилиндрической и конической ступени:  ; .4 Расчет ступеней редуктора4.1 Расчет тихоходной цилиндрической ступениЦилиндрическую (II) ступень рассчитываем первой, т.к. она является более нагруженной и определяет габариты редуктора. Определяем межосевое расстояние [2, с. 135] 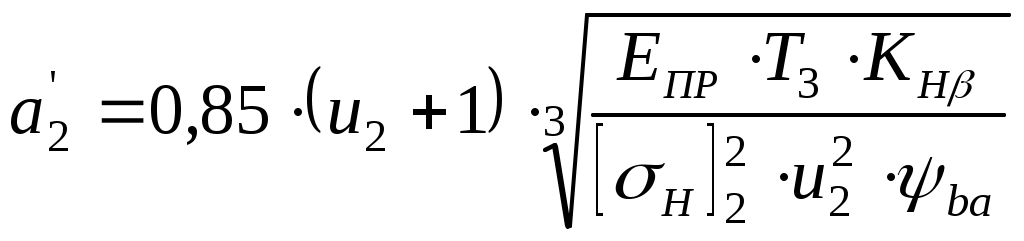 ,где u2 – передаточное отношение II ступени; Епр – приведенный модуль упругости (Епр=210 кПа); Т3 – крутящий момент на выходном валу редуктора;  – коэффициент концентрации нагрузки;[σн]2 – допускаемые контактные напряжения на колесе; ψba – коэффициент ширины колеса относительно межосевого расстояния,  [2, с. 136].Приняв  , находим  [2, с. 135] .По графику [2, с. 130] выбираем 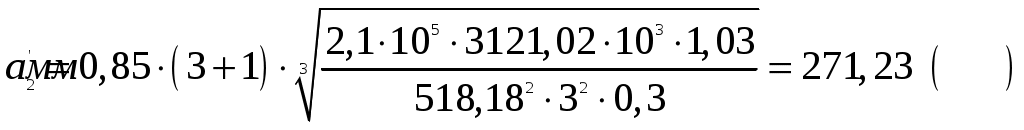 . .Округлив по ряду Ra 40, получим  .Находим ширину колеса  .Приняв  [2, с. 137], находим модуль [2, с. 138] .Принимаем m=3 мм [2, с. 116]. Находим суммарное число зубьев [2, с.179]  .Т.к.  – не целое число, то выбираем m=2,5 мм. Тогда .Число зубьев шестерни [2, с. 180]  .Принимаем  .Число зубьев колеса [2, с. 180]  .Фактическое передаточное отношение  ; .Делительные диаметры шестерни и колеса  ; .Проверочный расчет на усталость по контактным напряжениям Расчет выполняем по формуле  ,где Епр – приведенный модуль упругости (Епр=210 кПа); Т2 – крутящий момент на промежуточном валу;  – коэффициент расчетной нагрузки по контактным напряжениям;d1 – делительный диаметр шестерни;  – ширина колеса; – угол зацепления ( );u2 – передаточное отношение второй ступени. Коэффициент расчетной нагрузки по контактным напряжениям определим по формуле [2, с. 127]  ,где – коэффициент концентрации нагрузки; – коэффициент динамической нагрузки.Для определения коэффициента динамической нагрузки сначала найдем окружную скорость  .Назначаем 9-ю степень точности [2, с. 119]. Принимаем  [2, с. 132]. Тогда Определяем контактные напряжения  . – условие прочности выполняется.При этом расхождение составляет  .Поэтому производим перерасчет ширины колеса 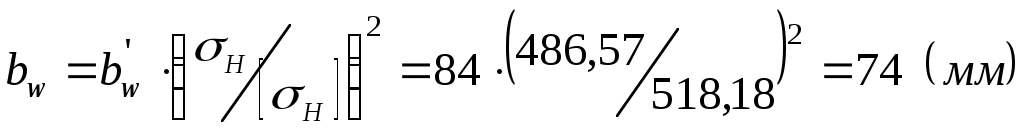 .Проверочный расчет по напряжениям изгиба Напряжения изгиба определяем по формуле [2, с.140]  ,где  – коэффициент формы зуба; – окружная сила; – коэффициент расчетной нагрузки по напряжениям изгиба; – ширина колеса;m – модуль. При х=0 находим коэффициенты формы зуба [2, с. 140] Для шестерни:  ;Для колеса:  .Дальнейший расчет выполняем по тому из колес, у которого меньше  Для шестерни:  ;Для колеса:  .Расчет ведем по колесу. Определяем окружную силу  .Коэффициент расчетной нагрузки по напряжениям изгиба определяется аналогично коэффициенту расчетной нагрузки по контактным напряжениям  ,где  – коэффициент концентрации нагрузки; – коэффициент динамической нагрузки. [2, с. 130];  [2, с. 132]. Определяем напряжения изгиба  . – условие прочности выполняется.Проверочный расчет на заданную перегрузку Определяем максимальные контактные напряжения и напряжения изгиба [2, с. 174]  . . . .Условия прочности выполняются. Определим также диаметры выступов и впадин Для шестерни:  ; .Для колеса:  ; . |