Курсач Дмиок. курсач Максим нормальные рамки. Курсовой проект способствует закреплению, углублению и обобщению знаний и применению этих знаний к комплексному решению конкретной инженерной задачи по проектированию деталей машин

• Название: Курсовой проект способствует закреплению, углублению и обобщению знаний и применению этих знаний к комплексному решению конкретной инженерной задачи по проектированию деталей машин
• Анкор: Курсач Дмиок
• Дата: 06.09.2022
• Размер: 1.45 Mb.
• Имя файла: курсач Максим нормальные рамки.doc
• Тип: Курсовой проект; #664998
• страница: 4 из 13

4.2 Расчет быстроходной червячной ступени

Принимаем число заходов червяка .

Тогда

,

что удовлетворяет условию .
Принимаем коэффициент диаметра червяка ( ). При этом

– лежит в рекомендуемых пределах.
Определяем приведенный модуль упругости

,
где – модуль упругости стали;

– модуль упругости бронзы.
Находим межосевое расстояние [2, с. 208]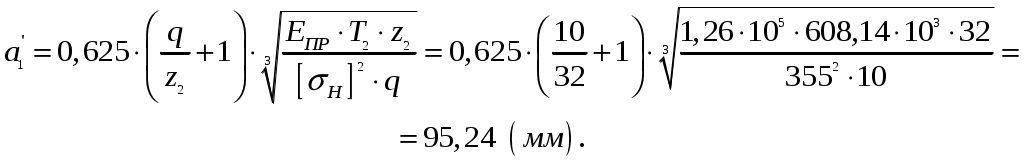

Округляя по ряду Ra 40, получим: .
Определяем модуль [2, с. 201]

.
Принимаем m=5 мм [2, с. 201].
Определяем коэффициент смещения [2, с. 202]

.
Это значение необходимо уменьшить.

Примем и . Тогда

.
Находим делительные диаметры червяка и червячного колеса

;

.
Проверяем выбранное значение скорости скольжения V_S.

Определим угол подъема винтовой линии [2, с. 201]

.

.
Определяем окружную скорость
.
Тогда скорость скольжения [2, с.204]
.
Уточняем значение допускаемых контактных напряжений

.
Проверочный расчет по контактным напряжениям

Контактные напряжения определим по формуле [2, с. 208]
,
где – коэффициент расчетной нагрузки по контактным напряжениям;

– угол подъема винтовой линии;

– угол, соответствующий половине дуги обхвата червяка колесом ( );

– торцовый коэффициент перекрытия;

– коэффициент, учитывающий уменьшение длины контактной линии ( ).
Определяем торцовый коэффициент перекрытия [2, с. 208]

.
При частоте вращения



окружная скорость [2, с. 204]

.
Определяем коэффициент расчетной нагрузки [2, с. 210]

, т.к. .

– при постоянной нагрузке

.
Определяем контактные напряжения

.
– условие прочности выполняется.
Проверочный расчет по напряжениям изгиба
Напряжения изгиба определяем по формуле [2, с. 209]
,
где – коэффициент формы зуба;

– окружная сила на червячном колесе;

– коэффициент расчетной нагрузки по напряжениям изгиба;

– ширина колеса;

– нормальный модуль.
Определяем окружную силу

.
Определяем коэффициент расчетной нагрузки [2, с. 210]

.

Определяем нормальный модуль

.
Диаметр вершин выступов [2, с. 201]

.
Ширина червячного колеса [2, с. 202]

.

Принимаем .
Определяем эквивалентное число зубьев колеса [2, с. 209]

.
Принимаем коэффициент формы зуба [2, с. 209]
Определяем допускаемые напряжения изгиба [2, с. 211]
.
Определяем напряжения изгиба
.
– условие прочности выполняется.
Уточняем КПД

Приняв угол трения [2, с. 205], получим

.
Определяем оставшиеся необходимые размеры

Для червяка:

Диаметр впадин

;

Длина нарезаемой части [2, с. 201]

.

Принимаем (увеличили на 25 мм, т.к. m<10).

Для червячного колеса:

Диаметр вершин выступов [2, с. 202]

;

Диаметр впадин [2, с. 202]

;

Диаметр, соответствующий углу обхвата червяка в 100⁰ [2, с. 202]

.

Назначаем 8-ю степень точности [2, с. 203].