Курсач Дмиок. курсач Максим нормальные рамки. Курсовой проект способствует закреплению, углублению и обобщению знаний и применению этих знаний к комплексному решению конкретной инженерной задачи по проектированию деталей машин

• Название: Курсовой проект способствует закреплению, углублению и обобщению знаний и применению этих знаний к комплексному решению конкретной инженерной задачи по проектированию деталей машин
• Анкор: Курсач Дмиок
• Дата: 06.09.2022
• Размер: 1.45 Mb.
• Имя файла: курсач Максим нормальные рамки.doc
• Тип: Курсовой проект; #664998
• страница: 5 из 13

5 Расчет открытой конической ступени

Определяем диаметр внешнего сечения колеса по формуле [2, с. 155]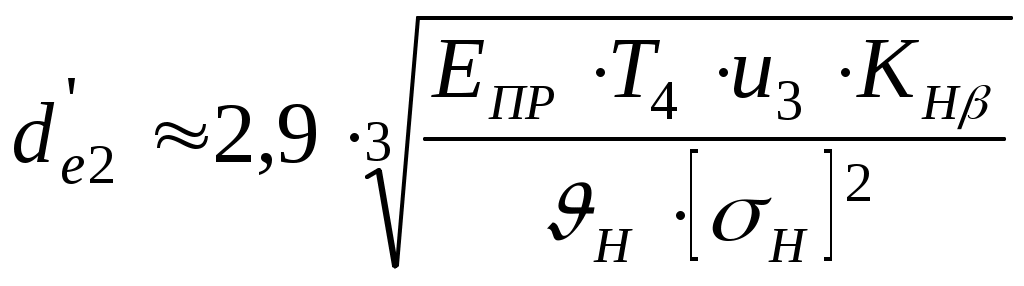
,
где – коэффициент концентрации нагрузки;

– коэффициент, характеризующий понижение прочности конической передачи по сравнению с цилиндрической.
Т.к. , то принимаем [2, с. 156].
Т.к. НВ₁ и , то [2, с. 158]

.
Тогда диаметр внешнего сечения

.
Определяем внешнее конусное расстояние [2, с. 182]

.
Приняв коэффициент ширины зубчатого венца относительно внешнего конусного расстояния , определяем ширину зубчатого венца [2, с. 155]

.
Определяем геометрические параметры
Определяем углы делительных конусов [2, с. 152]

, тогда ;

.

Определяем диаметр внешнего сечения шестерни

.
Далее ведем расчет по параметрам среднего сечения, где [2, с. 182]

.
Выбираем число зубьев шестерни [2, с. 158].
Т.к. НВ₁ и , то число зубьев шестерни определяется по формуле [2, с. 158]

.

Округляем: .
Определяем модуль [2, с.158]
.
Принимаем расчетный угол [2, с. 157].

Тогда

.

Округляем до стандартного: .
При этом

.
Число зубьев шестерни

.
Окончательно принимаем .
Определяем число зубьев колеса

.
Определяем диаметры средних сечений

;

.
Проверочный расчет по контактным напряжениям
Определяем окружную скорость

.
Назначаем 9-ю степень точности [2, с. 119].
Выбираем [2, с. 132].
Тогда коэффициент расчетной нагрузки

.
Условие прочности по контактным напряжениям [2, с. 154]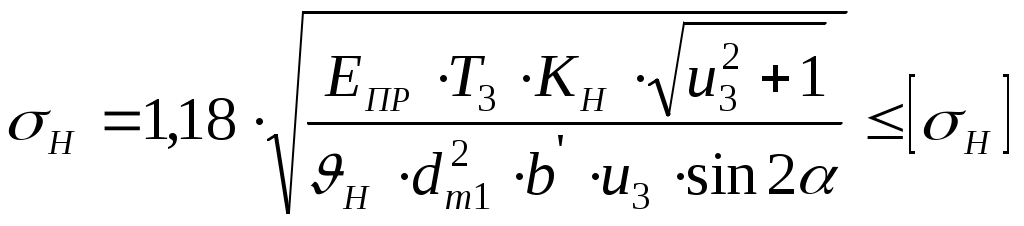


.
– условие прочности выполняется.
.
Окончательно принимаем .
Проверочный расчет по напряжениям изгиба
Напряжения изгиба определяем по формуле [2, с. 153]
,
где – коэффициент формы зуба;

– окружная сила;

– коэффициент расчетной нагрузки по напряжениям изгиба;

– ширина колеса;

– модуль среднего сечения;

– коэффициент, характеризующий понижение прочности конической передачи по сравнению с цилиндрической.
Выбираем коэффициент динамической нагрузки [2, с. 132].
Определяем коэффициент концентрации нагрузки [2, с. 156]

.
Коэффициент расчетной нагрузки по напряжениям изгиба

.
Т.к. НВ₁ и , то [2, с. 158]

.
Определяем окружную силу

.
Определяем коэффициенты смещения [2, с. 158]

;

.
Определяем число зубьев биэквивалентных шестерни и колеса [2, с. 157]

;

.
Находим коэффициенты формы зуба [2, с. 140]

Для шестерни: ;

Для колеса: .
Дальнейший расчет выполняем по тому из колес, у которого меньше

Для шестерни: ;

Для колеса: .
Расчет ведем по колесу
.
.
Т.к. всего на 3,4 % и т.к. основным критерием является прочность по контактным напряжениям, то считаем, что условие прочности выполняется.
Определяем другие геометрические параметры
Среднее и внешнее конусные расстояния [2, с. 152]

;

.
Диаметр внешнего сечения шестерни [2, с. 152]

.
Диаметр внешнего сечения колеса

,

где

[2, с. 152].