Лабораторный практикум_Термодинамика. Лабораторная работа 1 калориметрия раздел " Термодинамика" лабораторная работа " калориметрия" Цель работы
 Скачать 0.6 Mb.
|
Последовательность выполнения работыДля проведения работы берут набор пронумерованных пробирок, содержащих смеси фенола и воды различного составаФ Е Н О Л % В О Д А %10 90 20 80 30 70 40 60 50 50 60 40 70 30 80 20 Пробирки по очереди нагревают на водяной бане, температура которой измеряется простым химическим термометром. Нагревая смесь, встряхиваем время от времени пробирку, пока температура не достигла определенного для каждой смеси значения, смесь остается мутной. Выше этой температуры она становится прозрачной, тогда нагревание бани прекращают и внимательно следят за падением температуры, отмечая ту температуру, при которой смесь снова начинает мутнеть в результате наступления расслаивания. Чтобы получить достаточно точные результаты, надо температуру изменять медленно и непрерывно перемешивать содержимое пробирок (во избежание перегрева и переохлаждения). Для каждой смеси заносят температуру в таблицу и строят кривую, откладывая на оси абсцисс процентный состав смеси, а на оси ординат – температуру расслаивания. Температура расслаивания, отвечающая максимуму кривой, является критической температурой растворения. Отчет о работеРезультаты опытов заносят в таблицу:
После получения всех температурных точек, отвечающих равновесию соответствующих фаз, необходимо построить график, нанеся на оси абсцисс состав (весовой % фенола или воды), а на оси ординат — температуру (tср.). Диаграмма должна быть построена на миллиметровой бумаге в масштабе с делениями не меньше чем 1 см = 10% и 1 см = 5°. Контрольные вопросы Какие возможны типы бинарных жидких растворов с ограниченной взаимной растворимостью? Привести примеры. В чем состоит правило прямой линии Алексеева и его практическое значение? Проверить правило Алексеева на полученной экспериментальной кривой. Что такое конноды? Сколькими степенями свободы обладают системы, если точка заданного состава находится вне кривой и в критической точке? Сформулировать правило фаз Гиббса. Уметь рассчитывать степень свободы в различных точках диаграммы (рисунок 2). Показать на рисунке 2 линии ликвидус и солидус. ЛитератураКиреев В.А. Курс физической химии, Госхимиздат, М-Л. 1955 Киселева Е.В., Каретников Г.С., Кудряшов И.В. Сборник примеров И задач по физической химии, Изд-во «Высшая школа», 1965, с. 135. Горбачев С.В. Практикум по физической химии, Изд-во «Высшая школа», М., 1966, стр. 239-246. Егорова И.В., Новик С.Н. Фазовые равновесия. Методическая разработка. Караганда, 1983г. МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН КАРАГАНДИНСКИЙ УНИВЕРСИТЕТим. Е. А. БУКЕТОВА Химический факультет Кафедра физической и аналитической химииЛАБОРАТОРНАЯ РАБОТА №3 ПОСТРОЕНИЕ ИЗОТЕРМИЧЕСКОГО РАЗРЕЗА В ГЕТЕРОГЕННОЙ ТРЁХКОМПОНЕНТНОЙ СИСТЕМЕ Раздел: Термодинамика ЛАБОРАТОРНАЯ РАБОТА «ПОСТРОЕНИЕ ИЗОТЕРМИЧЕСКОГО РАЗРЕЗА В ГЕТЕРОГЕННОЙ ТРЁХКОМПОНЕНТНОЙ СИСТЕМЕ» Цель работы: Ознакомление с частичной растворимостью жидких веществ в тройной системе и построение изотермы растворимости. Теоретическая часть Если из трёх компонентов два (В и С) ограниченно растворимы друг в друге, а третий компонент (А ) растворяется в н и х неограниченно, то прибавление последнего увеличивает взаимную растворимость первых двух компонентов вплоть до образования гомогенной системы. Три жидкости, слитые вместе, при ограниченной растворимости могут дать три основных типа взаимного распределения друг в друге: 1) вещества А ,В и С даю т три пары частично смешивающихся друг с другом жидкостей, то есть н и одно не растворяется полностью в другом ; 2) из трёх веществ имеем две частично растворимые пары (например, A в В и А в С), но есть пара, полностью растворимая друг в друге (В в С); 3) три вещества (А , В и С) даю т всего одну пару частично смешивающихся д руг в друге жидкостей (например, А в В ), а пары А -С и В -С полностью растворимы в любых отношениях. Наиболее простым для экспериментального исследования является третий случай. Для построения полной диаграммы состояния трёхкомпонентной системы требуется четырехкоординатная система (давление P, температура Т, молярные доли компонентов х А и х в). Чтобы изобразить трёхкомпонентную систему на плоской диаграмме, необходимо принять условия Р=const и T=const. Состав же тройной системы на плоскости удобно выражать треугольной диаграммой Гиббса- Розебома (рис. 1). Вершины равностороннего треугольника соответствую т чисты м веществам А , В и С. Точки на сторонах треугольника отвечают составам двухкомпонентных систем А -В , А -С и В -С . Каждая точка внутри треугольника изображает состав тройной смеси. Существуют два метода определения состава трёхкомпонентной системы. По Гиббсу за 100% принимается высота правильного треугольника. При этом сумма длин перпендикуляров, опущенных из любой точки внутри треугольника на его стороны, есть величина постоянная и равна высоте этого треугольника. Процентное содержание каждого компонента определяется расстоянием от точки , отражающей состав системы (точки P на рис.1а), до стороны треугольника, противолежащей вершине, соответствующей чистому компоненту. 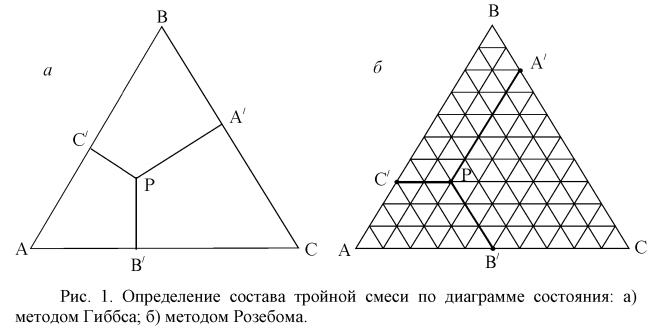 На рис. 1а отрезок РА соответствует процентному содержанию компонента А, РВ - содержанию компонента В, РС - содержанию компонента С . По методу Розебома за 100% принимается длина стороны правильного треугольника. Сумма отрезков, проведённых параллельно сторонам треугольника из точки P (РА + РВ + РС на рис.1б) равна стороне треугольника. Здесь содержание компонента А - длина отрезка РА'; содержание В - длина отрезка РВ'; содержание компонента С - длина отрезка PC'. Оба метода приводят к одинаковым результатам, так ка к стороны и высоты равностороннего треугольника пропорциональны друг другу. В данной работе должна быть построена изотерма растворимости для тройной системы А + В + С, состоящей из двух взаимно нерастворимых компонентов и третьего компонента, неограниченно растворимого в первых двух. Система в этом случае (при определённых концентрациях) расслаивается на две равновесные фазы. Очевидно, в этом случае на диаграмме должны быть отмечены две сопряжённые области: гомогенная и гетерогенная, которые отделены друг от друга главной кривой. Эта кривая и есть совокупность точек, выражающих составы сосуществующих фаз, и представляет собой контур, определяющий границу расслаивания. Диаграмма, на которой нанесён этот контур, называется диаграммой изотермы взаимной растворимости трёх жидкостей. До работы следует ориентировочно представить себе положение области расслаивания в треугольнике Гиббса. Если, например, даны вода (А), этиловый спирт (В) и бензол (С), то известно, что вода и бензол при комнатной температуре очень слабо взаимно растворимы, тогда как этиловый спирт неограниченно растворим и в воде, и в бензоле. Следовательно, области расслаивания должна захватить практически полностью сторону АС треугольника на рисунке 2. Таким образом, область АКСА – область равновесного сосуществования двух жидких фаз L1 и L2. Область АВСКА – гомогенная область сосуществования жидкости L. Экспериментальная часть Работа состоит из двух серий опытов, дающих две смыкающиеся половинки кривой, ограничивающей область расслаивания. Принадлежности для работы: 2 бюретки, 10 колбочек, 2 пипетки, градуированные по 0,1 мл, бланки с треугольной сеткой (каждая из высот равностороннего треугольника пересекается перпендикулярами, делящими высоту на 10 равных частей). Для первой серии опытов готовятся растворы:
Количество мл А + В следует рассчитать так, чтобы в сумме было 5 мл. Полученные смеси оттитровать компонентом С до появления мути, свидетельствующей о перенасыщении раствора компонентом С. Титровать нужно осторожно, колбу непрерывно встряхивать. Для нахождения точки тройного состава, находящейся на кривой расслаивания, необходимо рассчитать % объёмного содержания компонента С в смеси.   Нахождение точки тройного состава ведётся следующим образом: вершину треугольника С соедините линией с точкой противоположной стороны D , отвечающей исходному двойному составу (A+B).Таким образом, эта линия AD будет отвечать изменению концентрации количества С от 0 (т. D) до 100% (С) при фиксированном соотношении А:B=BD:AD. Меняя отношение А:В, получаем набор точек, отвечающих кривой расслаивания. Во второй серии опытов готовят растворы следующих составов: 10% + 90%; 20% + 80%; 30% + 70%; 40% + 60%; 50% + 50%; В+С. Вторая половина кривой строится таким же образом, но растворы титруются компонентом А. следует иметь в виду, что компоненты А и С выбирают таким образом, чтобы они были взаимно нерастворимы, например, вода (А) и бензол (С). Если ветви кривой, построены по результатам первой и второй серий опытов, имеет большой промежуток между точками D и F, следует выбрать самостоятельно несколько составов, чтобы получить дополнительные точки. Только в этом случае кривая расслаивания будет завершённой. 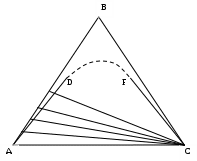  Рисунок 2. Изотерма растворимости трехкомпонентной системы О  тчёт о работеДанные расчёта занести по следующему образцу:
По полученным данным построить изотерму растворимости и обозначить области: гетерогенную и гомогенную. Опыт можно повторить при иной температуре, проследив за изменением взаимной растворимости. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||