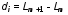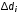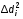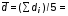Колебания и волны. Лабораторная работа 2к определение параметров физического маятника Введение
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
|
4.3. Включить 3Г и ВУ в сеть. Дать приборам прогреться несколько минут. Поместить на чашечку гирьку массой m = 20 г. Сила натяжения струны рассчитывается как Т = (m + m0)g. (8) Так как проволока имеет малый диаметр и ее легко порвать, нужно обращаться с ней достаточно осторожно. 4.4. Ручку «множитель» генератора 3Г поставить в положение 1, ручку «усиление» - в крайнее правое положение. Установить наименьшую частоту (20 Гц). 4.5. Плавно увеличивая частоту, добиться установления на струне основной моды колебаний с наибольшей амплитудой. Наблюдать колебания удобнее сверху, а не с боку. Записать значение частоты в табл. 3. Там же зарисовать профиль струны. 4.6. Продолжая увеличивать частоту 3Г, добиться установления следующих (n = 2, 3, 4, 5) мод колебаний струны. Соответствующие частоты и профили поместить в табл. 3. Таблица 3
4.7. Записать значения массы гирек (20г) и частоты первой моды также в табл. 4. 4.8. Поместить на чашечку гирьки с общей массой m = 30 г. Добиться установления основной моды (см. 4.5), записать значения m и частоты колебаний i в табл. 4. 4.9. Повторить измерения по пункту 4.8 для масс 40, 50, и 60 г; данные поместить в табл. 4. Таблица 4
5. Обработка результатов измерений 5.1. По данным табл. 3 рассчитать длину волны ln, частоту nn и скорость распространения Vi = 2Li, внести эти значения в табл. 3. Рассчитать среднее значение скорости распространения 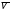 (для разных мод колебаний): (для разных мод колебаний):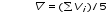 . (9) . (9)5.2. Зная 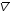 и силу натяжения струны Т, рассчитать погонную плотность струны ρ0: и силу натяжения струны Т, рассчитать погонную плотность струны ρ0: 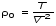 (10) 5.3. По данным табл. 4 рассчитываются экспериментальные значения скорости распространения волны для основной моды при разных значениях силы натяжения струны: (10) 5.3. По данным табл. 4 рассчитываются экспериментальные значения скорости распространения волны для основной моды при разных значениях силы натяжения струны: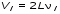 . (11) . (11)5.4. Абсолютную ошибку скорости ∆Vi можно рассчитать так: 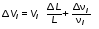 , (12) , (12)где ∆L и ∆i - приборные ошибки в измерении длины струны и частоты колебаний. 5.5. Используя значения ρ0 и предварительно рассчитав по формуле (8) Тi, вычислить теоретические значения скорости распространения (7). Данные расчетов занести в табл. 4. Сравнить полученные данные по экспериментальным и теоретическим значениям скоростей распространения для различных Тi. Литература 1. Савельев, И.В. Курс общей физики. T.4. Волны. Оптика / И.В.Савельев.- М.: Изд-во « Астрель», 2001. Приложение Пусть в положительном направлении оси 0X по струне поперечная волна смещения 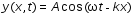 . (13) . (13)Рассмотрим бесконечно малый элемент струны dlоколо горба волны cx = 0 при t = 0 (рис. 3). 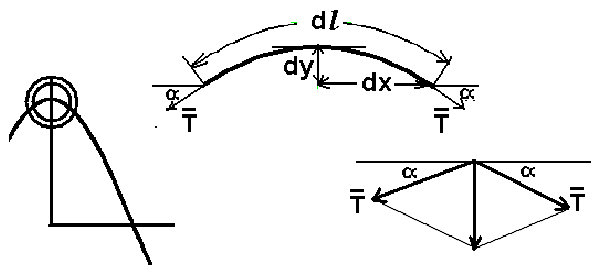 Рис.3 По второму закону Ньютона ускорение этого элемента определяется как 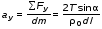 , (14) , (14) где Т - сила натяжения струны; 0 - ее погонная плотность. Смысл остальных величин ясен из рис. 3, пользуясь которым, находим 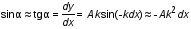 ; (15) ; (15) 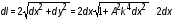 . (16) . (16)Тогда из (14), (15) и (16) 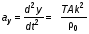 . (17) . (17)Находя 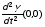 непосредственно из формулы (13) и сравнивая с (17), получим непосредственно из формулы (13) и сравнивая с (17), получим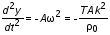 . (18) . (18)Откуда скорость распространения бегущих по струне поперечных волн определится, как указано в 2.5, формула (7) 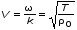 . . Вопросы для самоконтроля 1-й КОМПЛЕКТ 1. Дайте определение волны. Какие волны называются продольными, поперечными? Какие волны изучаются в настоящей работе? 2. Напишите граничные условия для струны, закрепленной на обоих концах. Найдите спектр собственных частот . 3. Как меняется фаза волны при отражении? 2-й КОМПЛЕКТ 1. Напишите уравнение гармонической волны, распространяющейся в упругой среде. Назовите её параметры. 2. Что называется узлами и пучностями в стоячей волне? Как связано расстояние между соседними узлами с длиной волны? 3. В чем заключается явление резонанса, и какую роль оно играет в данной работе? 3-й КОМПЛЕКТ 1. Напишите уравнения скорости и ускорения движения частиц среды при распространении волны. 2. Дайте определение длины волны, фазовой скорости, частоты и периода колебания. Как связаны эти величины? 3. Напишите формулу, связывающую частоту любых нормальных колебаний струны с основной частотой. 4-й КОМПЛЕКТ 1. Дайте определение волновой поверхности и волнового фронта. 2. Напишите выражения для бегущей и стоячей волн. Объясните их различие. 3. Найдите спектр собственных частот колебаний упругой узкой тонкой пластины, если один конец её закреплен, а второй свободен. 5-й КОМПЛЕКТ 1. Напишите дифференциальное волновое уравнение. Каковы его решения? 2. Выведите формулу для вычисления скорости волны при установлении на струне нормальных колебаний основной частоты. 3. Сколько длин волн укладывается на струне при наблюдении первой, второй и третьей гармоник основной частоты? 6-й КОМПЛЕКТ 1. Что является вынуждающей силой, действующей на струну? 2. Найдите спектр собственных частот колебаний струны при данных граничных условиях (4). 3. Напишите уравнение стоячей волны. Приведите её график. Покажите узлы и пучности. Работу поставили, написали описание и составили вопросы для самоконтроля ст. преподаватель Афанасьев Б.Л. и доцент Ипполитова Г.К. Лабораторная работа № 11-К «Определение скорости звука в воздухе» 1. Введение 1.1. Важнейшей характеристикой любой однородной среды, связанной с её упругими и инертными свойствами, является скорость распространения звуковых волн. Звуковыми обычно называют упругие волны, частоты которых лежат в диапазоне от 20 до 20000 Гц. 1.2. Прямые измерения скорости звука в воздухе (например, по времени прохождения звуковым импульсом заданного расстояния) в лабораторных условиях осуществить трудно (и шумно). В данной работе скорость звука определяется методом стоячих волн, которые образуются в столбе воздуха, заключенного внутри закрытой с обоих концов узкой, длинной трубы. В таких трубах в определенном диапазоне частот звуковые волны близки к плоским, что существенно упрощает расчеты. 2. Основные понятия 2.1.Звуковые волны в газах и жидкостях являются продольными: колебания частиц среды происходят вдоль направления распространения волны. Пусть в газе вдоль оси OХ распространяется плоская продольная гармоническая волна смещений 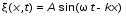 , (1) , (1)где А - амплитуда смещений; 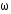 - циклическая частота, - циклическая частота,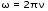 ; V- линейная частота; K- волновое число; ; V- линейная частота; K- волновое число; 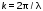 , , 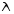 - длина волны. - длина волны.Рассмотрим элементарный объем газа в виде цилиндра с площадью сечения S и длиной x, его объем W = Sx. При прохождении волны (1) этот объем подвергается смещению и деформации (рис. 1). 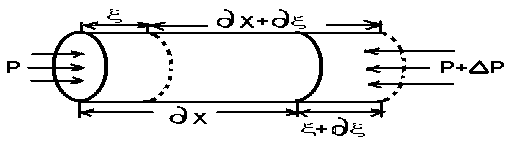 Рис.1 Изменение объема газа ∆W = S приводит к изменению давления в нем на ∆P по сравнению с давлением P, которое существует в газе в отсутствие волны. В звуковой волне сжатия и расширения газа следуют друг за другом так быстро, что смежные участки среды не успевают обмениваться теплом. Такие процессы в термодинамике называются адиабатическими. В этом случае связь между давлением P и объемом W данной массы газа выражается уравнением 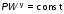 , (2) , (2)где γ - показатель адиабаты, значение которого зависит от вида газа. Логарифмируя (2) и затем дифференцируя полученное выражение, можно получить соотношение для относительных изменений давления и объема 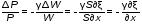 . (3) . (3)Дифференцируя (1) по х и подставляя в (3), получим 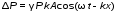 . (4) . (4)Величина 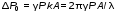 называется амплитудой избыточного (звукового) давления. Для обычных звуковых волн (кроме ударных) амплитуда смещений много меньше длины волны (А << λ), поэтому P0 << P. называется амплитудой избыточного (звукового) давления. Для обычных звуковых волн (кроме ударных) амплитуда смещений много меньше длины волны (А << λ), поэтому P0 << P.Таким образом, звуковая волна в газе с термодинамической точки зрения представляет собой волну избыточного давления, изменяющуюся по закону 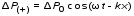 , (5) , (5)которая распространяется в положительном направлении оси OХ со скоростью 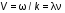 . .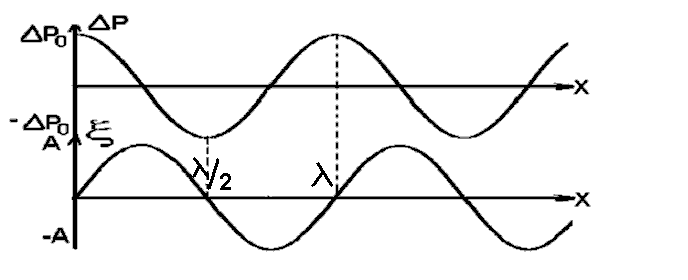 Рис.2 На рис. 2 изображены "профили" волн избыточного давления и смещений в момент времени t = 0. Из рисунка видно, что нули смещений соответствуют максимумам (минимумам) избыточного давления. Уравнение волны избыточного давления, распространяющейся вдоль отрицательного направления оси OX, получается заменой х на –х в (5) 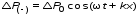 . .2.2. Стоячая волна образуется в результате наложения (интерференции) двух гармонических волн, распространяющихся навстречу друг другу. Уравнение стоячей волны избыточного давления (при равенстве амплитуд) имеет вид 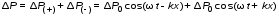 или, преобразовав, 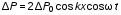 . (6) . (6)Из уравнения (6) следует, что в стоячей звуковой волне существуют точки, в которых избыточное давление постоянно равно нулю. Такие точки называются узлами, их координаты определяются из условия coskx = 0 или xуз = (m + 1/2)λ/2, (m = 0, 1, 2 ...). (7) Точки, для которых |coskx|=1, амплитуда колебаний избыточного давления максимальна и равна 2∆P0, называются пучностями. Координаты пучностей определяются по формуле xпуч = mλ/2, (m= 0, 1, 2 ...). (8) Из (7) и (8) видно, что расстояние между двумя соседними узлами (пучностями) равно λ/2, а расстояние между соседним узлом и пучностью равно λ/4. 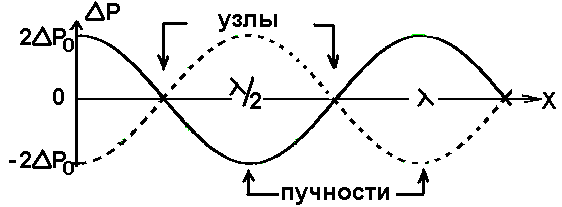 Рис. 3 На рис. 3 изображены "профили" стоячей волны звукового давления в различные моменты времени: сплошной линией при t = 0, пунктиром - при t= Т/2. 2.3. На практике стоячие волны чаще всего образуются при наложении прямой волны и волны, отраженной от какого-либо "препятствия". При распространении звуковых волн в трубах такими "препятствиями" могут служить либо закрытый, либо открытый торцы трубы. Поэтому "профили" стоячих волн, которые могут возбуждаться в столбах газа в трубах, определяются условиями на торцах трубы - граничными условиями: 1) на открытом конце трубы всегда возникает узел звукового давления (так как на открытом торце труба соседствует с атмосферой) или пучность смещений (так как частицы могут свободно смещаться); 2) на закрытом конце трубы образуется пучность звукового давления (так как скачок давления возможен лишь на закрытом конце трубы) или узел смещений (так как частицы вблизи стенки не могут смещаться). 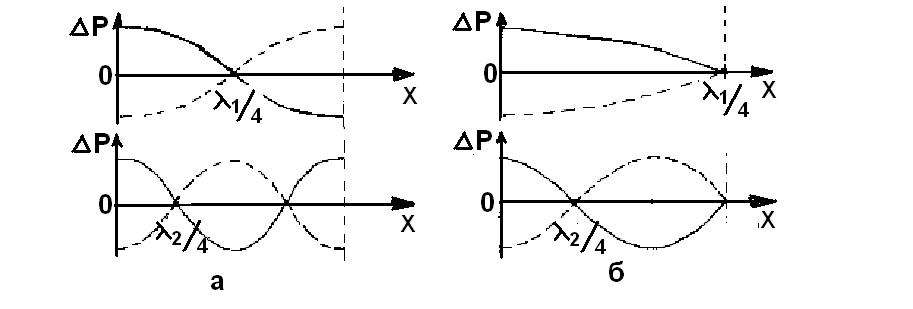 Рис. 4 На рис. 4,а показаны распределения звукового давления в закрытой с обоих концов трубе, удовлетворяющие граничным условиям (2) для первых двух видов стоячих волн-гармоник. Пунктиром дан вид распределения через полпериода. Для сравнения на рис. 4,б представлены соответствующие распределения для полузакрытой трубы (граничные условия: при х = 0 - пучность, при х = L - узел). 2.4. Частоты, соответствующие возможным при данных граничных условиях стоячим волнам, называются собственными (нормальными) частотами. Для того чтобы найти собственные частоты для закрытой трубы, сравним рис. 3 и 4,а: для первой гармоники (основной тон) - L = λ1 / 2, для второй (первый обертон) L = 2λ2 / 2, для третьей (второй обертон) L = 3λ3 / 2 и т.д. В общем случае L = nλn/ 2 , где n = 1, 2, 3, ... Отсюда λn = 2 L / n. (9) Собственные частоты соответствующих гармоник 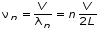 . (10) . (10)2.5. В лабораторной установке площади микрофона и динамика существенно меньше площади торцов трубы, поэтому ее можно считать закрытой с обоих концов (см. рис. 4, а). При возбуждении звука в закрытой трубе в ней возникают резонансы на собственных частотах, определяемых соотношением (10), причем разность частот двух соседних резонансов постоянна и равна 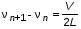 . (11) . (11) Отсюда по известным 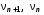 и L можно найти скорость распространения звука и L можно найти скорость распространения звука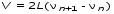 . (12) . (12)2.6. Переход от одной гармоники к другой может быть также осуществлен путем изменения резонансной длины трубы L при фиксированной частоте и, следовательно, при фиксированной длине звуковой волны 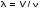 . Из соотношений (9), (10) и рис. 4,а следует, что изменение d длины трубы L между двумя соседними ее резонансами равно λ/2, т.е. . Из соотношений (9), (10) и рис. 4,а следует, что изменение d длины трубы L между двумя соседними ее резонансами равно λ/2, т.е. 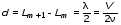 . (13) . (13)2.7. Скорость звуковых волн в газах зависит от равновесных значений давления P и температуры Т. Для идеальных газов в адиабатическом приближении теоретическое значение скорости звука можно вычислить по формуле (см. приложение) 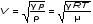 , (14) , (14) где γ - показатель адиабаты (γ = 1,4 для воздуха); р, ρ - равновесные значения давления и плотности; μ - молярная масса ; μ возд. = 0,029 кг/моль; R = 8,31 Дж/(мольК) - универсальная газовая постоянная; Т - абсолютная температура. Подставляя значения постоянных, можно получить приближенную формулу 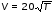 (м/с). (15) (м/с). (15)3. Описание лабораторной установки 3.1. Схема экспериментальной установки для определения скорости звука в воздухе методом стоячих волн приведена на рис. 5. Установка состоит из металлической трубы Т, внутри которой на заглушках укреплены динамик D и микрофон М. Заглушка с динамиком может перемещаться внутри трубы с помощью штанги Ш, на которой нанесена шкала отсчета. К динамику подводится напряжение звуковой частоты от генератора ЗГ. Звуковые сигналы, преобразованные микрофоном в электрические, подаются через усилитель У на вход осциллографа ЭО. 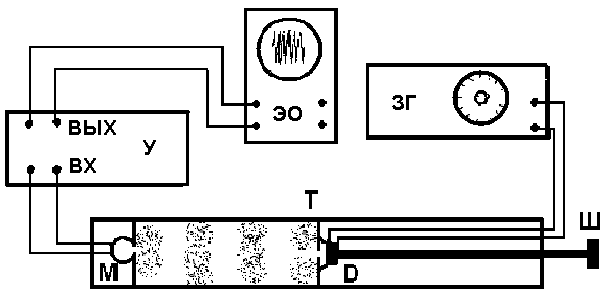 Рис. 5 Рекомендуемый диапазон частот для работы с данной трубой (2000…4000 Гц) выбран с целью получения звуковых волн, близких к плоским. 3.2. Техника безопасности Корпуса осциллографа, генератора и усилителя должны быть заземлены. Запрещается включать приборы без разрешения преподавателя или лаборанта. 4. Порядок измерений 4.1. Внести технические данные приборов в табл.1. Таблица 1
4.2. Упражнение 1 4.2.1. Включите генератор ЗГ, усилитель У и осциллограф ЭО. Переместите динамик на минимальное расстояние L0 от микрофона. Его значение, указанное на установке, внесите в табл. 2. 4.2.2. Переключатель "ослабление" ЗГ поставьте в положение "0,1 V", а ручкой "регулировка выхода" ЗГ подберите такую амплитуду звукового сигнала, чтобы на экране ЭО наблюдался сигнал размахом в несколько сантиметров. 4.2.3. Изменением частоты выберите два соседних резонанса, соответствующих n-й и (n +1)-й гармоникам в диапазоне частот 2000 … 4000 Гц. Значения этих частот занесите в табл. 2. Таблица 2 L0 = м
4.3. Упражнение 2 4.3.1. Установите на звуковом генераторе частоту, соответствующую более сильному резонансу. Занесите значения выбранной частоты в табл. 3. 4.3.2. Постепенно выдвигая динамик, фиксируйте его положения, соответствующие максимуму сигнала. Данные занесите в табл. 3. Таблица 3 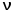 = Гц = Гц
5. Обработка результатов измерений 5.1. Вычислите значение скорости звука для упражнения 1 по формуле 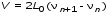 . .5.2. Определите приборные погрешности (относительную и абсолютную) 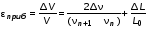 . .5.3. Представьте окончательный результат в виде 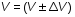 , м/c. , м/c.5.4. Вычислите среднее значение скорости звука в воздухе для упражнения 2 по формуле 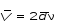 . .5.5. Определите относительную приборную погрешность 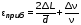 . .5.6. Определите случайную погрешность 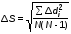 ; ;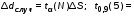 2,1; 2,1;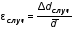 . .5.7. Найдите полные относительную и абсолютную погрешности 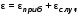 ; ;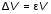 . .5.8. Представьте окончательный результат в виде 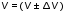 , м/c. , м/c.5.9. По формуле (15), зная комнатную температуру, рассчитайте теоретическое значение скорости звука в воздухе. Сравните это значение с результатами предыдущих вычислений. Литература 1. Савельев, И.В. Курс общей физики. T.4. Волны. Оптика / И.В.Савельев.- М.: Изд-во « Астрель», 2001. Приложение Для вывода формулы скорости звука в воздухе воспользуемся уравнением движения массы газа, заключенного в элементарном объеме W = Sx ( рис. 1) 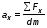 . (16) Масса газа, заключенного внутри W, равнаdm = ρSx; ее ускорение ax=2/t2; результирующая сила вдоль оси OХ . (16) Масса газа, заключенного внутри W, равнаdm = ρSx; ее ускорение ax=2/t2; результирующая сила вдоль оси OХ 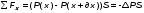 или, учитывая (3), или, учитывая (3), 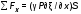 . .Подставляя эти выражения в (16), получим 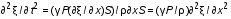 . (17) . (17) Сравнивая (17) с дифференциальным волновым уравнением (2/t2 = V22/x2), для скорости распространения звука в газе получим формулу 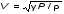 или или 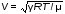 , учитывая что , учитывая что 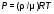 . .Вопросы для самоконтроля 1-й комплект 1. Покажите, что стоячая волна (x,t) = A cos(kx)· cos(ωt) удовлетворяет волновому уравнению 2/t2 = V22/x2. 2. Нарисуйте профили бегущей волны смещений аналогично рис.2, в моменты времени t = 0, Т/4, Т/2. 3. Вычислите значение минимальной частоты стоячей волны в данной трубе при её длине, равной L0. 2-й комплект 1. Запишите уравнение плоской гармонической волны и укажите ее параметры. 2. Нарисуйте профили стоячей волны звукового давления (рис. 3) в момент времени t = 0, Т/4, Т/2. 3.Определите номера гармоник, возбуждаемых при выполнении данной лабораторной работы на частотах 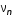 и и 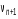 (упражнение 1). (упражнение 1).3-й комплект 1. Дайте определение продольным и поперечным упругим волнам, укажите условия их распространения в твердых, жидких и газообразных средах. 2. Покажите направления скоростей частиц газа 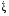 = /t в бегущей волне в точках х = 0, /2, (рис. 2) в моменты времени t = 0 и t = Т/2. = /t в бегущей волне в точках х = 0, /2, (рис. 2) в моменты времени t = 0 и t = Т/2.3. Найдите отношение частот первой и третьей гармоник в полузакрытой трубе (рис. 4,б). 4-й комплект 1. Выведите уравнение стоячей волны звукового давления и укажите положения узлов и пучностей, формулы (7) и (8). 2. Объясните физический смысл граничных условий для смещения частиц и звукового давления. 3. Найдите частоту основного тона столба воздуха в закрытой трубе длиной L = 1 м. Как изменится эта частота, если труба будет заполнена гелием ( 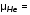 0,004кг/моль), углекислым газом ( 0,004кг/моль), углекислым газом (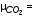 0,044 кг/моль)? 0,044 кг/моль)?5-й комплект 1. Сформулируйте принцип суперпозиции волн. 2. В момент времени t = Т/4 звуковое давление в стоячей волне равно нулю при любом х, см. уравнение (6). Поясните причину появления звукового давления в соседние моменты времени. 3. Как будет изменяться частота основного тона закрытой трубы, если ее сначала открыть с одного конца, а потом с другого? 6-й комплект 1. Стоячая волна является частным случаем явления интерференции. Поясните. 2. Выразите связь граничных условий для смещений частиц и звукового давления (рис 4, а, б). 3. В упражнении 1 учитывается и вычисляется только приборная погрешность, а в упражнении 2 - приборная и случайная. Почему? Описание работы написали и составили вопросы для самоконтроля ст. преподаватели Афанасьев Б.Л и Гусева Е.А. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

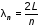
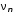 ,Гц
,Гц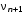 ,Гц
,Гц 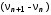 , Гц
, Гц