Колебания и волны. Лабораторная работа 2к определение параметров физического маятника Введение
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
Лабораторная работа № 12-К«ИЗУЧЕНИЕ ИНТЕРФЕРЕНЦИИ СВЕТА»1. Введение1.1. Радужная окраска нефтяных и масляных пятен на поверхности воды, цвета побежалости на закаленных металлах, сиреневый оттенок объектива фотоаппарата – эти и многие другие явления объясняются интерференцией света.Явление интерференции имеет самое широкое применение для измерения длины волны излучения, определения толщины пленок, плотности, показателя преломления и дисперсионных свойств веществ, для контроля качества поверхности, при просветлении оптики и т. д. 1.2. Целью работы является изучение интерференции световых волн методом колец Ньютона и определение радиуса кривизны линзы. 2. Основные понятия2.1. Интерференцией называется явление перераспределения световой энергии при наложении когерентных волн, в результате которого возникают максимумы и минимумы интенсивности. Когерентными называются волны с постоянной во времени разностью фаз. 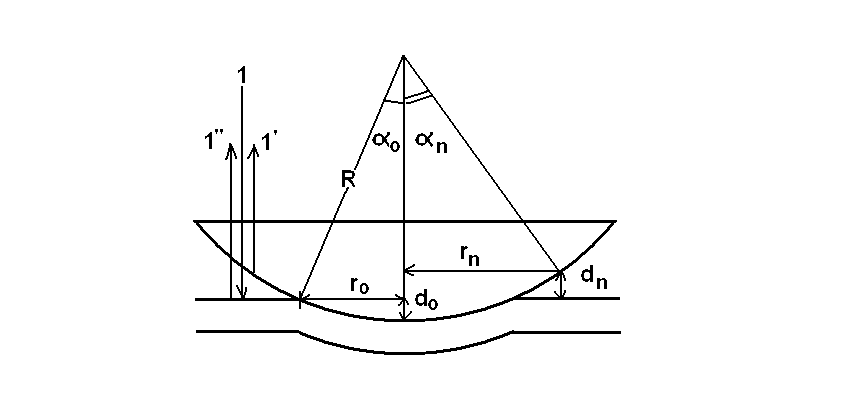 Рис. 1 В интерференционных схемах когерентные волны получают путем искусственного разделения светового потока, исходящего из одного источника, на две или более частей. В данной работе монохроматический параллельный пучок света падает нормально на установку, состоящую из стеклянной плосковыпуклой линзы и плоскопараллельной пластины (рис. 1). При наложении лучей света 1' и 1'', отраженных соответственно от верхней и нижней границ тонкой воздушной прослойки, находящейся между поверхностью пластинки и соприкасающейся с ней выпуклой сферической поверхностью линзы, наблюдается интерференционная картина. Геометрическая разность хода лучей 1' и 1'' равна удвоенной толщине воздушной прослойки в месте падения лучей. Поскольку луч 1'' отражается от оптически более плотной среды, фаза отраженной волны меняется на , что эквивалентно дополнительной разности хода лучей, равной /2. В результате оптическая разность хода лучей 1' и 1'' равна (см. рис. 1) 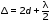 . (1) . (1)Если оптическая разность хода интерферирующих волн составляет нечетное число полуволн, наблюдается ослабление света (min интерференции) 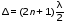 . (2) . (2)Усиление света (max интерференции) происходит, если оптическая разность хода составляет целое число длин волн 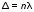 , (3) , (3)где n порядок интерференции (n = 0, 1, 2...). Интерференционные максимумы и минимумы соответствуют определенным толщинам воздушной прослойки, образуя интерференционные полосы равной толщины, которые в данном случае имеют вид чередующихся темных (min) и светлых (max) концентрических колец колец Ньютона. Условие образования n-го темного кольца с учетом (1) и (2) запишется так: 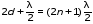 . (4) . (4)2.2. При освещении установки белым светом интерференционные кольца окрашены. Число наблюдаемых колец невелико, так как происходит наложение колец разных длин волн, и они расплываются. 2.3. Вследствие деформации контакт линзы с пластиной осуществляется не в одной точке. В результате центральное (нулевое) темное пятно имеет относительно большие размеры. Так как обычно используется тонкая пластинка, то деформируется (прогибается) в основном она. Это изображено на рис.1, где 2r0 диаметр центрального темного пятна. Приближенно считая остальную часть стеклянной пластинки недеформированной, можно рассчитать радиус кривизны линзы R, измерив радиусы нескольких темных колец. Из рис.1 следует, что глубину деформации пластины d0 можно выразить как 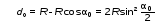 . (5) . (5) Учитывая малость углов, имеем 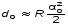 , (6) , (6)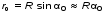 . (7) . (7)Решая совместно (6) и (7), получаем 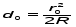 . (8) . (8)Толщины воздушных прослоек находим из выражения (4)  . (9) . (9) Далее, аналогично (6),(7) и (8) 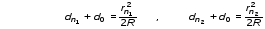 . (10) . (10)Решая совместно (8), (9) и (10), получаем расчетную формулу для радиуса кривизны линзы 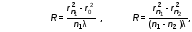 (11) (11)где r0 радиус центрального темного пятна; rn1 и rn2 радиусы темных колец с соответствующими номерами; длина волны излучения. 2.4. Эксперимент заключается в получении интерференционной картины и измерении радиусов двух темных колец. Дальнейшая обработка результатов измерений позволяет вычислить радиус кривизны линзы R и его погрешность. |
