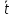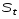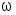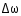Колебания и волны. Лабораторная работа 2к определение параметров физического маятника Введение
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
|
Вопросы для самоконтроля 1-й КОМПЛЕКТ 1. Какие колебания называются свободными? Чем определяется частота их колебаний? 2. Из каких законов физики получается дифференциальное уравнение свободных колебаний в электромагнитном контуре? 3. Какие величины для механического осциллятора аналогичныi, L, C? 2-й КОМПЛЕКТ 1. Какими двумя независимыми способами можно вызвать свободные колебания в электромагнитном контуре? 2. Напишите дифференциальное уравнение затухающих колебаний. Его решение при ω0 > β. 3. Сколько колебаний совершится за время релаксации t = 1/β? 3-й КОМПЛЕКТ 1. По аналогии с чем колебания в контуре в некоторых случаях называют ударными? 2. Как найти A0 из начальных условий при малом затухании ? 3. Что такое r0, где оно находится? 4-й КОМПЛЕКТ 1. Запишите решение дифференциального уравнения в случае критического затухания. Найдите a1и a2, если q (0) = 0, i(0) = E / R. 2. Дайте определение логарифмического декремента затухания, добротности. 3. В какой системе двигателя внутреннего сгорания встречаются собственные электромагнитные колебания? 5-й КОМПЛЕКТ 1. Назовите основные параметры затухающих колебаний. 2. Проведите аналогию между пружинным маятником и электро-магнитным контуром. 3. Зачем в подвеске автомобиля применяются амортизаторы? 6-й КОМПЛЕКТ 1. Какими элементами контура определяются ω0, β? 2. Не противоречит ли формула (17) формуле (6) для расчета логарифмического декремента затухания λ ? 3. Чему аналогична сила упругости пружины для электромагнитного контура? 7-й КОМПЛЕКТ 1. Оцените, на сколько процентов отличаются ω0 от частоты затухающих колебаний, если добротность системы Q= 10 . 2. Что такое начальные условия? Дайте их толкование с энергетической точки зрения. 3. Как по осциллограмме, рис.10,(Г), оценить добротность контура? 8-й КОМПЛЕКТ (для тех, кто немного знает радиотехнику) 1. Зачем нужен диод в схеме ключа (рис.8) и можно ли обойтись без него (рис. 6)? 2. Почему в формуле (10) у тока i0 стоит знак – (минус). Как это отражается на осциллограмме, рис.10,(Г)? 3. Докажите справедливость формулы (9). 9-й КОМПЛЕКТ(для тех, кто немного знает радиотехнику) 1. На схеме электронного зажигания с коммутатором, рис.18,(2), отсутствует конденсатор. Как же без него оно работает? 2. Какой вид будет иметь осциллограмма рис.9,(В), если сопротивление Rочень велико? 3. Объясните работу транзистора в роли ключа (рис.6). 10-й КОМПЛЕКТ (для тех, кто немного знает радиотехнику) 1. Разберитесь в первом варианте схемы искрового зажигания. Изобразите осциллограммы напряжения на конденсаторе и тока в первичной обмотке катушке зажигания. 2. Если не известна ёмкость конденсатора в контуре, как можно было бы оценить её значение с помощью лабораторной установки? 3. Как влияет наличие сердечника на индуктивность катушки? Лабораторную работу поставил, написал описание и составил вопросы для самоконтроля ст. преподаватель Афанасьев Б.Л. Лабораторная работа № 4-К «ИЗУЧЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ В ЭЛЕКТРОМАГНИТНОМ КОНТУРЕ» 1. Введение Колебательная система совершает вынужденные колебания под действием внешнего периодического воздействия, которым может быть механическая сила, ЭДС, электромагнитное поле. Изучая поведение системы при изменении частоты внешнего воздействия, оказывается возможным получить исчерпывающие сведения о её свойствах, будь то механическая или электромагнитная система. Данная лабораторная работа посвящена экспериментальному ознакомлению с вынужденными колебаниями в электромагнитном контуре. 2. Основные понятия
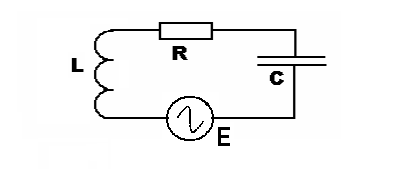 Рис.1 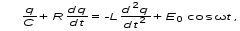 (1) (1) где q – величина заряда на емкости, dq/dt = i – сила тока, - Ldi/dt - ЭДС самоиндукции. Введя, как обычно: β = R/2L – коэффициент затухания , ω0 = 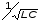 - круговую частоту собственных незатухающих колебаний , получим из (1) дифференциальное - круговую частоту собственных незатухающих колебаний , получим из (1) дифференциальноеуравнение в виде 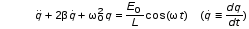 . (2) . (2) При малом затухании (β < ω0) решение неоднородного дифференциального уравнения (2) имеет вид 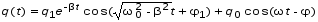 , (3) , (3) где первое слагаемое отвечает собственным затухающим колебаниям, а второе – вынужденным. После окончания переходного процесса установятся вынужденные колебания 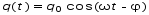 , (4) , (4) происходящие с частотой вынуждающей ЭДС ω . Амплитуду вынужденных колебаний и сдвиг фаз φ между колебаниями заряда и вынуждающей ЭДС можно найти методом векторных диаграмм (см. литературу). Зависимости qo(ω) и φ (ω) называются амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристиками и имеют вид 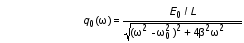 , (5) , (5) 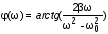 . (6) . (6) 2.2. АЧХ имеет максимум на частоте 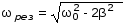 , (7) , (7) называемой резонансной. При этом отношение максимальной амплитуды заряда 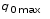 к амплитуде заряда при малых частотах к амплитуде заряда при малых частотах 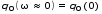 будет равно будет равно 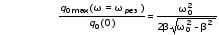 , (8) тогда при β<<ω0 , (8) тогда при β<<ω0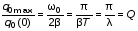 , (9) , (9)где Q – добротность контура. 2.3. Проанализируем поведение АЧХ в области резонансной частоты при малом затухании. Здесь можно считать ω ≈ ω0 , тогда 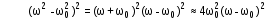 . .Подставляя это выражение в формулу (5), получим 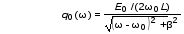 (10) (10) - уравнение АЧХ при малых расстройках. Такой вид зависимости (или, как говорят, резонансный отклик) характерен для большинства колебательных систем независимо от их физической природы. Найдём значения частот, при которых q0(ω) в √2 раз меньше максимального значения 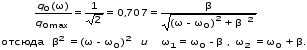 ; (11) ; (11)Разность этих значений частоты называется полосой пропускания на уровне 0,7 (от максимального) 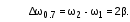 (12) 2.4. Так как напряжение на ёмкости UC = q / C, все перечисленные закономерности относятся и к АЧХ напряжения UC. Из формул (4), (5), (7), (8), (9) и (12) получим 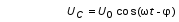 , (13) , (13)где U0= q0/C - амплитуда напряжения. При ω ≈ 0,  U0(0) = E0 . U0(0) = E0 . При ω = ωрез ,U0max = QE0.(14) Также 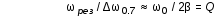 . (15) . (15)2.5. В лабораторной работе необходимо получить АЧХ напряжения на ёмкости, снимая зависимость амплитуды напряжения U0 от частоты 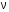 вынуждающей ЭДС, построить АЧХ (резонансную кривую); определить резонансную частоту, полосу пропускания, рассчитать добротность Q и, зная ёмкость конденсатора С, найти индуктивность контура L и его активное сопротивление R. вынуждающей ЭДС, построить АЧХ (резонансную кривую); определить резонансную частоту, полосу пропускания, рассчитать добротность Q и, зная ёмкость конденсатора С, найти индуктивность контура L и его активное сопротивление R.3. Описание лабораторной установки 3.1. Лабораторная установка состоит из генератора звуковых частот ГЗ-33, платы контура и вольтметра V , измеряющего напряжение на конденсаторе (рис. 2). 4. Техника безопасности 4.1. Перед началом работы убедитесь в наличии заземления корпуса генератора. 4.2. Проводить лабораторную работу только под руководством преподавателя или лаборанта. 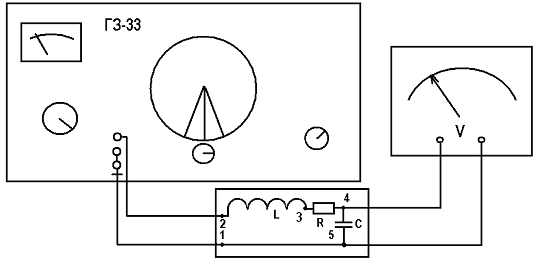 Рис.2 5. Порядок выполнения работы 5.1. Запишите значение ёмкости контура в табл. 1. Туда же внести технические данные приборов. Таблица 1
5.2 . Снятие АЧХ 5.2.1.Собрать электрическую схему согласно рис.2. После проверки схемы преподавателем включить генератор в сеть 220 В. 5.2.2. Дать прогреться генератору 3…5 минут. Установить выходное сопротивление генератора равным 5 Ом. Ступенчатым регулятором выходного напряжения установить его в пределах 1…3 В. Изменяя частоту генератора (ступенчато и плавно), найти резонанс по максимальному показанию вольтметра. Затем, плавно изменяя выходное напряжение, добиться того, чтобы оно равнялось точно 10,0В. Записать резонансную частоту 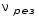 и напряжение Uomax в табл. 2. и напряжение Uomax в табл. 2.5.2.3. Плавно изменяя частоту генератора, измерить напряжение в 7...10 точках ниже резонансной частоты и также в 7…10 точках выше неё. Пределы изменения частоты выбрать такими, чтобы напряжение на конденсаторе уменьшалось примерно до 2…3 В. Можно снять АЧХ по-другому, задавая частоты такими, чтобы напряжение проходило ряд целых значений 2,3,4,5,6,7,8,9,10,9,8,7,6,5,4,3,2,1 В. Данные записать в табл. 2. 5.2.4. Установить частоту генератора, в 10 раз меньшую резонансной (ступенчатым регулятором). В этом случае U0( 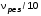 ) ≈ U0(0). Полученные результаты также поместить в табл. 2 ) ≈ U0(0). Полученные результаты также поместить в табл. 2
Таблица 2. 6. Обработка результатов измерений 6.1. По данным табл. 2 построить на миллиметровой бумаге график АЧХ. 6.2. Проведя прямую на уровне 0.7 U0max , найти полосу пропускания 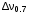 (рис.3). (рис.3).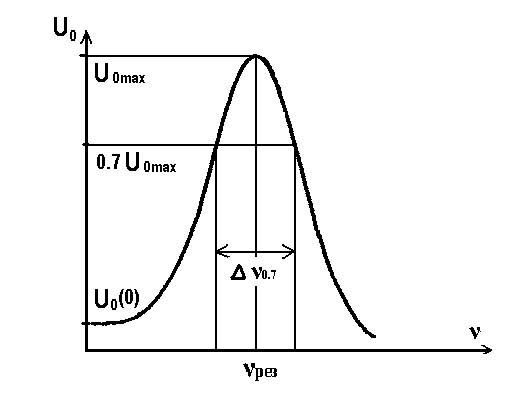 Рис.3 6.3. Так как обычные частоты 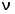 и круговые ω связаны соотношением и круговые ω связаны соотношением 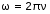 , то , то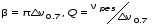 . (16) . (16) 6.4. Используя значения 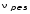 , ,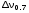 , U0max, U0(0), C, а также погрешности установки частоты ∆ , U0max, U0(0), C, а также погрешности установки частоты ∆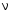 и измерения напряжения ∆U0, рассчитать добротность контура Q, его индуктивность L, сопротивление R , а также относительные погрешности этих величин и измерения напряжения ∆U0, рассчитать добротность контура Q, его индуктивность L, сопротивление R , а также относительные погрешности этих величин 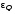 и и 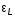 . Результаты поместить в табл. 3. . Результаты поместить в табл. 3.Таблица 3
Литература
Вопросы для самоконтроля 1-й КОМПЛЕКТ 1. Какие колебания называются вынужденными? Чем определяется частота их колебаний? 2. Каков физический смысл добротности? Как она проявляется в вынужденных колебаниях? 3. Вывести формулу для расчета индуктивности из табл. 3. 2-й КОМПЛЕКТ 1. Что такое резонансная частота? Вывести формулу (7). 2. В чём состоит отличие резонанса в контуре с большой и малой добротностью? 3. Будут ли проявляться резонансные явления в контуре, если затухание в нём больше или равно критическому (ω0<β, ω0 = β)? 3-й КОМПЛЕКТ 1. Запишите дифференциальное уравнение вынужденных колебаний в электромагнитном контуре. Из каких законов физики оно получается? 2. Что такое полоса пропускания контура? От каких параметров она зависит? 3. Где в бытовой технике используется явление резонанса? 4-й КОМПЛЕКТ 1. Запишите общее решение дифференциального уравнения вынужденных колебаний. Из каких частей оно состоит? 2. Как рассчитать добротность по полосе пропускания? Разберитесь с выводом формул (10), (11), (12). 3. Какой величине для механического осциллятора аналогична внешняя ЭДС? 5-й КОМПЛЕКТ 1. Какой смысл имеют величины ω0 , β , ω? 2. Проведите аналогию между вынужденными колебаниями в электромагнитном контуре и механическими вынужденными колебаниями. 3. В чём заключается переходный процесс? Что наблюдается после его окончания? 6-й КОМПЛЕКТ 1. Что такое АЧХ? Каков её график? 2. Выразите добротность контура Q через его параметры R, L, C. 3. Каким величинам для механического осциллятора аналогичны q , i , Uc= q/C ? Лабораторную работу поставил, написал описание и составил вопросы для самоконтроля ст. преподаватель Афанасьев Б.Л. Лабораторная работа № 7-К «ИЗУЧЕНИЕ СОБСТВЕННЫХ КОЛЕБАНИЙ МЕХАНИЧЕСКИХ СИСТЕМ» 1. Введение 1.1. Пружинный маятник является одним из самых простых и важных для технических приложений примеров осциллятора – системы способной совершать собственные (при некоторых условиях близкие к гармоническим) колебания. 1.2. Целью настоящей лабораторной работы является экспериментальное ознакомление с собственными колебаниями пружинного маятника и определение некоторых его параметров. 2. Основные понятия 2.1. Дифференциальное уравнение, описывающее динамику одномерных затухающих колебаний пружинного маятника (рис.1), при наличии сил сопротивления пропорциональных скорости (движение с небольшими скоростями в газе или жидкости), можно записать на основе законов Ньютона, Стокса и Гука в следующем виде: 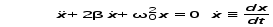 , (1) , (1) ω0= 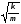 , (2) , (2)где x(t) – смещение маятника от положения равновесия,β = r / 2m - коэффициент затухания; ω0 - круговая частота собственных незатухающих колебаний , m – масса груза, r – коэффициент сопротивления, k – коэффициент упругости пружины. 2.2. Решение этого уравнения при малом затухании (β < ω0) получаем в виде затухающих колебаний- график на рис.(1): 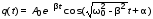 . (3) . (3) Начальные амплитуда А0 и фаза α определяются начальными смещением и скоростью  . .2.3. Для характеристики степени затухания, кроме величины β, используют логарифмический декремент затухания λ - он равен натуральному логарифму отношения двух последующих амплитуд (отличающихся по времени на период T) 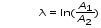 . (4) Из формул (3) и (4) следует . (4) Из формул (3) и (4) следует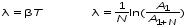 , (5) , (5) где N – число колебаний, совершенных между измерениями амплитуд. 2.4. В процессе колебаний энергия упругой деформации пружины переходит в кинетическую энергию груза и наоборот. Эти переходы сопровождаются потерями. Удобно пользоваться добротностью осциллятора Q, которая вводится как 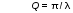 . (6) . (6)Можно показать, что при достаточно малом затухании (β <<ω0) 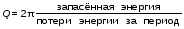 . (7) . (7)2.5. В данной лабораторной работе нужно определить собственную частоту незатухающих колебаний статическим методом, частоту затухающих колебаний динамическим методом, рассчитать логарифмический декремент затухания и добротность. 3. Описание лабораторной установки 3.1. Общий вид лабораторной установки показан на рис.1. Изучается затухание колебаний в воздухе. Растяжение пружины и амплитуды колебаний определяется по измерительной линейке Л с помощью измерительного диска Д. Время колебаний определяется ручным секундомером. 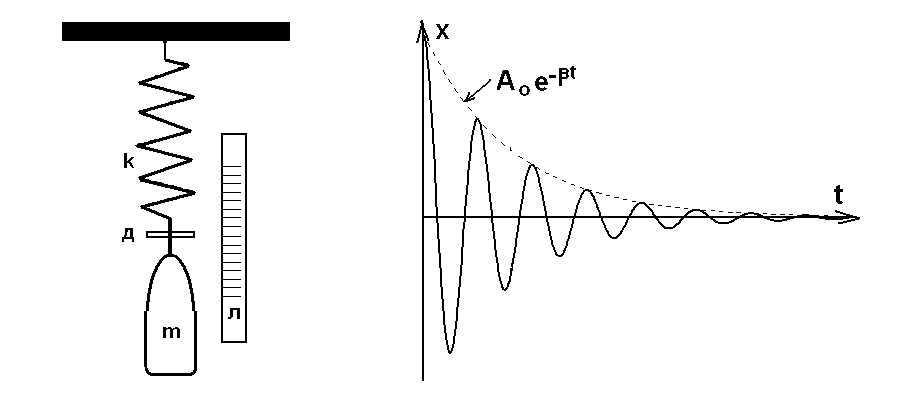 Рис.1 4. Техника безопасности 4.1. При проведении работы соблюдайте правила техники безопасности. 4.2. Бережно относитесь к оборудованию и измерительным приборам. 5. Порядок выполнения работы и обработка результатов измерений 5.1. Запишите технические данные приборов в табл. 1. Таблица 1
5.2. Определение собственной частоты незатухающих колебаний статическим методом. 5.2.1. Измерив статическое удлинение пружины x под действием груза массы m, имеем (из kx = mg) k = mg /x; подставляя в формулу (2), получим 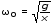 (8) (8) 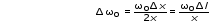 , (9) , (9) где Δl – погрешность линейки. Данные поместить в табл. 2. Таблица 2
Записать результат вычисления частоты в виде ω0 = (ω0 ± Δω0), 1/c 5.3. Измерение частоты затухающих колебаний динамическим методом 5.3.1. Измерив 5 раз секундомером время t десяти полных периодов колебаний маятника, можно рассчитать период колебаний и их частоту, с погрешностями, по приведённым формулам (10),(11): 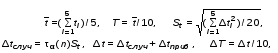 (10) (10)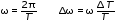 . (11) . (11)Данные поместить в табл. 3 и 4. Таблица 3
Таблица 4 Записать результат расчёта частоты в виде ω = (ω ± Δω),1/c. Cравнить с данными по ω0. 5.4. Расчёт логарифмического декремента затухания колебаний и добротности пружинного маятника 5.4.1. Задав начальную амплитуду (оттянув маятник вниз от положения равновесия на 20 мм и отпустив), отсчитывают наглядно число Nполных колебаний маятника за время уменьшения их амплитуды в 2 раза. Измерение провести один раз. Рассчитать логарифмический декремент λ и добротность Q по формулам (5) и (6) с погрешностями (учитывая только приборные) 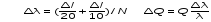 , (12) где Δl - приборная погрешность линейки в мм. Данные поместить в табл. 5. , (12) где Δl - приборная погрешность линейки в мм. Данные поместить в табл. 5. Таблица 5
Записать результаты расчёта в виде λ = λ ± Δλ Q = Q ± ΔQ. Литература 1.Савельев, И.В. Курс общей физики. Т.1. Механика / И.В.Савельев.- М.: Изд-во « Астрель», 2001. 2. Савельев, И.В. Курс общей физики. T2. Электричество и магнетизм / И.В.Савельев.- М.: Изд-во «Астрель», 2001. Вопросы для самоконтроля 1-й КОМПЛЕКТ 1. Из каких законов физики и как выводится уравнение (1)? 2. Выразите начальную амплитуду (при малом затухании), исходя из начальных условий x0 = 0.1м V0= 0 . 3. Чему равно относительное изменение амплитуды за один период, если λ <<1? 2-й КОМПЛЕКТ 1. Назовите основные параметры затухающих колебаний. 2. Запишите дифференциальное уравнение затухающих колебаний. Его решение при ω0 > β. 3. Сколько колебаний совершится за время релаксации τ =1 / β ? 3-й КОМПЛЕКТ 1. Покажите, что формула для добротности Q (7) приводит к формуле (6). При каких условиях? 2. Найти A0 из начальных условий при малом затухании (x0 = 0 , V0= 1 м/c, ω0 =10 1/c). 3. Покажите линейную зависимость ускорения от смещения при гармонических колебаниях. 4-й КОМПЛЕКТ 1. Запишите решение дифференциального уравнения-формула (1). Приведите его график (ω0 > β). 2. Дайте определение логарифмического декремента затухания, добротности. 3. Докажите эквивалентность формул (4) и (5). 5-й КОМПЛЕКТ 1. При каких условиях совершаются колебания близкие к гармоническим? 2. Проведите аналогию между пружинным маятником и электромагнитным контуром. 3. Как изменится амплитуда за период, если λ= 0.1? 6-й КОМПЛЕКТ 1. Выведите формулу для частоты собственных гармонических колебаний тела, подвешенного на пружинке. 2. Что такое время релаксации? От каких параметров оно зависит? 3. Чему аналогична сила упругости пружины для математического маятника? Написал описание лабораторной работы и составил вопросы для самоконтроля ст. преподаватель Афанасьев Б.Л Лабораторная работа № 10-К «Исследование нормальных колебаний струны» 1. Введение Распространение в пространстве различных возмущений состояния вещества или поля называется волновым процессом или волной. Примерами волн являются звук (упругие волны) и свет (электромагнитные волны). Довольно часто наблюдаются стоячие волны, образующиеся в результате сложения падающих и отраженных волн. Так, например, каждый тон звучания музыкальных инструментов является стоячей волной струны или столба воздуха. На приемной антенне телевизора и в рабочем объеме лазера устанавливаются стоячие электромагнитные волны. В настоящей работе изучаются нормальные колебания струны, являющиеся стоячими упругими волнами. 2. Основные понятия 2.1. Уравнение гармонической плоской волны, распространяющейся вдоль оси OX , имеет вид 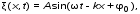 (1) (1)где 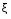 - смещение частиц от положения равновесия; - смещение частиц от положения равновесия;A - амплитуда колебания; к - волновое число, равное 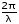 , где , где 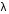 - длина волны; - длина волны;ω- циклическая частота колебаний, 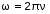 ; ;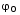 - начальная фаза колебаний. - начальная фаза колебаний.Скорость волны V, длина волны 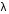 и частота колебаний и частота колебаний 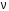 связаны соотношением связаны соотношением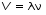 . (2) . (2)2.2. Рассмотрим пример образования стоячей упругой волны на струне. Предположим, что струна длиной L натянута вдоль оси OX, причем ее концы жестко закреплены (рис. 1). Возбудим на струне гармоническую волну с начальной фазой 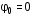 , бегущую вдоль оси OX слева направo , бегущую вдоль оси OX слева направo 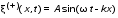 . .Если отражение волны от правого конца происходит без потери энергии, отраженная волна имеет такую же амплитуду, что и падающая, и описывается уравнением 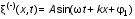 ,где ,где 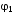 определяется изменением фазы при отражении. определяется изменением фазы при отражении. При сложении 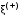 и и 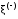 возникает интерференция и результирующая стоячая волна имеет вид возникает интерференция и результирующая стоячая волна имеет вид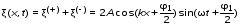 . .Величина 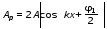 (3) (3)является амплитудой стоячей волны и зависит от координат точки. В случае, когда концы струны жестко закреплены, граничные условия имеют вид 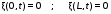 . (4) . (4)При отражении от закрепленного конца фаза волны меняется на 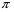 , ( , (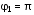 ). Тогда уравнение (3) примет вид ). Тогда уравнение (3) примет вид 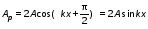 . (5) . (5)2.3. Покажем, что стоячая волна может существовать только при строго определенных частотах колебаний. Из второго граничного условия 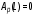 следует следует 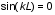 и и 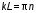 , где n - целое число. Следовательно, волновое число и длина волны могут иметь только следующие строго определенные значения: , где n - целое число. Следовательно, волновое число и длина волны могут иметь только следующие строго определенные значения: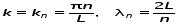 . .Таким образом, на струне возможны только те стоячие волны, половина длин которых укладывается на длине струны L целое число раз (рис. 1). 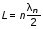 . (6) . (6)а  б  в  Рис. 1 Соответствующие этим длинам волн частоты колебаний 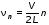 называются собственными частотами колебаний струны, а частота называются собственными частотами колебаний струны, а частота 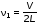 - основной частотой. Возбужденные в струне колебания с собственными частотами называются нормальными колебаниями струны (модами) или гармониками. Форма мод для n = 1, 2 и 3 показана на рис. 1. Первая мода называется основной. - основной частотой. Возбужденные в струне колебания с собственными частотами называются нормальными колебаниями струны (модами) или гармониками. Форма мод для n = 1, 2 и 3 показана на рис. 1. Первая мода называется основной.Точки, для которых амплитуда равна нулю, называются узлами стоячей волны. Точки, где амплитуда колебаний максимальна и равна 2A , называются пучностями. В пределах одной полуволны колебания всех точек происходят в фазе, при переходе к соседней полуволне фаза скачком меняется на π. 2.4. Отношение 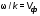 определяет фазовую скорость волны, для гармонических волн совпадающую по величине со скоростью распространения волн V. определяет фазовую скорость волны, для гармонических волн совпадающую по величине со скоростью распространения волн V. 2.5.Можно показать (см. приложение), что скорость распространения волны по струне зависит от силы натяжения струны T и ее погонной плотности ρ0 (массы на единицу длины) следующим образом: 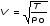 . (7) . (7)2.6. При воздействии на струну внешней гармонической силы на ней установится определенная мода колебаний, если ее частота совпадет с частотой вынуждающей силы. 2.7. В настоящей лабораторной работе изучаются закономерности нормальных колебаний струны, а именно: рассчитывается погонная плотность струны, сравниваются экспериментально найденные и теоретически рассчитанные скорости распространения волны при различных силах натяжения струны. 3. Описание лабораторной установки 3.1. Струна (медная проволока) закреплена одним концом на неподвижной стойке, к другому концу прикреплена чашечка. Переменный ток в струне создается генератором 3Г. Небольшой участок струны находится в поле электромагнита, питаемого от выпрямителя ВУ (рис. 2). Для измерения длины струны имеется масштабная линейка. 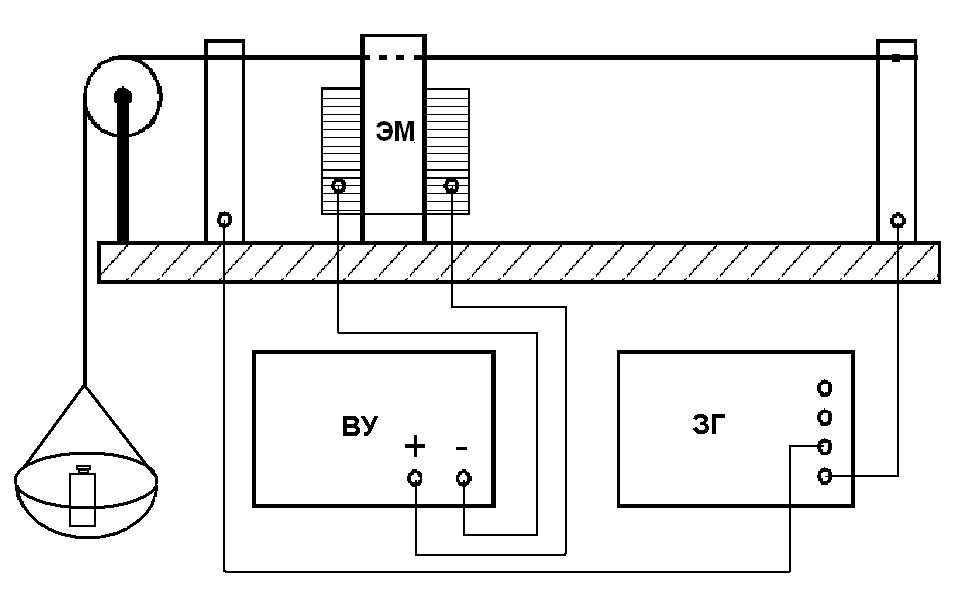 Рис. 2 3.2. В настоящей работе внешней вынуждающей силой является сила Ампера, с которой магнитное поле взаимодействует с участком струны, по которой протекает переменный ток. 3.3. Техника безопасности Корпуса генератора и выпрямителя должны быть заземлены. Запрещается включать приборы без разрешения преподавателя или лаборанта. 4. Порядок измерений 4.1. Внести технические данные приборов в табл. 1. Таблица 1
4.2. Измерить по линейке рабочую длину L струны. Внести величину в табл. 2. Туда же записать массу чашечки m0 (указана на её дне), ∆L и ∆m0 - приборные погрешности измерений, указанных выше величин. Таблица 2
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

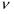 =
=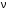 ,Гц
,Гц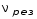 =
=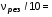
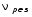 ,Гц
,Гц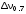 ,Гц
,Гц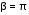
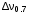 ,1/c
,1/c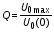
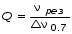
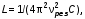 Гн
Гн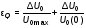
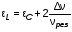
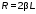 ,Ом
,Ом