ЕН.Ф.4 Эконометрика. Лекции 17 (час.) практические занятия 17 час семинарские занятия час лабораторные работы час
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
|
Тема 5. Оценка значимости уравнения и коэффициентов регрессии Учебные вопросы: Оценка значимости коэффициентов парной и множественной регрессионной модели. Оценка значимости уравнения парной и множественной регрессии. Принятие решения на основе уравнения регрессии. Определение доверительных интервалов для коэффициентов и функции регрессии. Проверить значимость уравнения регрессии значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной. F-тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы 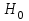 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического 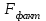 и критического (табличного) и критического (табличного) 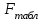 значений F-критерия Фишера. значений F-критерия Фишера. 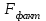 определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы: определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы: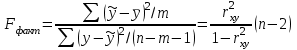 , ,где n – число единиц совокупности, m – число параметров при переменных x. 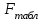 - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости 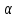 . Уровень значимости . Уровень значимости 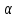 - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно 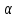 принимается равной 0.05 или 0.01. принимается равной 0.05 или 0.01.Если 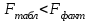 , то гипотеза , то гипотеза 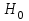 - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если же - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если же 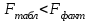 , то гипотеза , то гипотеза 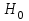 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии. не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы для каждого показателей. Выдвигается гипотеза 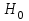 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки: о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки: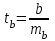 , , 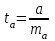 , , 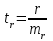 . .Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам: 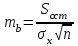 , , 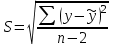 , ,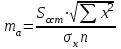 , (свободный коэффициент) , (свободный коэффициент)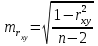 . .Сравнивая фактическое и критическое (табличное) значения t-статистики - 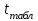 (при n-2 степенях свободы) и (при n-2 степенях свободы) и 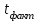 - принимаем или отвергаем гипотезу - принимаем или отвергаем гипотезу 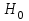 . .Если 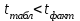 , то , то 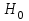 отклоняется, т.е. a, b, отклоняется, т.е. a, b, 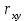 не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора x. Если не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора x. Если 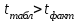 , то гипотеза , то гипотеза 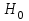 не отклоняется и признается случайная природа формирования a, b, не отклоняется и признается случайная природа формирования a, b, 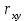 . .Для расчета доверительного интервала определяем предельную ошибку 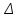 для каждого показателя: для каждого показателя: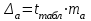 , , 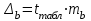 . .Формулы для расчета доверительных интервалов имеют следующий вид: 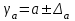 , , 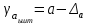 , , 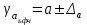 , ,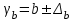 , , 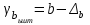 , , 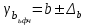 . .Прогнозное значение 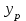 определяется путем подстановки в уравнение регрессии определяется путем подстановки в уравнение регрессии 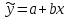 соответствующего (прогнозного) значения соответствующего (прогнозного) значения 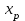 . . Экстраполяция кривой регрессии, т.е. ее использование вне пределов обследованного диапазона значений объясняющей переменной может привести к значительным погрешностям, поэтому при определении прогнозного значения строят и доверительные интервалы прогноза: Вычисляется средняя ошибка прогноза 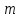 : :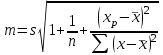 , ,где 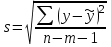 ; и строится доверительный интервал прогноза ; и строится доверительный интервал прогноза 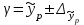 , где , где 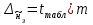 . .Величина стандартной ошибки достигает минимума при 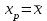 и возрастает по мере удаления от среднего значения в обе стороны. Результаты прогноза ухудшаются в зависимости от того, насколько прогнозное значение отклоняется от области наблюдений значений фактора x. и возрастает по мере удаления от среднего значения в обе стороны. Результаты прогноза ухудшаются в зависимости от того, насколько прогнозное значение отклоняется от области наблюдений значений фактора x.На графике доверительные границы для прогноза представляют собой гиперболы, расположенные по обе стороны от линии регрессии. В случае же множественной регрессии ее значимость оценивается с помощью F-критерия Фишера: 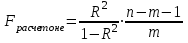 . .Если расчетное значение больше табличного при уровне значимости 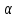 и m и n-m-1 степенях свободы, то уравнение считается статистически значимым, иначе – незначимым. и m и n-m-1 степенях свободы, то уравнение считается статистически значимым, иначе – незначимым.Оценка значимости коэффициентов регрессии осуществляется с помощью t-критерия Стьюдента и сводится к вычислению значений 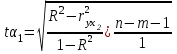 , ,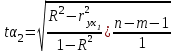 . .Если эти расчетные значения больше табличного при уровне значимости 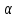 и n-m-1=n-3 (для двух факторных признаков) степенях свободы, то коэффициенты регрессии считаются статистически значимыми. и n-m-1=n-3 (для двух факторных признаков) степенях свободы, то коэффициенты регрессии считаются статистически значимыми.Вопросы для самопроверки: Опишите t-критерий Стьюдента. Опишите F – критерий Фишера. Как принимают решения на основе уравнения регрессии. Определение доверительных интервалов для коэффициентов и функции регрессии. Тема 6. Регрессионные модели с переменной структурой (фиктивные переменные) Учебные вопросы: Фиктивные переменные. Бинарные фиктивные переменные. Уравнение регрессии с фиктивной переменной. Интерпретация коэффициентов. Множественные совокупности фиктивных переменных. Фиктивные переменные для коэффициента наклона. Тест Чоу. Независимые переменные в регрессионных моделях, рассмотренные нами ранее, имеют непрерывные области изменения (национальный доход, уровень безработицы, размер заработной платы, стоимость товара и т.п.). Однако некоторые переменные могут принимать всего два значения или, в общей ситуации, дискретное множество значений. Необходимость рассматривать такие переменные возникает довольно часто в тех случаях, когда требуется принимать во внимание какой-либо качественный признак. Фиктивной называется переменная, которая является качественной по своей природе и, следовательно, не изменяется в числовой шкале. Примеры использования фиктивных переменных: Исследуется зависимость между доходом и потреблением в Приморском крае и выборка включает русские и корейские семьи. Ставится задача: имеет ли существенное значение это этническое происхождение. Исследуются факторы, определяющие инфляцию, и в некоторые годы правительство проводило политику регулирования доходов. Нужно проверить, оказало ли это влияние на зависимость. При исследовании зависимости заработной платы от различных факторов может возникнуть вопрос, влияет ли на ее размер, и если да, то в какой степени, наличие у работника высшего образования. Также можно поставить вопрос, существует ли дискриминация в оплате труда между мужчинами и женщинами. Исследуется зависимость между военными расходами и уровнем ВВП в разрезе стран мира (см. приложение). В выборку включены крупные и малочисленные страны. Требуется определить, будет ли одинаковой изучаемая зависимость для двух групп стран. Преимущества использования фиктивных переменных: возможность моделирования сезонных явлений; введение в исследование фиктивных переменных для коэффициента наклона. простой способ проверки, является ли воздействие качественного фактора значимым; Эконометрическая модель с фиктивной переменной имеет вид: 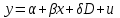 , ,г 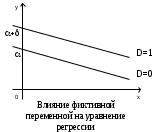 де D – фиктивная переменная, т.е. искусственно введенная переменная, принимающая значения 0 или 1. Ситуация определяется тем, что происходит при переменной D, равной 0 или 1. Если D = 0, то уравнение 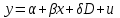 упрощается до вида упрощается до вида 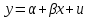 . .Использование сезонных фиктивных переменных При анализе временных рядов многие исследователи предпочитают квартальные данные годовым, поскольку их будет в 4 раза больше за рассматриваемый период. Вместе с тем иногда заметное воздействие на зависимость оказывает именно сезонность. Если не учесть ее, то она вносит свой вклад в случайную компоненту u. Рассмотрим зависимость 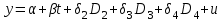 , ,где y – расходы электроэнергии по кварталам. Переменные 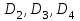 - фиктивные переменные, определяемые следующим образом: - фиктивные переменные, определяемые следующим образом: D2=1, если наблюдение относится ко 2 кварталу, и нулю в остальных случаях. D3=1, если наблюдение относится к 3 кварталу, и нулю в остальных случаях. D4=1, если наблюдение относится к 4 кварталу, и нулю в остальных случаях. Коэффициенты 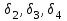 дают численную величину эффекта, вызываемого сменой сезонов. Коэффициент дают численную величину эффекта, вызываемого сменой сезонов. Коэффициент 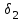 показывает дополнительную потребность электроэнергии во 2 квартале относительно 1 квартала, связанную со временем года. По аналогии показывает дополнительную потребность электроэнергии во 2 квартале относительно 1 квартала, связанную со временем года. По аналогии 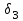 и и 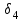 показывают соответствующие дополнительные количества электроэнергии в 3 и 4 кварталах относительно 1 квартала. Все эти сдвиги даются относительно 1 квартала, потому что он выбран в качестве эталонной категории. показывают соответствующие дополнительные количества электроэнергии в 3 и 4 кварталах относительно 1 квартала. Все эти сдвиги даются относительно 1 квартала, потому что он выбран в качестве эталонной категории.Таким образом, можем показать распределение значений фиктивных переменных в следующей таблице
Такое сезонное колебание можно изобразить графически на рисунке. 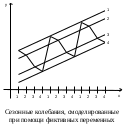 Из уравнения зависимости потребления электроэнергии можно получить модели для каждого квартала:
Усредняя четыре полученных уравнения, получим усредненную линию регрессии 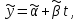 где где 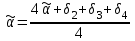 , а , а 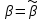 . Расстояние между определенной линией регрессии любого квартала и усредненной линией, которое представлено разностью значений постоянного члена в уравнении регрессий, дает оценку сезонных отклонений в рассматриваемом квартале. . Расстояние между определенной линией регрессии любого квартала и усредненной линией, которое представлено разностью значений постоянного члена в уравнении регрессий, дает оценку сезонных отклонений в рассматриваемом квартале. Она составляет для 1 квартала - 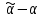 , для 2 квартала - , для 2 квартала - 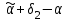 , для 3 квартала - , для 3 квартала - 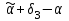 , для 4 квартала - , для 4 квартала - 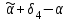 . Сумма сезонных отклонений должна быть равна 0, проверим это: . Сумма сезонных отклонений должна быть равна 0, проверим это: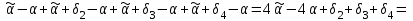 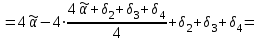 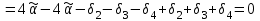 . .Выбор эталонной категории не оказывает воздействия на сущность уравнений регрессии. Сам выбор определяет форму представления коэффициента регрессии. Пусть в нашем примере выбрана эталонная категория для второго квартала. Тогда вводим новую фиктивную переменную 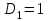 , если наблюдение относится к 1 кварталу, и 0 иначе и опустим переменную , если наблюдение относится к 1 кварталу, и 0 иначе и опустим переменную 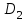 , т.к. фиктивная переменная для эталонной категории не включается в уравнение регрессии. Переменные , т.к. фиктивная переменная для эталонной категории не включается в уравнение регрессии. Переменные 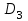 и и 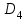 включаются в уравнение с теми же определениями, что и раньше. Получим включаются в уравнение с теми же определениями, что и раньше. Получим 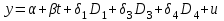 Положим 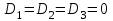 и получим вариант уравнения для 1 квартала: и получим вариант уравнения для 1 квартала: 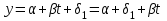 . .Но интерпретация коэффициентов регрессии при введении новой эталонной переменной будет уже иной. Так, например, для уравнения 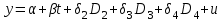 коэффициент коэффициент 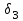 оценивает разность между потребленной электроэнергией в третьем и первом кварталах, а в уравнении оценивает разность между потребленной электроэнергией в третьем и первом кварталах, а в уравнении 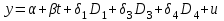 коэффициент коэффициент 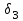 есть разность между потребленной электроэнергией в 3-ем и 2-ом кварталах. Если включить в уравнение фиктивную переменную для эталонной категории то: есть разность между потребленной электроэнергией в 3-ем и 2-ом кварталах. Если включить в уравнение фиктивную переменную для эталонной категории то: Если бы было возможно вычислить коэффициент регрессии, то им невозможно дать интерпретацию. Фактически станет невозможной процедура вычисление коэффициентов уравнений регрессии. Аналогично можно смоделировать сезонные колебания спроса на мороженое. Ранее предполагалось, что качественные переменные, введенные в уравнение регрессии, отвечают только за сдвиги в значении постоянного члена в уравнении регрессии, а наклон линии регрессии одинаков для каждой категории переменных. Рассмотрим теперь фиктивные переменные коэффициента наклона. Для этого введем в рассмотрение модель: 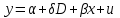 , ,где y – вес новорожденного (в граммах), x – количество выкуренных мамой в день сигарет, D - фиктивная переменная, принимающая значение D=1, если не первый ребенок и D = 0, если первый ребенок. В этой формулировке явно предположение о том, что воздействие курения на вес новорожденного одинаково, независимо от того, первый ребенок или нет. Добавим в уравнение член 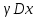 - произведение D и x с коэффициентом - произведение D и x с коэффициентом 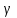 : : 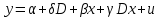 , ,перепишем в виде 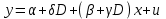 . .Если принять D=0, то 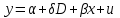 и угловой коэффициент и угловой коэффициент 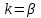 . Если же D=1, то . Если же D=1, то 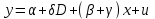 и угловой коэффициент и угловой коэффициент 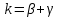 . Поэтому величина . Поэтому величина 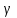 рассматривается как разность между коэффициентом при показателе интенсивности курения в случае не первого ребенка и коэффициентом при показателе интенсивности курения в случае первого ребенка. Показатель Dx – фиктивная переменная для коэффициента наклона. Он рассматривается как третья объясняющая переменная. Модель может иметь вид: рассматривается как разность между коэффициентом при показателе интенсивности курения в случае не первого ребенка и коэффициентом при показателе интенсивности курения в случае первого ребенка. Показатель Dx – фиктивная переменная для коэффициента наклона. Он рассматривается как третья объясняющая переменная. Модель может иметь вид: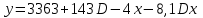 . .Результат оценивания регрессии показывает, что снижение веса новорожденного, связанное с курением матери, значительно больше, для первого ребенка – 12,1 г на каждую сигарету в день против 4 г для непервого. Регрессионная зависимость веса новорожденного (y) от интенсивности курения (x – число выкуренных в день сигарет), фиктивной переменной D (D=0 – первый ребенок, D=1 – не первый), фиктивной переменной М пола ребенка (М=0 – для девочек, М=1 для мальчиков), и фиктивной переменной для коэффициента наклона Mх, определяемой как произведение M на х, имеет вид 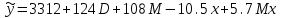 . .Возможны 4 случая различных попарных значений фиктивных переменных D и M: 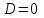 , , 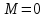 , , 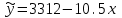 . .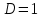 , , 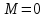 , , 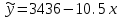 . .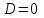 , , 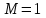 , , 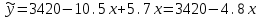 . .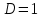 , , 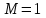 , , 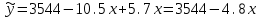 . .Результат регрессии показывает, что снижение веса новорожденного, связанного с курением матери, значительно больше, если должна родиться девочка – 10,5 г против 4,8 г для мальчиков. Вопрос в аудиторию. Какую модель необходимо построить, чтобы ответить на вопрос: каково снижение веса, связанное с показателем курения, на первого мальчика или непервую девочку? Какую фиктивную переменную для коэффициента наклона необходимо ввести? Тест Чоу На практике нередки случаи, когда имеются две выборки пар значений зависимой и объясняющих переменных. Например, одна выборка пар значений переменных объемом n1 получена при одних условиях, а другая объемом n2 - при других несколько измененных условиях. Необходимо выяснить, действительно ли две выборки однородны в регрессионном смысле? Другими словами, можно ли объединить эти две подвыборки в одну и рассматривать единую модель регрессии? Ответ на этот вопрос может дать тест Чоу. Иногда выборка наблюдений состоит: из двух или более подвыборок, и трудно установить, следует ли оценивать одну объединяющую регрессию или отдельные регрессии для каждой подвыборки. Пусть имеется 2 выборки А и В. Обозначим суммы квадратов остатков для регрессий подвыборок А и В через: 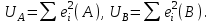 Пусть суммы квадратов остатков в объединенной регрессии для наблюдений, относящихся к двум подвыборкам, равны соответственно 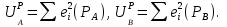 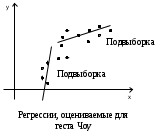 Т.к. отдельные регрессии для подвыборок должны соответствовать наблюдениям так же хорошо, если не лучше, чем объединенная регрессия, то 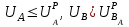 . . Складывая неравенства 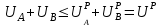 , где , где 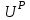 - общая сумма квадратов остатков, - общая сумма квадратов остатков, 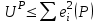 . .Предположим, что имеются данные временного ряда по двум переменным и что в период выборки произошли структурные изменения, разд4еляющие наблюдения на подвыборки А и В. И 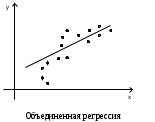 з рисунка видно, что если бы потребовалось объединить регрессию, то остатки были бы значительно больше. В регрессии имеется k объясняющих переменных плюс одна константа, следовательно, имеем k + 1 степень свободы. Рассмотрим F- статистику 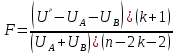 с (k+1) и (n-2k-2) степенями свободы. Если 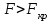 , то не следует оценивать объединенную регрессию, а если , то не следует оценивать объединенную регрессию, а если 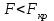 , то следует ее оценить. , то следует ее оценить. 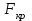 определяется из таблицы F- распределения Фишера при уровне значимости определяется из таблицы F- распределения Фишера при уровне значимости 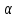 и с (k+1) и (n-2k-2) степенями свободы. и с (k+1) и (n-2k-2) степенями свободы. Вопросы для самопроверки: Опишите механизм применения фиктивных переменных в эконометрическом моделировании. Использование сезонных фиктивных переменных в модели потребления электроэнергии. Опишите пример использования множественных фиктивных переменных. Модельные примеры: влияет ли пол на уровень успеваемости студентов, одинакова ли в крупных и мелких странах зависимость военных расходов от ВВП. Используйте тест Чоу. |