ЕН.Ф.4 Эконометрика. Лекции 17 (час.) практические занятия 17 час семинарские занятия час лабораторные работы час
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
КОНСПЕКТЫ ЛЕКЦИЙпо дисциплине«Эконометрика»Специальность 080105.65 «Финансы и кредит» г. Спасск-Дальний 2012 1. Структура и содержание теоретической части курса (17 часов) Тема 1. Введение в эконометрику Учебные вопросы: Предмет, метод и задачи эконометрики. Связь эконометрики с экономической теорией, математической и экономической статистикой. Эконометрический метод. Эконометрическая модель. Типы моделей. Типы данных. Основные этапы эконометрического моделирования. Компьютеры и эконометрическая практика. В экономической теории обычно выделяют макроэкономику, микроэкономику и эконометрику. Термин «эконометрика» состоит из двух частей: «эконо» от «экономика» и «метрика» - от «измерение», т.е. дословно это означает «наука об экономических измерениях». Эконометрика входит в обширное семейство дисциплин, посвященных измерениям в различных областях науки. Так, существует биометрика, психометрика, хемометрика, технометрика и другие. Эконометрика, как и другие «метрики», посвящена развитию и применению статистических методов в конкретной области науки и практики – в экономике. Итак, эконометрикой называется статистический анализ экономических данных. Впервые этот термин был введен в 1926 г. норвежским ученым Рагнаром Фришем. Сам термин эконометрика введен в научный оборот в 1926 норвежским экономистом Р. Фришем (1895-1973), хотя впервые был сконструирован в 1910 польским экономистом П. Чомпа. Р. Фриш совместно с американцами И. Фишером, Ч. Рузом и другими основал Международное эконометрическое общество (1930). Эконометрика – раздел экономики, занимающийся разработкой и применением статистических методов для измерений взаимосвязей между экономическими переменными. Предметом эконометрики являются факторы, формирующие развитие экономических явлений и процессов. С помощью эконометрических методов можно, например, Исследовать выпуск промышленной продукции в зависимости от различных социально-экономических параметров. Проанализировать рынок подержанных автомобилей в России. Проводить долгосрочное и краткосрочное прогнозирование инфляции и номинального валютного курса в РФ. Проводить маркетинговые исследования (анализ зависимости спроса и знания марки от объема рекламы). Объективную характеристику развития экономических явлений и процессов в будущем (т.е. в прогнозировании) могут обеспечить правильно подобранные эконометрические методы. К основным методам эконометрики относятся: метод наименьших квадратов; обобщенный МНК; косвенный метод наименьших квадратов; двухшаговый и трехшаговый МНК; оценивание систем одновременных уравнений; метод максимального правдоподобия. В эконометрике выделяют три вида научной и прикладной деятельности: разработка методов прикладной статистики с учетом специфики экономических данных; разработка эконометрических моделей в соответствии с конкретными потребностями экономической науки и практики; применение эконометрических методов для статистического анализа конкретных экономических данных. Во всей этой деятельности существенным является использование моделей. Можно выделить три основных класса моделей, которые применяются для анализа и/или прогноза: модели временных рядов трендовые модели 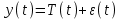 ; ;сезонные модели 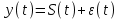 ; ;модели тренда и сезонности 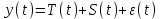 ; ;где 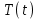 - временной тренд заданного параметрического вида, - временной тренд заданного параметрического вида, 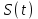 - периодическая (сезонная) компонента, - периодическая (сезонная) компонента, 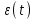 - случайная компонента. - случайная компонента.К моделям временных рядов относится и множество более сложных моделей, таких как, модели адаптивного прогноза, модели авторегрессии, скользящего среднего и др. Такие модели могут применяться при изучении и прогнозировании объема продаж автомобилей, спроса на мороженое, краткосрочного прогноза процентных ставок и др. регрессионные модели с одним уравнением: 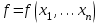 . В зависимости от вида функции f модели делятся на линейные и нелинейные. Например, можно исследовать спрос на мороженое как функцию от времени, температуры воздуха, среднего уровня доходов или зависимость заработной платы от возраста, пола, стажа, образования и т.п. Область применения таких моделей намного шире, чем временных рядов. Эта тема является основной в эконометрике. . В зависимости от вида функции f модели делятся на линейные и нелинейные. Например, можно исследовать спрос на мороженое как функцию от времени, температуры воздуха, среднего уровня доходов или зависимость заработной платы от возраста, пола, стажа, образования и т.п. Область применения таких моделей намного шире, чем временных рядов. Эта тема является основной в эконометрике. системы одновременных уравнений. Особенностью этих систем является то, что каждое из уравнений системы может включать объясняемые переменные из других уравнений. Имеет место набор зависимых переменных. В системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и независимые в других. Классическим примером системы одновременных уравнений является модель спроса и предложения, где спрос на товар определяется его ценой P и доходом I, а предложение – его ценой P и достигается равновесие между спросом и предложением: 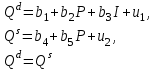 В этой системе экзогенной (задаваемой извне) переменной выступает доход I, а эндогенными – спрос (предложение) товара 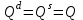 и цена товара (цена равновесия) P. и цена товара (цена равновесия) P. Для получения достоверных и информативных данных о распределении какой-либо случайной величины, необходимо иметь выборку ее наблюдений достаточно большого объема. Выборка – набор значений 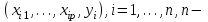 число наблюдений. При моделировании экономических процессов встречаются с двумя типами данных: число наблюдений. При моделировании экономических процессов встречаются с двумя типами данных:пространственные данные (пространственная выборка) – набор показателей экономических переменных, полученный в данный момент времени. Примером может быть набор данных - объем продаж, количество работников, доход и др. по разным фирмам в один и тот же момент времени. Другой пример – курсы покупки-продажи валюты в один день по обменным пунктам города; временные данные – выборка наблюдений, в которой важны не только сами значения случайных величин, но и порядок их следования друг за другом. Пример: ежеквартальные данные по инфляции, средней заработной плате, национальному доходу и т.д. К задачам эконометрики относятся предоставление количественных зависимостей для экономических соотношений; систематическое и эффективное обеспечение процесса принятия управленческих решений; прогнозирование социально-экономических явлений; формирование рекомендаций по экономической политике. Пусть, например, ставится задача определить цену – величину, формируемую под воздействием некоторых факторов (тип дома, наличие балкона, площадь кухни и т.д.) Такие зависимые переменные называются зависимыми или результативными, а факторы, от которых они зависят – объясняющими или факторными. Указанная конкретная цена – наблюдаемое значение зависимой переменной зависит также и от случайных переменных, например, характера продавца, его потребность в конкретной денежной сумме и т.д. Таким образом, зависимая переменная разбивается на две части – объясненную и случайную. В общем виде эконометрическая модель имеет вид: y=f(x)+u, где y – наблюдаемое значение зависимой переменной, f(x) - объясненная часть, зависящая от значений факторных признаков, u - случайная составляющая. Пусть получено выражение для объясненной части переменной y: 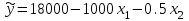 , где , где 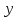 - ожидаемая цена автомобиля, - ожидаемая цена автомобиля, 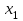 - срок эксплуатации в годах, - срок эксплуатации в годах, 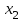 - пробег в тыс. км. Каково практическое применение полученного результата? - пробег в тыс. км. Каково практическое применение полученного результата?Результат позволяет понять, как именно формируется рассматриваемая экономическая переменная – цена на автомобиль, Он дает возможность выявить влияние каждой из объясняющих переменных на цену автомобиля, Результат позволяет прогнозировать цену на автомобиль, если известны его основные параметры. Основные этапы эконометрического моделирования 1-ый этап (постановочный). Формируется цель исследования, набор участвующих в модели экономических переменных. В качестве цели эконометрического моделирования обычно рассматривают анализ исследуемого экономического объекта (процесса); прогноз его экономических показателей, имитацию развития объекта при различных значениях экзогенных переменных (отражая их случайный характер, изменение во времени), выработку управленческих решений. При выборе экономических переменных необходимо теоретическое обоснование каждой переменной (при этом рекомендуется, чтобы число их было не очень большим и, как минимум, в несколько раз меньше числа наблюдений). Объясняющие переменные не должны быть связаны функциональной или тесной корреляционной зависимостью, так как это может привести к невозможности оценки параметров модели или к получению неустойчивых, не имеющим реального смысла оценок, т. е. к явлению мультиколлинеарности. Для отбора переменных могут быть использованы различные методы, в частности процедуры пошагового отбора переменных.. А для оценки влияния качественных признаков (например, пол, образование и т. п.) могут быть использованы фиктивные переменные. Но в любом случае определяющим при включении в модель тех или иных переменных является экономический (качественный) анализ исследуемого объекта. 2-й этап (априорный). Проводится анализ сущности изучаемого объекта, формирование и формализация априорной (известной до начала моделирования) информации. 3-й этап (параметризация). Осуществляется непосредственно моделирование, т.е. выбор общего вида модели, выявление входящих в нее связей. Основная задача, решаемая на этом этапе, — выбор вида функции f(x) в эконометрической модели, в частности, возможность использования линейной модели как наиболее простой и надежной. Весьма важной проблемой на этом (и предыдущих) этапе эконометрического моделирования является проблема спецификации модели, в частности: выражение в математической форме обнаруженных связей и соотношений; установление состава экзогенных и эндогенных переменных; формулировка исходных предпосылок и ограничений модели. От того, насколько удачно решена проблема спецификации модели, в значительной степени зависит успех всего эконометрического моделирования. 4-й этап (информационный). Осуществляется сбор необходимой статистической информации — наблюдаемых значений экономических переменных. Здесь могут быть наблюдения, полученные как с участием исследователя, так и без его участия (в условиях активного или пассивного эксперимента). 5-й этап (идентификация модели). Осуществляется статистический анализ модели и оценка ее параметров. 6-й этап (верификация модели). Проводится проверка истинности, адекватности модели. Выясняется, насколько удачно решены проблемы спецификации, идентификации модели, какова точность расчетов по данной модели, в конечном счете, насколько соответствует построенная модель моделируемому реальному экономическому объекту или процессу. Если имеются статистические данные, характеризующие моделируемый экономический объект в данный и предшествующие моменты времени, то для верификации модели, построенной для прогноза, достаточно сравнить реальные значения переменных в последующие моменты времени с соответствующими их значениями, полученными на основе рассматриваемой модели по данным предшествующих моментов. Приведенное выше разделение эконометрического моделирования на отдельные этапы носит в известной степени условный характер, так как эти этапы могут пересекаться, взаимно дополнять друг друга и т. п. Вопросы для самопроверки: Сформулируйте предмет эконометрики. Опишите связь эконометрики с экономической теорией, математической и экономической статистикой. Эконометрический метод. Эконометрическая модель. Типы моделей. Какие типы данных используются в эконометрике? Перечислите основные этапы эконометрического моделирования. Какие компьютерные программы для эконометрических расчетов Вам известны? Тема 2. Парная линейная и нелинейная регрессия и корреляция Учебные вопросы: Модель парной линейной регрессии. Экономическая интерпретация. Метод наименьших квадратов. Линейный коэффициент корреляции как показатель тесноты связи между явлениями. Свойства линейного коэффициента корреляции. Шкала Чеддока. Графическая интерпретация линейного коэффициента корреляции. Коэффициент детерминации. Показатели качества регрессии. Нелинейная парная регрессия на основе метода наименьших квадратов. Индекс корреляции нелинейной регрессии. Индекс детерминации. Парная регрессия – уравнение связи двух переменных y и х: 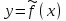 , где y – зависимая переменная (результативный признак), x – независимая, объясняющая переменная (факторный признак). Различают линейные и нелинейные регрессии. Пусть имеются некоторые статистические данные двух признаков. Поставим задачу получить количественное выражение гипотетического линейного соотношения между двумя переменными. , где y – зависимая переменная (результативный признак), x – независимая, объясняющая переменная (факторный признак). Различают линейные и нелинейные регрессии. Пусть имеются некоторые статистические данные двух признаков. Поставим задачу получить количественное выражение гипотетического линейного соотношения между двумя переменными. В  случае парной линейной регрессии рассмотрим простейшую модель 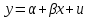 . Величина y, рассматриваемая как зависимая переменная, состоит из двух составляющих: 1) неслучайная составляющая . Величина y, рассматриваемая как зависимая переменная, состоит из двух составляющих: 1) неслучайная составляющая 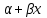 , где x – объясняющая или независимая переменная, , где x – объясняющая или независимая переменная, 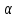 и и 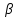 – параметры уравнения; 2) случайного члена u. – параметры уравнения; 2) случайного члена u. 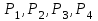 - реальные значения, - реальные значения, 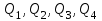 - точки зависимости если бы не было случайного члена. - точки зависимости если бы не было случайного члена.Чем меньше u, тем легче задача. Если бы не было случайного члена, то точки P совпали с Q и точно показали бы положение прямой. К причинам возникновения случайного члена можно отнести следующие: Невключение объясняющих переменных. Т.е. существуют другие факторы, влияющие на у, которые не учтены в уравнении. Влияние их приводит к тому, что точки не лежат на одной прямой. Агрегирование переменных. Рассматриваемая зависимость является попыткой объединить некоторое число объектов, которые возможно обладают различными характеристиками. Функция суммарного потребления - попытка выражения совокупных решений отдельных индивидуумов о расходах, следовательно, возникает аппроксимация, следовательно, расхождение приписывается случайному члену. Неправильное описание структуры модели. Т.е., например, если зависимость относится к данным о временном ряде, то значение у может зависеть не от фактического значения x, а от значения, которое ожидалось в предыдущем периоде. Если ожидаемое и фактическое значение тесно связанны, то будет казаться, что между y и x существует зависимость, но это будет лишь аппроксимация, и расхождение вновь будет связанно с наличием случайного члена. Неправильная функциональная спецификация. Т.е. функциональное соотношение между y и x может быть определено неправильно. Например, зависимость может не являться линейной, а быть более сложной – нелинейной. Ошибки измерения. Если в измерении одной или более взаимосвязанных переменных имеются ошибки, то наблюдаемые значения не будут соответствовать такому соотношению, и существующие расхождения будут вносить вклад в остаточный член. |
