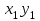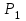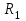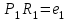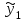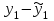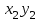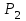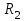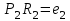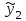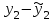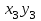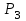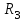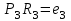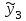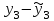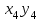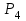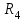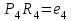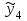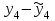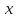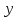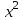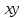ЕН.Ф.4 Эконометрика. Лекции 17 (час.) практические занятия 17 час семинарские занятия час лабораторные работы час
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
Регрессия по методу наименьших квадратовРассмотрим уравнение 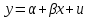 . Имеется информация о четырех наблюдениях для x и y. Требуется определить . Имеется информация о четырех наблюдениях для x и y. Требуется определить 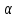 и и 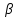 . В качестве грубой аппроксимации можно построить прямую, в наибольшей степени соответствующей этим точкам. Отрезок, отсекаемый на оси ординат а – оценка . В качестве грубой аппроксимации можно построить прямую, в наибольшей степени соответствующей этим точкам. Отрезок, отсекаемый на оси ординат а – оценка 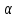 , угловой коэффициент прямой b – оценка , угловой коэффициент прямой b – оценка  . . 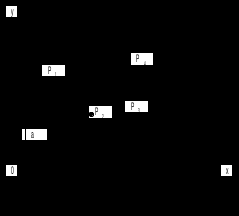 Возникает вопрос: существует ли способ достижения точной оценки  и и  алгебраическим путем? Определим остатки для каждого наблюдения: алгебраическим путем? Определим остатки для каждого наблюдения:
И  так, остатки равны 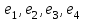 . Очевидно, что мы хотим построим линию регрессии так, чтобы эти остатки были минимальными. . Очевидно, что мы хотим построим линию регрессии так, чтобы эти остатки были минимальными. Но необходимо выбрать такой критерий подбора, который будет одновременно учитывать величину всех остатков. Одним из способов поставленной задачи состоит в минимизации суммы квадратов остатков: 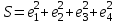 , ,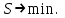 Если S=0, то все остатки равны нулю. В этом случае линия регрессии проходит через все точки. Однако, это невозможно из-за наличия случайного члена. Существуют и другие достаточно различные решения, однако при выполнении определенных условий метод наименьших квадратов дает несмещенные и эффективные оценки для 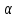 и и 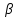 . Рассмотрим обычный метод наименьших квадратов, далее будут рассмотрены другие его варианты, которые могут быть использованы для решения некоторых специальных проблем. . Рассмотрим обычный метод наименьших квадратов, далее будут рассмотрены другие его варианты, которые могут быть использованы для решения некоторых специальных проблем.Рассмотрим случай, когда имеется n наблюдений двух переменных x и y. Предположив, что y зависит от x, будем искать уравнение вида 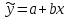 . Для наблюдения i расчетное значение зависимой переменной равно . Для наблюдения i расчетное значение зависимой переменной равно 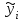 , а , а 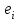 - остаток. Сумма квадратов остатков будет равна: - остаток. Сумма квадратов остатков будет равна: 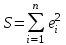 . Распишем квадрат i-го остатка: . Распишем квадрат i-го остатка: 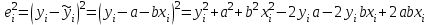 . .Суммируя по всем n наблюдениям, запишем S в виде: 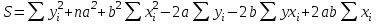 . .Составляем систему нормальных уравнений для коэффициентов регрессии 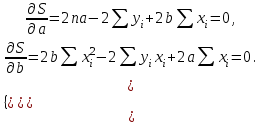 Выразим из систему двух уравнений с двумя неизвестными параметры a и b. Из первого уравнения 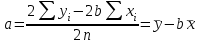 . .Подставив выражение для a во второе уравнение системы и выразив b, получим ряд следующих преобразований 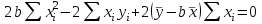 , ,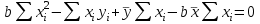 , ,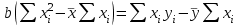 , ,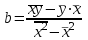 . .Полученные оценки для коэффициентов уравнения регрессии можно проинтерпретировать в два этапа: Словесное истолкование уравнения. Решение вопроса о том, следует ли ограничиться этим или провести более детальное исследование зависимости. Пусть получено следующее уравнение регрессии 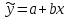 , где x и y – переменные с простыми естественными единицами измерения. Тогда: , где x и y – переменные с простыми естественными единицами измерения. Тогда:Увеличение x на 1 единицу (в единицах измерения x) приведет к увеличению значения y на b единиц (в единицах измерения y). Следует заменить слово «единица» фактическим количеством. Проверка возможности более простого выражения результата, который может оказаться наиболее удобным. Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции для линейной регрессии: 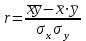 . .Свойства коэффициента корреляции: Абсолютная величина коэффициента корреляции не превосходит единицы: 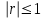 . .Если соответствующие значения переменных x и y представлены в корреляционной таблице, то условие 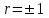 является необходимым и достаточным, чтобы y и x были связаны линейной функциональной зависимостью. является необходимым и достаточным, чтобы y и x были связаны линейной функциональной зависимостью.Если регрессия является точно линейной и 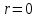 , то между y и х нет линейной корреляционной зависимости. , то между y и х нет линейной корреляционной зависимости.Рассмотрим пример. Пример 2.1. Пусть требуется найти зависимость между y и х по следующим данным:
а). Будем искать зависимость в виде 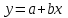 . Остатки в наблюдениях соответственно равны: . Остатки в наблюдениях соответственно равны: 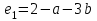 , , 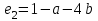 , , 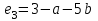 . Составим сумму квадратов этих остатков . Составим сумму квадратов этих остатков 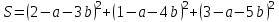 . Возводя в квадрат и приводя подобные слагаемые получим функцию от двух переменных a и b: . Возводя в квадрат и приводя подобные слагаемые получим функцию от двух переменных a и b: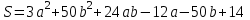 . .Вычисляем частные производные, приравниваем их нулю, решаем систему нормальных уравнений: 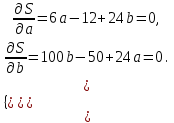 Решением этой системы является пара 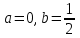 . Таким образом уравнение регрессии имеет вид . Таким образом уравнение регрессии имеет вид 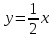 . .b). На практике нет смысла ограничиваться тремя наблюдениями, поэтому решение, предложение в пункте a) затруднительно. Воспользуемся на модельном примере формулами, выведенными выше 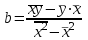 , ,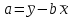 . .Составим расчетную таблицу, в последней строке которой приведены суммы соответствующих столбцов.
Вычислим средние: 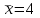 , , 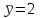 , , 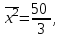 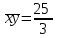 . Тогда получим оценки: . Тогда получим оценки: 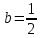 , , 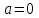 , что совпадает с оценками, полученными в пункте а). Вычисляя дисперсии , что совпадает с оценками, полученными в пункте а). Вычисляя дисперсии 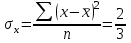 , , 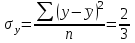 можно найти оценку тесноты связи – коэффициент корреляции можно найти оценку тесноты связи – коэффициент корреляции 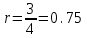 . .Нелинейная парная регрессия на основе метода наименьших квадратов Одним из недостатков линейного регрессионного анализа является то, что он может быть применен только к линейным уравнениям вида: 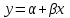 . .Например, уравнения вида 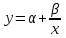 и и 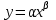 является нелинейным. Все нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам. является нелинейным. Все нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.Регрессии, нелинейные по объясняющим переменным: полиномы разных степеней 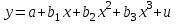 , ,равносторонняя гипербола 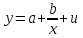 . .Регрессии, нелинейные по оцениваемым параметрам: степенная 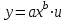 , ,показательная 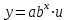 , ,экспоненциальная 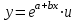 . .Р  ассмотрим подробнее зависимости 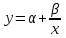 и и 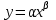 . Графически эти зависимости имеют вид, показанный на рисунке 2.4. . Графически эти зависимости имеют вид, показанный на рисунке 2.4.1. 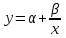 - это обратная зависимость между x и y. Это регрессия на основе гиперболы. Выведем оценки a и b параметров - это обратная зависимость между x и y. Это регрессия на основе гиперболы. Выведем оценки a и b параметров 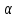 и и 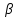 . Составляем функцию суммы квадратов остатков. . Составляем функцию суммы квадратов остатков. 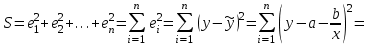 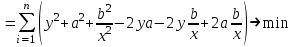 . .Для определения параметров a и b необходимо решить систему нормальных уравнений: 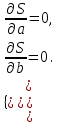 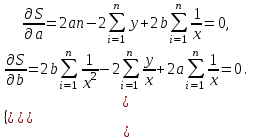 Деля уравнение на 2n, получим: 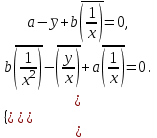 Решая систему двух уравнений с двумя неизвестными, получим 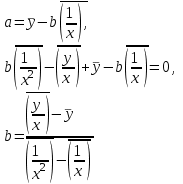 2. Рассмотрим теперь функцию 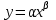 (это степенные функции). Обнаружим, что соотношение (это степенные функции). Обнаружим, что соотношение 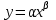 может быть преобразовано в линейное уравнение путем использования логарифмов. Прологарифмируем обе части этого тождества: может быть преобразовано в линейное уравнение путем использования логарифмов. Прологарифмируем обе части этого тождества: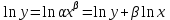 . .Заменим 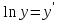 , , 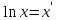 , , 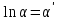 , тогда , тогда 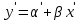 , т.е. получим линейную функцию. В этом случае процедура оценивания параметров состоит в следующем: , т.е. получим линейную функцию. В этом случае процедура оценивания параметров состоит в следующем:Вычислить 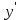 и и 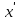 для каждого наблюдения путем взятия логарифмов от исходных данных. для каждого наблюдения путем взятия логарифмов от исходных данных. Оценить линейную зависимость 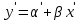 , в результате чего получим оценки , в результате чего получим оценки 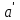 и b. Здесь b является непосредственной оценкой, а и b. Здесь b является непосредственной оценкой, а 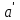 является оценкой является оценкой 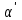 , т.е. , т.е. 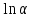 . . Переход к прежним переменным: 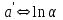 , , 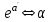 - оценка - оценка 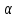 . .Таким образом, 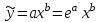 . . Частным случаем степенной функции 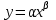 является квадратичная функция является квадратичная функция 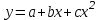 . Составляем сумму квадратов остатков: . Составляем сумму квадратов остатков: 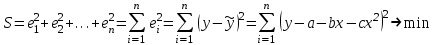 Для определения параметров a, b и с необходимо решить систему нормальных уравнений: 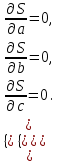 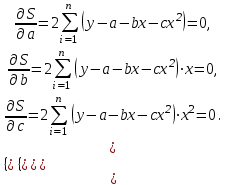 Деля уравнение на 2n получим систему трех уравнений с тремя неизвестными: 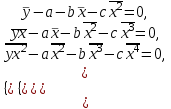 Подставляя расчетные средние 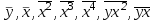 и решая систему уравнений, находим a, b, c. и решая систему уравнений, находим a, b, c.Тесноту связи изучаемых явлений оценивает индекс корреляции для нелинейной регрессии 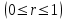 : : 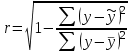 . .При анализе можно также рассчитывать среднюю ошибку аппроксимации – среднее отклонение расчетных значений от фактических: 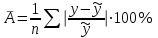 . .Допустимый предел значений 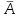 – не более 8-10%. – не более 8-10%. |