|
|
ЕН.Ф.4 Эконометрика. Лекции 17 (час.) практические занятия 17 час семинарские занятия час лабораторные работы час
по дисциплине «Эконометрика»
Специальность 080105.65 «Финансы и кредит»
г. Спасск-Дальний
2012
Перечень индивидуальных домашних заданий
ИДЗ 1. По статистическим данным приложения 3 по любым двум валютам проверьте тест на наличие автокорреляции Дарбина-Уотсона. Постройте уравнение зависимости с учетом автокорреляции.
ИДЗ 2. Зависимость реальной ставки процентов от темпа инфляции представлена уравнением регрессии: 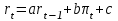 . Исходные данные можно взять на сайтах http://www.finam.ru/analysis/macroevent/default.asp, www.hse.ru, www.cbr.ru. Проведите анализ и сделайте вывод. . Исходные данные можно взять на сайтах http://www.finam.ru/analysis/macroevent/default.asp, www.hse.ru, www.cbr.ru. Проведите анализ и сделайте вывод.
ИДЗ 3. В одной из аграрных стран строилась функция потребления за 1988 – 1997 гг. по данным (в условных денежных единицах), представленных в таблице. Постройте функцию потребления, используя модель Кейнса формирования доходов. Дайте интерпретацию результатов приведенной формы модели.
Показатель
|
1988
|
1989
|
1990
|
1991
|
1992
|
1993
|
1994
|
1995
|
1996
|
1997
|
Совокупное потребление
|
1900
|
1980
|
2000
|
1800
|
2000
|
2100
|
2200
|
2100
|
2050
|
2100
|
Объем инвестиций
|
100
|
200
|
300
|
200
|
100
|
200
|
300
|
200
|
150
|
300
|
Совокупный доход
|
2000
|
2180
|
2300
|
2000
|
2100
|
2300
|
2500
|
2300
|
2200
|
2400
|
ИДЗ 4. По статистической выборке цен на автомобили (BMW) в салонах введите фиктивные переменные в исследование, опишите их. Вычислите матрицу парных коэффициентов корреляций, проанализируйте ее. На основе этого анализа выделите два наиболее существенных фактора, от которых зависит цена машины. Напишите уравнение множественной регрессии, проинтерпретируйте коэффициенты. Вычислите коэффициент множественной корреляции и детерминации. Оцените значимость полученного уравнения и коэффициентов регрессии. Сделайте вывод о возможности прогнозирования по данной модели. Проделайте расчеты в ППП MS Excel.
ИДЗ 5. Оцените модель экспорта, предложенную голландским экономистом Я.Тинбергеном. Страны: российский Дальний Восток, Япония, Корея, Китай.
Статистико-математические таблицы
Таблица значений F-критерия Фишера при уровне значимости  . .
k2\k1
|
1
|
2
|
3
|
4
|
5
|
6
|
8
|
12
|
24
|
|
1
|
161.45
|
199.50
|
215.72
|
224.57
|
230.17
|
233.97
|
238.89
|
243.91
|
249.04
|
254.32
|
2
|
18.51
|
19.00
|
19.16
|
19.25
|
19.30
|
19.33
|
19.37
|
19.41
|
19.45
|
19.50
|
3
|
10.13
|
9.55
|
9.28
|
9.12
|
9.01
|
8.94
|
8.84
|
8.74
|
8.64
|
8.53
|
4
|
7.71
|
6.94
|
6.59
|
6.39
|
6.26
|
6.16
|
6.04
|
5.91
|
5.77
|
5.63
|
5
|
6.61
|
5.79
|
5.41
|
5.19
|
5.05
|
4.95
|
4.82
|
4.68
|
4.53
|
4.36
|
6
|
5.99
|
5.14
|
4.76
|
4.53
|
4.39
|
4.28
|
4.15
|
4.00
|
3.84
|
3.67
|
7
|
5.59
|
4.74
|
4.35
|
4.12
|
3.97
|
3.87
|
3.73
|
3.57
|
3.41
|
3.23
|
8
|
5.32
|
4.46
|
4.07
|
3.84
|
3.69
|
3.58
|
3.44
|
3.28
|
3.12
|
2.93
|
9
|
5.12
|
4.26
|
3.86
|
3.63
|
3.48
|
3.37
|
3.23
|
3.07
|
2.90
|
2.71
|
10
|
4.96
|
4.10
|
3.71
|
3.48
|
3.33
|
3.22
|
3.07
|
2.91
|
2.74
|
2.54
|
11
|
4.84
|
3.98
|
3.59
|
3.36
|
3.20
|
3.09
|
2.95
|
2.79
|
2.61
|
2.40
|
12
|
4.75
|
3.88
|
3.49
|
3.26
|
3.11
|
3.00
|
2.85
|
2.69
|
2.50
|
2.30
|
13
|
4.67
|
3.80
|
3.41
|
3.18
|
3.02
|
2.92
|
2.77
|
2.60
|
2.42
|
2.21
|
14
|
4.60
|
3.74
|
3.34
|
3.11
|
2.96
|
2.85
|
2.70
|
2.53
|
2.35
|
2.13
|
15
|
4.54
|
3.68
|
3.29
|
3.06
|
2.90
|
2.79
|
2.64
|
2.48
|
2.29
|
2.07
|
16
|
4.49
|
3.63
|
3.24
|
3.01
|
2.85
|
2.74
|
2.59
|
2.42
|
2.24
|
2.01
|
17
|
4.45
|
3.59
|
3.20
|
2.96
|
2.81
|
2.70
|
2.55
|
2.38
|
2.19
|
1.96
|
18
|
4.41
|
3.55
|
3.16
|
2.93
|
2.77
|
2.66
|
2.51
|
2.34
|
2.15
|
1.92
|
19
|
4.38
|
3.52
|
3.13
|
2.90
|
2.74
|
2.63
|
2.48
|
2.31
|
2.11
|
1.88
|
20
|
4.35
|
3.49
|
3.10
|
2.87
|
2.71
|
2.60
|
2.45
|
2.28
|
2.08
|
1.84
|
21
|
4.32
|
3.47
|
3.07
|
2.84
|
2.68
|
2.57
|
2.42
|
2.25
|
2.05
|
1.81
|
22
|
4.30
|
3.44
|
3.05
|
2.82
|
2.66
|
2.55
|
2.40
|
2.23
|
2.03
|
1.78
|
23
|
4.28
|
3.42
|
3.03
|
2.80
|
2.64
|
2.53
|
2.38
|
2.20
|
2.00
|
1.76
|
24
|
4.26
|
3.40
|
3.01
|
2.78
|
2.62
|
2.51
|
2.36
|
2.18
|
1.98
|
1.73
|
25
|
4.24
|
3.38
|
2.99
|
2.76
|
2.60
|
2.49
|
2.34
|
2.16
|
1.96
|
1.71
|
26
|
4.22
|
3.37
|
2.98
|
2.74
|
2.59
|
2.47
|
2.32
|
2.15
|
1.95
|
1.69
|
27
|
4.21
|
3.35
|
2.96
|
2.73
|
2.57
|
2.46
|
2.30
|
2.13
|
1.93
|
1.67
|
28
|
4.20
|
3.34
|
2.95
|
2.71
|
2.56
|
2.44
|
2.29
|
2.12
|
1.91
|
1.65
|
29
|
4.18
|
3.33
|
2.93
|
2.70
|
2.54
|
2.43
|
2.28
|
2.10
|
1.90
|
1.64
|
30
|
4.17
|
3.32
|
2.92
|
2.69
|
2.53
|
2.42
|
2.27
|
2.09
|
1.89
|
1.62
|
35
|
4.12
|
3.26
|
2.87
|
2.64
|
2.48
|
2.37
|
2.22
|
2.04
|
1.83
|
1.57
|
40
|
4.08
|
3.23
|
2.84
|
2.61
|
2.45
|
2.34
|
2.18
|
2.00
|
1.79
|
1.51
|
45
|
4.06
|
3.21
|
2.81
|
2.58
|
2.42
|
2.31
|
2.15
|
1.97
|
1.76
|
1.48
|
50
|
4.03
|
3.18
|
2.79
|
2.56
|
2.40
|
2.29
|
2.13
|
1.95
|
1.74
|
1.44
|
60
|
4.00
|
3.15
|
2.76
|
2.52
|
2.37
|
2.25
|
2.10
|
1.92
|
1.70
|
1.39
|
70
|
3.98
|
3.13
|
2.74
|
2.50
|
2.35
|
2.23
|
2.07
|
1.89
|
1.67
|
1.35
|
80
|
3.96
|
3.11
|
2.72
|
2.49
|
2.33
|
2.21
|
2.06
|
1.88
|
1.65
|
1.31
|
90
|
3.95
|
3.10
|
2.71
|
2.47
|
2.32
|
2.20
|
2.04
|
1.86
|
1.64
|
1.28
|
100
|
3.94
|
3.09
|
2.70
|
2.46
|
2.30
|
2.19
|
2.03
|
1.85
|
1.63
|
1.26
|
150
|
3.90
|
3.06
|
2.66
|
2.43
|
2.27
|
2.16
|
2.00
|
1.82
|
1.59
|
1.18
|
200
|
3.89
|
3.04
|
2.65
|
2.42
|
2.26
|
2.14
|
1.98
|
1.80
|
1.57
|
1.14
|
300
|
3.87
|
3.03
|
2.64
|
2.41
|
2.25
|
2.13
|
1.97
|
1.79
|
1.55
|
1.10
|
400
|
3.86
|
3.02
|
2.63
|
2.40
|
2.24
|
2.12
|
1.96
|
1.78
|
1.54
|
1.07
|
500
|
3.86
|
3.01
|
2.62
|
2.39
|
2.23
|
2.11
|
1.96
|
1.77
|
1.54
|
1.06
|
1000
|
3.85
|
3.00
|
2.61
|
2.38
|
2.22
|
2.10
|
1.95
|
1.76
|
1.53
|
1.03
|
|
3.84
|
2.99
|
2.60
|
2.37
|
2.21
|
2.09
|
1.94
|
1.75
|
1.52
|
1.00
|
Критические значения t-критерия Стьюдента
при уровне значимости  0.10, 0.05, 0.01. 0.10, 0.05, 0.01.
Число степеней свободы
|
Уровень значимости
|
0.10
|
0.05
|
0.01
|
1
|
6.3138
|
12.706
|
63.657
|
2
|
2.9200
|
4.3027
|
9.9248
|
3
|
2.3534
|
3.1825
|
5.8409
|
4
|
2.1318
|
2.7764
|
4.6041
|
5
|
2.0150
|
2.5706
|
4.0321
|
6
|
1.9432
|
2.4469
|
3.7074
|
7
|
1.8946
|
2.3646
|
3.4995
|
8
|
1.8595
|
2.3060
|
3.3554
|
9
|
1.8331
|
2.2622
|
3.2498
|
10
|
1.8125
|
2.2281
|
3.1693
|
11
|
1.7959
|
2.2010
|
3.1058
|
12
|
1.7823
|
2.1788
|
3.0545
|
13
|
1.7709
|
2.1604
|
3.0123
|
14
|
1.7613
|
2.1448
|
2.9768
|
15
|
1.7530
|
2.1315
|
2.9467
|
16
|
1.7459
|
2.1199
|
2.9208
|
17
|
1.7396
|
2.1098
|
2.8982
|
18
|
1.7341
|
2.1009
|
2.8784
|
19
|
1.7291
|
2.0930
|
2.8609
|
20
|
1.7247
|
2.0860
|
2.8453
|
21
|
1.7207
|
2.0796
|
2.8314
|
22
|
1.7171
|
2.0739
|
2.8188
|
23
|
1.7139
|
2.0687
|
2.8073
|
24
|
1.7109
|
2.0639
|
2.7969
|
25
|
1.7081
|
2.0595
|
2.7874
|
26
|
1.7056
|
2.0555
|
2.7787
|
27
|
1.7033
|
2.0518
|
2.7707
|
28
|
1.7011
|
2.0484
|
2.7633
|
29
|
1.6991
|
2.0452
|
2.7564
|
30
|
1.6973
|
2.0423
|
2.7500
|
40
|
1.6839
|
2.0211
|
2.7045
|
60
|
1.6707
|
2.0003
|
2.6603
|
120
|
1.6577
|
1.9799
|
2.6174
|
|
1.6449
|
1.9600
|
2.5758
|
Значения статистик Дарбина - Уотсона при уровне значимости  . .
n
|
1
|
2
|
3
|
4
|
5
|
dL
|
dU
|
dL
|
dU
|
dL
|
dU
|
dL
|
dU
|
dL
|
dU
|
6
|
0.61
|
1.40
|
-
|
-
|
-
|
-
|
|
|
|
|
7
|
0.70
|
1.36
|
0.47
|
1.90
|
-
|
-
|
|
|
|
|
8
|
0.76
|
1.33
|
0.56
|
1.78
|
0.37
|
2.29
|
|
|
|
|
9
|
0.82
|
1.32
|
0.63
|
1.70
|
0.46
|
2.13
|
|
|
|
|
10
|
0.88
|
1.32
|
0.70
|
1.64
|
0.53
|
2.02
|
|
|
|
|
11
|
0.93
|
1.32
|
0.66
|
1.60
|
0.60
|
1.93
|
|
|
|
|
12
|
0.97
|
1.33
|
0.81
|
1.58
|
0.66
|
1.86
|
|
|
|
|
13
|
1.01
|
1.34
|
0.86
|
1.56
|
0.72
|
1.82
|
|
|
|
|
14
|
1.05
|
1.35
|
0.91
|
1.55
|
0.77
|
1.78
|
|
|
|
|
16
|
1.10
|
1.37
|
0.98
|
1.54
|
0.86
|
1.73
|
0.74
|
1.93
|
0.62
|
2.15
|
17
|
1.13
|
1.38
|
1.02
|
1.54
|
0.90
|
1.71
|
0.78
|
1.90
|
0.67
|
2.10
|
18
|
1.16
|
1.39
|
1.05
|
1.53
|
0.93
|
1.69
|
0.82
|
1.87
|
0.71
|
2.06
|
19
|
1.18
|
1.40
|
1.08
|
1.53
|
0.97
|
1.68
|
0.86
|
1.85
|
0.75
|
2.02
|
20
|
1.20
|
1.41
|
1.10
|
1.54
|
1.00
|
1.68
|
0.90
|
1.83
|
0.79
|
1.99
|
21
|
1.22
|
1.42
|
1.13
|
1.54
|
1.03
|
1.67
|
0.93
|
1.81
|
0.83
|
1.96
|
22
|
1.24
|
1.43
|
1.15
|
1.54
|
1.05
|
1.66
|
0.96
|
1.80
|
0.86
|
1.94
|
23
|
1.26
|
1.44
|
1.17
|
1.54
|
1.08
|
1.66
|
0.99
|
1.79
|
0.90
|
1.92
|
24
|
1.27
|
1.45
|
1.19
|
1.55
|
1.10
|
1.66
|
1.01
|
1.78
|
0.93
|
1.90
|
25
|
1.29
|
1.45
|
1.21
|
1.55
|
1.12
|
1.66
|
1.04
|
1.77
|
0.95
|
1.89
|
26
|
1.30
|
1.46
|
1.22
|
1.55
|
1.14
|
1.65
|
1.06
|
1.76
|
0.98
|
1.88
|
27
|
1.32
|
1.47
|
1.24
|
1.56
|
1.16
|
1.65
|
1.08
|
1.76
|
1.01
|
1.86
|
28
|
1.33
|
1.48
|
1.26
|
1.56
|
1.18
|
1.65
|
1.10
|
1.75
|
1.03
|
1.85
|
29
|
1.34
|
1.48
|
1.27
|
1.56
|
1.20
|
1.65
|
1.12
|
1.74
|
1.05
|
1.84
|
30
|
1.35
|
1.49
|
1.28
|
1.57
|
1.21
|
1.65
|
1.14
|
1.74
|
1.07
|
1.83
|
Темы рефератов
Модель ценообразования на основной капитал: применение парного регрессионного анализа.
Диверсификация и оптимальность портфеля ценных бумаг: эконометрический подход.
Вывод функций издержек, основанный на производственной функции Кобба-Дугласа.
Анализ взаимосвязи между ценой и качеством
Применение гедонического метода к индексу цен на компьютеры
Издержки, кривые обучения и эффект масштаба: от парной регрессии к множественной.
Измерение изменения качества: построение гедонического индекса цен
Функциональные формы для статистических функций заработков
Подходы к определению и оценке влияния дискриминации на заработную плату
Моделирование нормы отдачи от образования.
Исследование зависимости доходов от профессионального опыта
Авторегрессионная модель временных рядов для совокупных инвестиций
Эконометрические модели спроса на электроэнергию
Влияние изменений в совокупном спросе на предложение труда

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«Дальневосточный федеральный университет»
(ДВФУ)

филиал двфу в г. спасске-дальнем
|
|
|
 Скачать 1.23 Mb.
Скачать 1.23 Mb.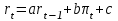 . Исходные данные можно взять на сайтах http://www.finam.ru/analysis/macroevent/default.asp, www.hse.ru, www.cbr.ru. Проведите анализ и сделайте вывод.
. Исходные данные можно взять на сайтах http://www.finam.ru/analysis/macroevent/default.asp, www.hse.ru, www.cbr.ru. Проведите анализ и сделайте вывод.
