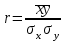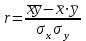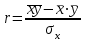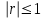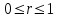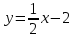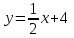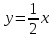ЕН.Ф.4 Эконометрика. Лекции 17 (час.) практические занятия 17 час семинарские занятия час лабораторные работы час
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫпо дисциплине«Эконометрика»Специальность 080105.65 «Финансы и кредит» г. Спасск-Дальний 2012 Вопросы к экзамену Предмет, метод и задачи эконометрики. Связь эконометрики с экономической теорией, математической и экономической статистикой. Эконометрический метод. Эконометрическая модель. Типы моделей. Типы данных. Основные этапы эконометрического моделирования. Компьютеры и эконометрическая практика. Модель парной линейной регрессии. Метод наименьших квадратов. Интерпретация коэффициентов уравнения регрессии. Экономическая интерпретация коэффициентов уравнения регрессии. Линейный коэффициент корреляции как показатель тесноты связи между явлениями. Коэффициент детерминации. Показатели качества регрессии. Закон Оукена как пример парной линейной регрессии в экономике. Нелинейная парная регрессия на основе метода наименьших квадратов. Нелинейные регрессионные модели: степенная, показательная, гиперболическая, параболическая. Линеаризация нелинейных моделей. Выбор лучшей модели. Индекс корреляции нелинейной регрессии. Индекс детерминации. Коэффициент эластичности. Оценка влияния трудоемкости, объема производства, цен на энергоресурсы, налогов на себестоимость единицы продукции. Последствия для свойств МНК-оценки. Вывод альтернативной оценки. Гетероскедастичность и ее последствия. Тесты на гетероскедастичность. Пример: объяснение спроса на рабочую силу. Устранение гетероскедастичности. Взвешенный метод наименьших квадратов. Автокорреляция первого порядка. Тестирование на наличие автокорреляции. Пример: спрос на мороженое. Неправильная спецификация модели. Пример: рисковая премия на валютных рынках. Построение линейной множественной регрессии. Вывод и интерпретация коэффициентов множественной регрессии. Индекс множественной корреляции. Индекс множественной детерминации. Мультиколлинеарность. Отбор наиболее существенных факторных признаков в уравнении регрессии. Проверка мультиколлинеарности методом испытания гипотезы о независимости переменных. Применение линейных множественных регрессий в ценообразовании. Множественная регрессия в нелинейных моделях. Типы нелинейных моделей. Производственные функции. Моделирование производственной функции Кобба-Дугласа, связывающей объем выпуска с капитальными вложениями и затратами труда. Оценка коэффициентов уравнения регрессии и тесноты связи в ППП MS Excel. Инструменты анализа данных «Регрессия», «Корреляция». Теорема Гаусса-Маркова. Оценка значимости коэффициентов парной и множественной регрессионной модели. t-критерий Стьюдента. Оценка значимости уравнения парной и множественной регрессии. F – критерий Фишера. Принятие решения на основе уравнения регрессии. Определение доверительных интервалов для коэффициентов и функции регрессии. Фиктивные переменные. Бинарные фиктивные переменные. Преимущество использования бинарных фиктивных переменных. Уравнение регрессии с фиктивной переменной. Интерпретация коэффициентов. Использование сезонных фиктивных переменных в модели потребления электроэнергии. Выбор эталонной переменной. Множественные совокупности фиктивных переменных. Пример зависимости веса новорожденного от показателя курения и фиктивных переменных: пола, первый или нет ребенок. Фиктивные переменные для коэффициента наклона. Тест Чоу. Модельные примеры: влияет ли пол на уровень успеваемости студентов, одинакова ли в крупных и мелких странах зависимость военных расходов от ВВП. Модели бинарного выбора. Спецификационные тесты в моделях бинарного вывода. Модели с множественным откликом. Пример: готовность платить за природные области, не затрагиваемые деятельностью человека. Тобит-модель. Логит-модель. Временной ряд. Модели стационарных и нестационарных временных рядов. Модель с включением фактора времени. Автокорреляция остатков временного ряда. Положительная и отрицательная автокорреляция. Тесты на наличие автокорреляции. Устранение автокорреляции. Обобщенный метод наименьших квадратов. Уравнение авторегрессии. Модельный пример авторегрессии: зависимость объемов продаж от объемов продаж в предыдущие моменты времени и расходов на рекламу. Метод инструментальной переменной. Коинтеграция временных рядов. Тест Энгеля-Грэнжера. Модели с распределенными лагами. Лаги Алмон. Общий вид системы одновременных уравнений. Типы систем уравнений. Модель производительности труда и фондоотдачи. Модель динамики цен и заработной платы. Модель экономической эффективности сельскохозяйственного производства. Эндогенные, экзогенные, предопределенные переменные. Проблемы идентифицируемости. Правило идентифицируемости. Структурная форма модели. Приведенная форма модели. Косвенный метод наименьших квадратов. Двухшаговый и трехшаговый метод наименьших квадратов. Преимущества панельных данных. Эффективность оценивания параметров. Идентификация параметров. Модель с фиксированными эффектами. Модели со случайными эффектами. Качество подгонки данных моделью. Альтернативные оценки метода инструментальных переменных. Тестирование на наличие гетероскедастичности и автокорреляции. Пример: объяснение индивидуальной заработной платы. Динамические линейные модели. Модель авторегрессии панельных данных. Неполные панельные данные. Тесты по теме «Парная регрессия и корреляция» Вопрос 1. Парной регрессией называется уравнение связи
Вопрос 2. Различают
Вопрос 3. Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции для линейной регрессии:
Вопрос 4. Коэффициент корреляции изменяется в пределах
Вопрос 5. О чем говорит коэффициент корреляции, равный 0.8?
Вопрос 6. Степенная функция 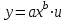 относится к относится к
Вопрос 7. Соотношение 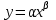 может быть преобразовано в линейное уравнение путем использования может быть преобразовано в линейное уравнение путем использования
Вопрос 8. Тесноту связи изучаемых явлений для нелинейных регрессий оценивает
Вопрос 9. Долю изменения результативного признака за счет изменения факторных характеризует
Вопрос 10. Пусть получено следующее уравнение регрессии 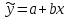 , где x и y – переменные с простыми естественными единицами измерения. Как проинтерпретировать параметр b? , где x и y – переменные с простыми естественными единицами измерения. Как проинтерпретировать параметр b?
Вопрос 11. Пусть получено следующее уравнение регрессии 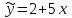 , где x и y – переменные с простыми естественными единицами измерения. Как проинтерпретировать параметр при объясняющей переменной? , где x и y – переменные с простыми естественными единицами измерения. Как проинтерпретировать параметр при объясняющей переменной?
Вопрос 12. Если 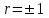 , то это является необходимым и достаточным условием того, чтобы y и x были связаны , то это является необходимым и достаточным условием того, чтобы y и x были связаны
Вопрос 13. При 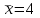 , , 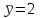 , , 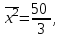 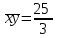 как будет выглядеть уравнение регрессии? как будет выглядеть уравнение регрессии?
Вопрос 14. Гетероскедастичность – условие «неодинакового разброса», т.е.
Вопрос 15. Оценивание качества уравнения регрессии, состоящее в проверке гипотезы 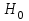 о статистической незначимости уравнения регрессии, происходит на основе о статистической незначимости уравнения регрессии, происходит на основе
Вопрос 16. Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются
|