ЕН.Ф.4 Эконометрика. Лекции 17 (час.) практические занятия 17 час семинарские занятия час лабораторные работы час
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
|
Тема 7. Модели с ограниченными зависимыми переменными Учебные вопросы: Модели бинарного выбора. Спецификационные тесты в моделях бинарного вывода. Модели с множественным откликом. Мультиномиальные модели. Тобит-модель. Логит-модель. Рассмотрим моделирование с ограниченными зависимыми переменными в приложении к оценке финансового состояния предприятия. Для оценки финансово-экономического состояния предприятий возникают ситуации, для описания которых удобно использовать дихотомические (бинарные) результативные показатели, т. е. такие, которые могут принимать только два значения: «0» или «1». Наиболее распространенными моделями бинарного выбора являются logit-модели.
Результаты зарубежной практики в области финансового менеджмента показывают, что от использования моделей оценки риска банкротства, основанных на дискриминантном анализе практически полностью отказались, и все больше внимания стало уделяться другим, более современным эконометрическим инструментам и, прежде всего, так называемым logit-моделям. Такие модели применяют, когда переменная латентна (скрытая) и ее невозможно оценить при помощи обычной многофакторной регрессии. В статистике логистическая регрессия – модель, используемая для предсказания вероятности возникновения события «подгоном» данных к логистической кривой. При этом используют несколько предсказывающих переменных, которые могут быть или числовыми или категориальными. Logit-модель относится к классу таких моделей, для анализа которых неприменимы обычные методы регрессионного анализа. Отличие ее состоит в том, что в ней зависимая переменная может принимать лишь ограниченное число значений, в простейшем случае – либо 0, либо 1. Задача состоит в том, чтобы определить вероятность принятия зависимой переменной значения 0 или 1. Здесь в качестве аналитического средства применяется логистическая функция, поэтому logit-модели часто называют моделями логистической регрессии. Другие названия для логистической регрессии, используемые в различных прикладных областях, включают логистическую модель, logit-модель, и классификатор максимальной энтропии. Кроме того, logit-модель позволяет учитывать не только количественные, но и качественные переменные. Изначальным источником logit было приложение вероятностных моделей к биологическим опытам бинарного выбора в первой половине прошлого века, а термин «logit» был впервые использован Берксоном в 1944 г. Впервые для целей прогнозирования несостоятельности logit-модель была применена Мартином в 1977 г., однако это была модель прогнозирования банкротства кредитных организаций. Первой моделью прогнозирования состояния предприятий, использующей logit-анализ, была модель Олсона, разработанная в 1980 г. Logit-модель, представлена следующей функцией: 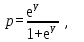 где p является комплексным критерием вероятности банкротства предприятия; е – математическая константа (константа Эйлера), которая является основанием натурального логарифма и составляет порядка 2,718; y – результативный показатель (вероятность наступления банкротства предприятия). где p является комплексным критерием вероятности банкротства предприятия; е – математическая константа (константа Эйлера), которая является основанием натурального логарифма и составляет порядка 2,718; y – результативный показатель (вероятность наступления банкротства предприятия).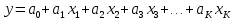 , , где а0 называют «точкой пересечения», это постоянная величина результативного показателя, которая не связана с изменением факторов; а1, а2, а3 и т. д. называют «коэффициентами регрессии» для управляющих параметров (факторов вероятности банкротства), они показывают среднее изменение результативного показателя с повышением или понижением величины фактора на единицу его измерения; х1, х2, х3 – факторные показатели. Положительный коэффициент регрессии означает, что данный фактор увеличивает общий риск (т.е. повышает вероятность анализируемого исхода), в то время как отрицательный коэффициент означает, что этот фактор уменьшает риск; большой коэффициент регрессии означает, что данный фактор существенно влияет на совокупный риск, в то время как почти нулевой коэффициент регрессии означает, что этот фактор имеет небольшое влияние на вероятность результата. Ряд исследований, проведенных С. Ленноксом, показал, что на практике logit-модели позволяют получить значительно более эффективные оценки риска банкротства, чем теоретически может обеспечить дискриминантный анализ (MDA). Более того, использование logit-регрессии предполагает широкие возможности для проведения разнообразных эконометрических тестов, которые позволяют оценить статистическую значимость как модели в целом, так и отдельных переменных, которые ее формируют. При этом в отличие от MDA, logit-регрессия позволяет не только сделать вывод относительно принадлежности предприятия к группе потенциальных банкротов (чем ограничивается интерпретация результатов расчетов с использованием моделей, построенных на основе MDA), но и оценить риск банкротства предприятия по количественной шкале. В российской практике данные модели не нашли применения, несмотря на тот факт, что их использование позволяет дать ответы на вопросы, которые были неразрешимы с помощью методов дискриминантного анализа. Исследования зарубежных logit-моделей оценки риска банкротства на предмет возможности применения в российской практике финансового менеджмента, по которым подобный анализ ранее не проводился, показали, что данные модели представляют значительный интерес с точки зрения использования на отечественных предприятиях, поскольку показали высокую точность в странах, где были разработаны. Точность оценки риска банкротства предприятий на основе исследуемых logit-моделей зарубежных авторов представлена в таблице. Таблица – Точность оценки риска банкротства по результатам апробации logit-моделей зарубежных авторов
Как видно из таблицы, точность оценки риска банкротства по результатам исследования зарубежных logit-моделей является достаточно низкой (несмотря на тот факт, что точность оценки риска банкротства в странах, где данные модели были разработаны, превышает 80%). Более того, оценки риска банкротства, полученные на их основе, не позволяют сделать однозначный вывод относительно вероятности банкротства предприятий, вошедших в выборку: расчеты дают неверные (часто обратные) результаты. Дополнительно: эффективная оценка риска банкротства в современной практике финансового менеджмента на предприятии, источник: http://chief.viperson.ru/wind.php?ID=601029&soch=1. Вопросы для самопроверки: Модели бинарного выбора. Применение на практике. Модели с множественным откликом. Пример: готовность платить за природные области, не затрагиваемые деятельностью человека. Логит-модель. Оценка риска банкротства в современной практике финансового менеджмента с помощью логит-модели. Тема 8. Моделирование динамических процессов Учебные вопросы: Временной ряд. Модели стационарных и нестационарных временных рядов. Модель с включением фактора времени. Автокорреляция остатков временного ряда. Положительная и отрицательная автокорреляция. Тесты на наличие автокорреляции. Устранение автокорреляции. Обобщенный метод наименьших квадратов. Уравнение авторегрессии. Метод инструментальной переменной. Коинтеграция временных рядов. Тест Энгеля-Грэнжера. Модели с распределенными лагами. Лаги Алмон. Использование фиктивных переменных в моделировании сезонных колебаний. Под временным рядом в экономике понимается последовательность наблюдений некоторого признака (случайной величины) Y в последовательные моменты времени. Отдельные наблюдения называются уровнями ряда и обозначаются 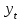 . . В статистике переменная t - время выступала в качестве факторного признака: 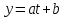 , а коэффициенты определялись по формулам: , а коэффициенты определялись по формулам: 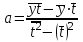 , , 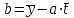 . Рассмотрим регрессионную модель временного ряда. Если в модели результаты предыдущих наблюдений влияют на результаты последующих, то такие модели называются моделями с наличием автокорреляции. . Рассмотрим регрессионную модель временного ряда. Если в модели результаты предыдущих наблюдений влияют на результаты последующих, то такие модели называются моделями с наличием автокорреляции. Рассмотрим временной ряд – ряд последовательных значений курса ценной бумаги в моменты времени от 1 до 278. Результаты наблюдений можно графически представить в виде: 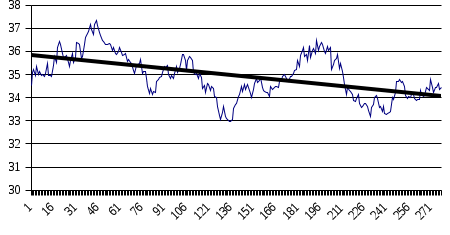 Курс ценной бумаги имеет тенденцию к снижению, это видно из графика. Оценивая обычным МНК зависимость курса акции от времени получим: 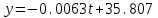 . Естественно предположить, что результаты предыдущих торгов оказывают на результаты последующих: если в какой-то момент времени курс окажется завышенным по сравнению с реальным, то скорее всего он будет и завышен на следующих торгах, т.е. имеет место положительная автокорреляция. Графически положительная автокорреляция выражается в чередовании зон, где наблюдаемые значения оказываются выше расчетных и зон, где наблюдаемые значения ниже. . Естественно предположить, что результаты предыдущих торгов оказывают на результаты последующих: если в какой-то момент времени курс окажется завышенным по сравнению с реальным, то скорее всего он будет и завышен на следующих торгах, т.е. имеет место положительная автокорреляция. Графически положительная автокорреляция выражается в чередовании зон, где наблюдаемые значения оказываются выше расчетных и зон, где наблюдаемые значения ниже. Отрицательная автокорреляция встречается в тех случаях, когда наблюдения действуют друг на друга по принципу маятника – завышенные значения в предыдущих наблюдениях приводят к занижению их в наблюдениях последующих. Графически это выражается в том, что результаты наблюдений «слишком часто» перескакивают график регрессии. В случае наличия автокорреляции коэффициенты регрессии оказываются заниженными и результаты тестирований гипотез оказываются недостоверными. Если рассматривается ряд значений курса ценной бумаги, то результат последних торгов служит отправной точкой для формирования курса на следующих торгах. Можно предположить наличие корреляция между соседними членами. Тест на наличие автокорреляции между соседними членами – тест Дарбина-Уотсона состоит в следующем. Рассчитывается статистика Дарбина-Уотсона: 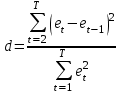 . .Существует известная взаимосвязь между данной статистикой и коэффициентом корреляции:  . По таблицам значений статистик Дарбина-Уотсона определяются границы . По таблицам значений статистик Дарбина-Уотсона определяются границы 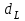 и и  при числе наблюдений n и числе факторных признаков k. Определяется, какому интервалу принадлежит d: при числе наблюдений n и числе факторных признаков k. Определяется, какому интервалу принадлежит d:если 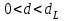 , то имеет место положительная автокорреляция, , то имеет место положительная автокорреляция,если 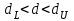 , то невозможно решить вопрос о наличии автокорреляции, , то невозможно решить вопрос о наличии автокорреляции,если 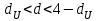 , то автокорреляция отсутствует, , то автокорреляция отсутствует,если 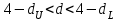 , то невозможно решить вопрос о наличии автокорреляции, , то невозможно решить вопрос о наличии автокорреляции,если 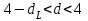 , то имеет место отрицательная автокорреляция. , то имеет место отрицательная автокорреляция.При наличии автокорреляции нельзя оценивать коэффициенты регрессии обычным методом наименьших квадратов. Рассмотрим модель 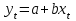 , при t-1 эта модель примет вид: , при t-1 эта модель примет вид: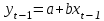 Домножим это уравнение на 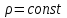 : : 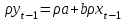 . .Вычтем из модели для времени t модель для t-1 и упростим ее: 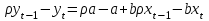 ; ;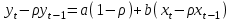 Заменим: 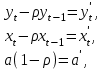 получим 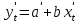 . Для оценки параметров . Для оценки параметров 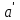 и и 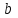 в этой регрессии можно применить обычный метод наименьших квадратов. в этой регрессии можно применить обычный метод наименьших квадратов. Итак, если исходное уравнение содержит автокорреляцию, то для оценки его параметров используют обобщенный метод наименьших квадратов, этапы которого следующие: Преобразовать исходные временные ряды 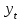 и и 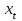 к к 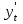 и и  . .Применить обычный метод наименьших квадратов к уравнению 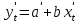 , рассчитать оценки , рассчитать оценки 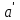 и и 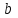 . .Рассчитать а по формуле: 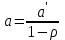 . .Записать исходное уравнение 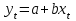 Основная проблема, связанная с применением данного метода состоит в том, как получить оценку r. Основным способом является получение оценки по исходному уравнению регрессии исходя из следующего соотношения: 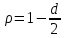 , где d – статистика Дарбина-Уотсона. , где d – статистика Дарбина-Уотсона.Рассмотрим уравнение 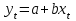 . Если построить динамики явлений . Если построить динамики явлений 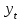 и и 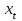 , то можно выяснить, имеет ли место одинаковая направленность тенденций. Если это наблюдается на протяжении длительного промежутка времени, то это значит, что коэффициент корреляции, рассчитанный по уровням временных рядов, может соответственно не содержать ложной корреляции и характеризовать истинную причинно-следственную зависимость между ними. , то можно выяснить, имеет ли место одинаковая направленность тенденций. Если это наблюдается на протяжении длительного промежутка времени, то это значит, что коэффициент корреляции, рассчитанный по уровням временных рядов, может соответственно не содержать ложной корреляции и характеризовать истинную причинно-следственную зависимость между ними.Эти предположения были положены в основу теории коинтеграции временных рядов. Коинтерграция – причинно-следственная зависимость в уровнях двух (и более) временных рядов, которая выражается в совпадении или противоположной направленности их тенденций и колеблемости. Существует тест на проверку коинтеграции временных рядов. Это тест Энгеля-Грэнжера, за который в 2003 году была присуждена Нобелевская премия по экономике. Этапы проведения теста: Рассчитывается регрессия 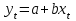 . Вычисляются остатки . Вычисляются остатки 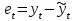 . .Вычисляется регрессия 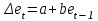 . .Определяется фактическое значение t-критерия для коэффициента регрессии b. Если tрасч для коэффициента b больше критических значений, то имеет место коинтеграция.
Динамической называется модель, если она отражает динамику исследуемых переменных в каждый момент времени. К основным типам динамических эконометрических моделей относятся модели с распределенным лагом и модели авторегрессии. Модель с распределенным лагом имеет вид: 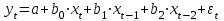 Наряду с лаговыми значениями независимых, или факторных, переменных на величину зависимой переменной текущего периода могут оказывать влияние ее значения в прошлые моменты или периоды времени. Эти процессы обычно описывают с помощью моделей регрессии, содержащих в качестве факторов лаговые значения зависимой переменной, которые называются моделями авторегрессии. Модель вида 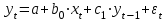 относится к моделям авторегрессии. Рассмотрим модель с распределенным лагом в ее общем виде в предположении, что максимальная величина лага конечна: 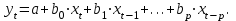 Эта модель говорит о том, что если в некоторый момент времени t происходит изменение независимой переменной х, то это изменение будет влиять на значения переменной у в течение p следующих моментов времени. Коэффициенты 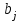 могут быть представлены в виде полиномов: могут быть представлены в виде полиномов:• для полинома 1-й степени: 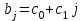 ; ;• для полинома 2-й степени: 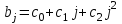 ; ;• для полинома 3-й степени: 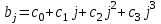 и т. д. и т. д.Тогда каждый из коэффициентов 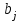 можно выразить следующим образом: можно выразить следующим образом: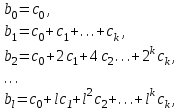 Подставив в уравнение эти коэффициенты и перегруппировав слагаемые, получим: 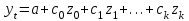 , ,где 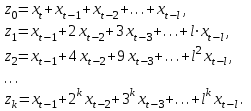 Процедура применения метода Алмон для расчета параметров модели с распределенным лагом выглядит следующим образом. Определяется максимальная величина лага l. Определяется степень полинома k, описывающего структуру лага. По соотношениям рассчитываются значения переменных 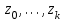 . .Определяются параметры уравнения линейной регрессии 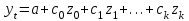 . .С помощью соотношений рассчитываются параметры исходной модели с распределенным лагом. Проинтерпретируем коэффициенты в модели с распределенными лагами. Коэффициент регрессии 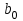 при переменной при переменной 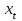 характеризует среднее абсолютное изменение характеризует среднее абсолютное изменение 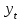 при изменении при изменении 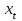 на 1 ед. своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором. на 1 ед. своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.В момент времени t+1 совокупное воздействие факторной переменной х, на результат у составит 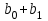 ед., в момент t+2 это воздействие можно охарактеризовать суммой ед., в момент t+2 это воздействие можно охарактеризовать суммой 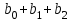 т. д. Полученные таким образом суммы называют промежуточными мультипликаторами. т. д. Полученные таким образом суммы называют промежуточными мультипликаторами.С учетом конечной величины лага можно сказать, что изменение переменной 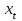 , в момент t на 1 ед. приведет к общему изменению результата , в момент t на 1 ед. приведет к общему изменению результата 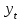 через p моментов времени на через p моментов времени на 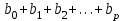 абсолютных единиц. Эту величину называют долгосрочным мультипликатором. Он показывает абсолютное изменение в долгосрочном периоде t+1 результата под влиянием изменения на 1 ед. фактора х. абсолютных единиц. Эту величину называют долгосрочным мультипликатором. Он показывает абсолютное изменение в долгосрочном периоде t+1 результата под влиянием изменения на 1 ед. фактора х.Пусть 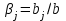 . Это относительные коэффициенты модели с распределенным лагом. Если все коэффициенты имеют одинаковые знаки, то . Это относительные коэффициенты модели с распределенным лагом. Если все коэффициенты имеют одинаковые знаки, то 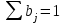 . В этом случае относительные коэффициенты являются весами для соответствующих коэффициентов. Каждый из них измеряет долю общего изменения результативного признака в момент времени t+j. Средний лаг определяется по формуле средней арифметической взвешенной: . В этом случае относительные коэффициенты являются весами для соответствующих коэффициентов. Каждый из них измеряет долю общего изменения результативного признака в момент времени t+j. Средний лаг определяется по формуле средней арифметической взвешенной: 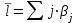 и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени t. Небольшая величина среднего лага свидетельствует об относительно быстром реагировании результата на изменение фактора, тогда как высокое его значение говорит о том, что воздействие фактора на результат будет сказываться в течение длительного периода времени. Медианный лаг – это величина лага, для которого 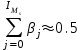 . Это тот период времени, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат. . Это тот период времени, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат.Модель авторегрессии имеет вид: 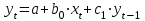 . Одним из возможных методов расчета параметров уравнения авторегрессии является метод инструментальных переменных. Сущность этого метода состоит в том, чтобы заменить переменную из правой части модели, для которой нарушаются предпосылки метода наименьших квадратов, на новую переменную, включение которой в модель регрессии не приводит к нарушению его предпосылок. Применительно к моделям авторегрессии необходимо удалить из правой части модели переменную . Одним из возможных методов расчета параметров уравнения авторегрессии является метод инструментальных переменных. Сущность этого метода состоит в том, чтобы заменить переменную из правой части модели, для которой нарушаются предпосылки метода наименьших квадратов, на новую переменную, включение которой в модель регрессии не приводит к нарушению его предпосылок. Применительно к моделям авторегрессии необходимо удалить из правой части модели переменную 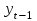 . Искомая новая переменная, которая будет введена в модель вместо . Искомая новая переменная, которая будет введена в модель вместо 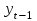 , должна иметь два свойства. Во-первых, она должна тесно коррелировать с , должна иметь два свойства. Во-первых, она должна тесно коррелировать с 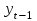 , во-вторых, она не должна коррелировать с остатками , во-вторых, она не должна коррелировать с остатками 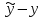 . .Поскольку в модели переменная 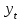 , зависит не только от , зависит не только от 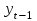 , но и от , но и от 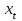 можно предположить, что имеет место зависимость можно предположить, что имеет место зависимость 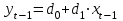 . Расчетное значение . Расчетное значение 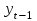 может служить в качестве инструментальной переменной для фактора может служить в качестве инструментальной переменной для фактора 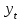 . Таким образом, оценки параметров уравнения . Таким образом, оценки параметров уравнения 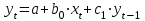 можно найти из соотношения можно найти из соотношения 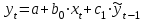 . .Как и в модели с распределенным лагом, 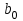 в этой модели характеризует краткосрочное изменение у, под воздействием изменения х на 1 ед. К моменту времени t+1 результат у, изменился под воздействием изменения изучаемого фактора в момент времени t на в этой модели характеризует краткосрочное изменение у, под воздействием изменения х на 1 ед. К моменту времени t+1 результат у, изменился под воздействием изменения изучаемого фактора в момент времени t на 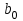 ед., а ед., а  под воздействием своего изменения в непосредственно предшествующий момент времени — на под воздействием своего изменения в непосредственно предшествующий момент времени — на 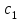 ед. Таким образом, общее абсолютное изменение результата в момент t+1 составит ед. Таким образом, общее абсолютное изменение результата в момент t+1 составит 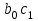 ед. Аналогично в момент времени t+2 абсолютное изменение результата составит ед. Аналогично в момент времени t+2 абсолютное изменение результата составит 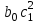 ед. и т. д. Следовательно, долгосрочный мультипликатор в модели авторегрессии можно рассчитать как сумму краткосрочного и промежуточных мультипликаторов: ед. и т. д. Следовательно, долгосрочный мультипликатор в модели авторегрессии можно рассчитать как сумму краткосрочного и промежуточных мультипликаторов: Поскольку практически все модели авторегрессии имеют так называемое условие стабильности, состоящее в том, что коэффициент регрессии при переменной 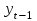 по абсолютной величине меньше единицы то b можно преобразовать следующим образом: по абсолютной величине меньше единицы то b можно преобразовать следующим образом: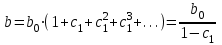 где |c1| < 1. Вопросы для самопроверки: Модель с включением фактора времени. Дайте понятие автокорреляции остатков временного ряда. Как обнаружить и устранить автокорреляцию. Этапы обобщенного метода наименьших квадратов. Модельный пример авторегрессии: зависимость объемов продаж от объемов продаж в предыдущие моменты времени и расходов на рекламу. Этапы метода инструментальной переменной. Коинтеграция временных рядов. Тест Энгеля-Грэнжера. Модели с распределенными лагами. Лаги Алмон. Использование фиктивных переменных в моделировании сезонных колебаний. Тема 9. Системы эконометрических уравнений Учебные вопросы: Общий вид системы одновременных уравнений. Типы систем уравнений. Эндогенные, экзогенные, предопределенные переменные. Проблемы идентифицируемости. Правило идентифицируемости. Структурная форма модели. Приведенная форма модели. Косвенный метод наименьших квадратов. Двухшаговый и трехшаговый метод наименьших квадратов. Сложные экономические процессы описывают с помощью системы взаимосвязанных (одновременных) уравнений. Существуют следующие виды систем уравнений: 1. Система независимых уравнений – когда каждая зависимая переменная y рассматривается как функция одного и того же набора факторов x: 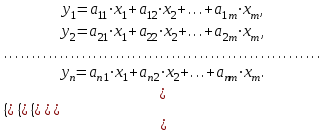 Для решения этой системы и нахождения ее параметров используется метод наименьших квадратов. Каждое уравнение может рассматриваться самостоятельно. Пример – модель экономической эффективности сельскохозяйственного производства. Зависимые переменные – показатели, характеризующие эффективность сельскохозяйственного производства – продуктивность коров, себестоимость молока, а в качестве факторов берутся специализация хозяйства, затраты труда, количество голов на 100 га пашни. 2. Система рекурсивных уравнений – когда зависимая переменная y одного уравнения выступает в виде фактора x в другом уравнении 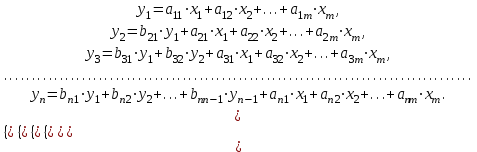 Зависимая переменная включается в каждое последующее уравнение. Каждое уравнение может рассматриваться отдельно, для решения этой системы и нахождения ее параметров используется метод наименьших квадратов; примером может быть модель производительности труда и фондоотдачи, когда производительность зависит от фондовооруженности, энерговооруженности, квалификации рабочих, а фондоотдача – еще и от производительности труда. 3. Система взаимосвязанных (совместных) уравнений – когда одни и те же переменные в одних уравнениях входят в левую часть, а в других – в правую: 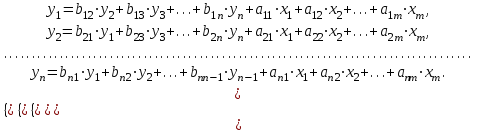 Такая система уравнений называется структурной формой модели. Отдельно каждое уравнение рассматриваться не может и для этой системы не применим обычный метод наименьших квадратов. Пример – модель динамики цен и заработной платы, где темп изменения месячной зарплаты зависит от темпа изменения цен и процента безработных, а темп изменения цен - от темпа месячной зарплаты, темпа изменения постоянного капитала и от изменения цен на импорт сырья. Структурная форма модели 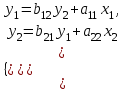 содержит эндогенные переменные – взаимозависимые переменные, которые определяются внутри модели (системы), а также экзогенные переменные – независимые переменные, которые определяются вне системы. Предопределенные переменные – экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные системы. Коэффициенты содержит эндогенные переменные – взаимозависимые переменные, которые определяются внутри модели (системы), а также экзогенные переменные – независимые переменные, которые определяются вне системы. Предопределенные переменные – экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные системы. Коэффициенты 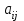 и и 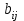 при переменных – структурные коэффициенты модели. при переменных – структурные коэффициенты модели.Система линейных функций эндогенных переменных от всех предопределенных переменных системы – приведенная форм модели: 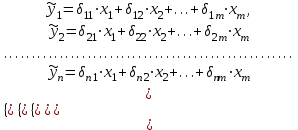 где 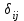 - коэффициенты приведенной формы модели. Эта система может быть получена из структурной формы модели путем алгебраических преобразований. - коэффициенты приведенной формы модели. Эта система может быть получена из структурной формы модели путем алгебраических преобразований.При переходе от структурной формы модели к приведенной форме возникает проблема идентификации – единственности соответствия между приведенной и структурной формами модели. С этой точки зрения существует три вида моделей: идентифицируемые, неидентифицируемые, сверхидентифицируемые. Модель идентифицируема, если число параметров структурной модели равно числу параметров приведенной формы модели. Модель неидентифицируема, если число параметров структурной модели больше числа параметров приведенной формы модели. Модель сверхидентифицируема, если число параметров структурной модели меньше числа параметров приведенной формы модели. Для определения типа модели необходимо рассматривать каждое уравнение, так, если каждое уравнение идентифицируемо, то и модель идентифицируема. Если хотя бы одно уравнение в системе неидентифицируемо, то и вся модель считается неидентифицируемой. Модель считается сверхиндентифицируемой, если хотя бы одно уравнение сверхидентифицируемо. Если обозначить через H-число эндогенных переменных в уравнении, через D-число экзогенных переменных, отсутствующих в уравнении, но присутствующих в системе, то условие идентифицируемости модели может быть записано в виде правила: D+1=H – уравнение идентифицируемо; D+1<H – уравнение неидентифицируемо; D+1>H – уравнение сверхидентифицируемо. Для решения идентифицируемого уравнения применяется косвенный метод наименьших квадратов, для решения сверхидентифицируемых уравнений косвенный метод наименьших квадратов применим быть не может, поскольку дает неоднозначные оценки коэффициентов. Для таких уравнений применяют двухшаговый метод наименьший квадратов. Косвенный МНК состоит в следующем: Составляют приведенную форму модели и определяют численные значения параметров ее уравнения обычным МНК; Путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров. Двухшаговый МНК заключается в следующем: Составляют приведенную форму модели и определяют численные значения параметров каждого ее уравнения обычным МНК; Выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяют двухшаговым МНК, и находят расчетные значения по соответствующим уравнениям приведенной формы модели; Обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения. Рассмотрим пример. Имеются данные, характеризующие годовое потребление мяса на душу населения, средние потребительские цены, среднедушевые денежные доходы, индекс цен производителей по Приморскому краю.
Построим модель вида 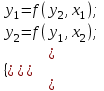 рассчитав соответствующие структурные коэффициенты модели. рассчитав соответствующие структурные коэффициенты модели.Рассматриваемая система – это система взаимозависимых уравнений, поэтому искомая система уравнений будет иметь вид: 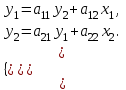 Сначала определим идентифицируема ли система уравнений, для этого определим идентифицируемо ли каждое уравнение: число всех эндогенных переменных Н=2, D=1, D+1=H, значит уравнение идентифицировано. Для второго уравнения: Н=2, D=1 D+1=Н 1+1=2 уравнение идентифицировано. Вся система идентифицируема. Следовательно, для определения параметров этой системы воспользуемся косвенным методом наименьших квадратов. Запишем приведенную систему уравнений, коэффициенты которой оцениваем обычным методом наименьших квадратов: 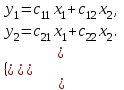 Для оценки коэффициентов регрессии с нулевой константой в качестве исходных данных возьмем отклонения от средних:
Решим систему уравнений:  Подставим в уравнение для у1 данные и решим его
 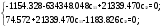 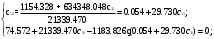 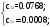 Подставим в уравнение для у2 данные и решим его:
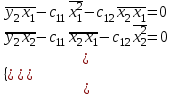 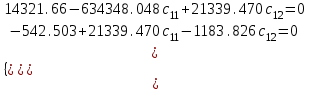 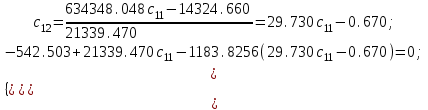 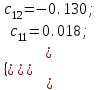 Подставим полученные значения в исходное уравнение (1): 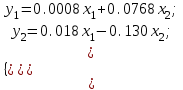 Из приведенной формы можем определить коэффициенты структурной модели, для этого выразим из первого уравнения х1 и подставим во второе уравнение, в результате получим уравнение: 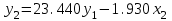 Выразим из второго уравнения х2 и подставим в первое и получим уравнение: 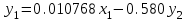 Итак, структурная форма модели имеет вид: 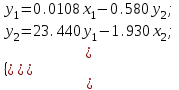 Проинтерпретируем коэффициенты. Первое уравнение показывает, что при увеличении среднедушевых доходов населения на 100 рублей, годовое потребление мяса возрастает на 1,08 кг, а при увеличении средней потребительской цены на мясо на 1 рубль, годовое потребление мяса снижается на 0,58 кг. Второе уравнение показывает, что при увеличении годового потребления мяса на 1 кг, средние потребительские цены возрастают на 23,44 рубля, а при увеличении индекса цен производителей на 1 %, средние потребительские цены снижаются на 1,963 рубля. Вопросы для самопроверки: Системы одновременных уравнений и их типы. Модель производительности труда и фондоотдачи. Модель динамики цен и заработной платы. Модель экономической эффективности сельскохозяйственного производства. Проблемы идентифицируемости. Правило идентифицируемости. Структурная форма модели. Приведенная форма модели. Этапы косвенного метода наименьших квадратов. Этапы двухшагового и трехшагового метода наименьших квадратов. Тема 10. Модели, основанные на панельных данных Учебные вопросы: Преимущества панельных данных. Эффективность оценивания параметров. Идентификация параметров. Статическая линейная модель. Модель с фиксированными эффектами. Модели со случайными эффектами. Качество подгонки данных моделью. Альтернативные оценки метода инструментальных переменных. Тестирование на наличие гетероскедастичности и автокорреляции. Пример: объяснение индивидуальной заработной платы. Динамические линейные модели. Модель авторегрессии панельных данных. Неполные панельные данные. С курсом «Введение в эконометрический анализ панельных данных» можно ознакомиться по ссылке: http://ecsocman.hse.ru/data/2010/11/16/1214796647/10_02_06.pdf МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Дальневосточный федеральный университет» (ДВФУ)  филиал двфу в г. спасске-дальнем | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 0, предприятие не является банкротом,
0, предприятие не является банкротом,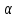 , %
, % х2
х2