|
|
ЕН.Ф.4 Эконометрика. Лекции 17 (час.) практические занятия 17 час семинарские занятия час лабораторные работы час
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака y характеризует коэффициент (индекс) детерминации 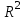 : :
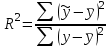 . .
Вопросы для самопроверки:
Модель парной линейной регрессии. Экономическая интерпретация.
Опишите метод наименьших квадратов.
Перечислите свойства линейного коэффициента корреляции.
Дайте графическую интерпретацию линейного коэффициента корреляции.
Назовите показатели качества регрессии.
Опишите нелинейные регрессионные модели: степенную, показательную, гиперболическую, параболическую.
Опишите процесс линеаризации нелинейных моделей.
Как осуществляется выбор лучшей модели.
Тема 3. Гетероскедастичность и автокорреляция
Учебные вопросы:
Последствия для свойств МНК-оценки. Вывод альтернативной оценки.
Гетероскедастичность и ее последствия.
Тесты на гетероскедастичность.
Устранение гетероскедастичности. Взвешенный метод наименьших квадратов.
Автокорреляция первого порядка. Тестирование на наличие автокорреляции.
Неправильная спецификация модели.
Медицина делится на анатомию, физиологию и патологию, первая изучает структуру организма, вторая – принципы действия, а патология – нарушения функционирования организма. Аналогично медицине рассмотрим «патологии» или недостатки регрессионного анализа, основанного на методе наименьших квадратов. К такому недостатку относится гетероскедастичность.
В силу воздействия неучтенных случайных факторов и причин отдельные наблюдения y будут в большей или меньшей степени отклоняться от функции регрессии f(x). В этом случае в общем виде уравнение взаимосвязи двух переменных может быть представлено в виде: 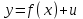 , где u – случайная переменная, характеризующая отклонение от функции регрессии. В случае парной линейной зависимости модель имеет вид: , где u – случайная переменная, характеризующая отклонение от функции регрессии. В случае парной линейной зависимости модель имеет вид: 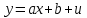 . .
Гомоскедастичность – условие «одинакового разброса», т.е. вероятность того, что величина u примет какое-то положительное (отрицательное) данное значение, будет одинаковой для всех наблюдений, т.е. 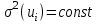 , , 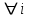 . .
Гетероскедастичность – условие «неодинакового разброса», 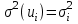 - дисперсия не обязательно одинакова для всех наблюдений i. - дисперсия не обязательно одинакова для всех наблюдений i.
Различают следующие виды гетероскедастичности:
1. СКО остатков растет по мере увеличения x. Поле корреляции такой гетероскедастичной модели представлено ниже:
2
. СКО остатков достигает максимальной величины при средних значениях переменной x и уменьшается при минимальных и максимальных значениях x.
3. Максимальное СКО остатков при малых значениях x и СКО остатков однородно по мере увеличения x.
Вариация y при больших значениях х гораздо больше, чем при малых значениях х. Зависимость y от x может вполне пригодиться для практических приложений, но результаты, связанные с анализом точности модели, оценкой значимости и построением доверительных интервалов, могут оказаться непригодными. Например, при небольших выборках есть риск получить оценку параметров, существенно отличающуюся от истинного параметра.
Очень часто проявление проблемы гетероскедастичности можно предвидеть заранее, основываясь на знании характера статистических данных. В таких случаях можно предпринять соответствующие действия по устранению этого эффекта еще на этапе спецификации модели, т.е. на этапе формулировки вида модели.
Рассмотрим два теста, в которых делаются различные предположения о зависимости между средним квадратическим отклонением случайного члена и величиной объясняющей переменной.
Тест ранговой корреляции Спирмена. При выполнении теста Спирмена предполагается, что среднее квадратическое отклонение случайной переменной либо увеличивается, либо уменьшается по мере увеличения x.
Этапы проведения теста:
Ранжируются значения x. Ранг – порядковый номер значения x. Ранжирование – упорядочивание. Если значения совпадают, то им присваивается ранг, равный среднему арифметическому из суммы мест, которые они занимают.
Вычисляются отклонения фактических значений от расчетных (остатки). Ранжируются остатки.
Вычисляется коэффициент ранговой корреляции по формуле 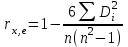 , где , где 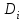 - разность между рангом x и рангом остатков. - разность между рангом x и рангом остатков.
Вычисляется t-статистика 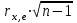 . Определяется по таблицам критерия Стьюдента при уровне значимости . Определяется по таблицам критерия Стьюдента при уровне значимости 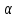 табличное значение при бесконечном числе степеней свободы. табличное значение при бесконечном числе степеней свободы.
По этому критерию гипотеза об отсутствии гетероскедастичности будет отклонена при уровне значимости 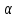 , если тестовая статистика , если тестовая статистика 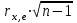 превышает табличное значение. (В примере тестовая статистика меньше табличного). превышает табличное значение. (В примере тестовая статистика меньше табличного).
Тест Голдфелда-Квандта. При проведении проверки по этому критерию, предполагается, что стандартное отклонение 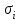 распределения вероятностей случайного члена распределения вероятностей случайного члена 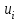 пропорционально значению пропорционально значению 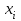 в этом наблюдении. Предполагается, что случайный член распределен нормально и не подвержен автокорреляции. в этом наблюдении. Предполагается, что случайный член распределен нормально и не подвержен автокорреляции.
Все n наблюдений упорядочиваются по x. Оцениваются отдельные регрессии для первых 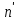 и последних и последних 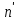 наблюдений, а средние наблюдений, а средние 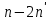 наблюдений отбрасываются. Если предположение о природе гетероскедастичности верно, то дисперсия случайного члена в последних наблюдений отбрасываются. Если предположение о природе гетероскедастичности верно, то дисперсия случайного члена в последних 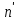 наблюдениях будут больше, чем в первых наблюдениях будут больше, чем в первых 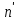 . Обозначая сумму квадратов остатков через . Обозначая сумму квадратов остатков через 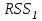 и и 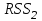 , рассмотрим их отношение , рассмотрим их отношение 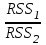 . Эта величина имеет F-распределение с . Эта величина имеет F-распределение с 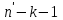 и и 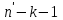 степенями свободы, где степенями свободы, где 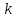 – число объясняющих переменных в регрессионном уравнении. – число объясняющих переменных в регрессионном уравнении.
Что же можно предпринять в отношении гетероскедастичности?
Пусть 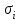 - среднее квадратическое отклонение случайной компоненты в i наблюдении. В том случае если бы было известно - среднее квадратическое отклонение случайной компоненты в i наблюдении. В том случае если бы было известно 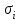 для каждого наблюдения, можно было бы устранить гетероскедастичность, разделив каждое наблюдение на соответствующее ему значение для каждого наблюдения, можно было бы устранить гетероскедастичность, разделив каждое наблюдение на соответствующее ему значение 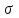 .Тогда случайный член в i-м наблюдении становится равным .Тогда случайный член в i-м наблюдении становится равным 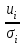 , и его теоретическая дисперсия представляется в виде: , и его теоретическая дисперсия представляется в виде: 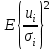 , что равняется: , что равняется: 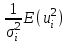 . Это выражение переписывается как . Это выражение переписывается как 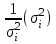 и, следовательно, оно равно единице. Таким образом, каждое наблюдение будет иметь случайный член, полученный из генеральной совокупности с единичной дисперсией, и модель будет гомоскедастичной. Теперь модель имеет вид: и, следовательно, оно равно единице. Таким образом, каждое наблюдение будет иметь случайный член, полученный из генеральной совокупности с единичной дисперсией, и модель будет гомоскедастичной. Теперь модель имеет вид: 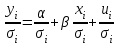 , что может быть переписано как , что может быть переписано как 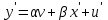 , где , где 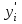 определяется как определяется как 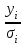 ; ; 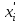 представляет собой представляет собой 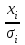 ; v — новая переменная,i-e наблюдение которой равно ; v — новая переменная,i-e наблюдение которой равно 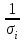 ; величина ; величина 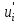 есть есть 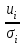 . Следует отметить, что в данном уравнении не должно быть постоянного члена. Оценивая регрессионную зависимость у' от v и х', мы получим эффективные оценки с несмещенными стандартными ошибками. . Следует отметить, что в данном уравнении не должно быть постоянного члена. Оценивая регрессионную зависимость у' от v и х', мы получим эффективные оценки с несмещенными стандартными ошибками.
Наблюдения с наименьшими значениями будут наиболее полезными для определения истинной зависимости между у и х, поскольку величина случайной переменной в них, как правило, наименьшая. Мы воспользуемся этим, оценивая так называемую взвешенную регрессию, придавая наибольшие веса наблюдениям самого «высокого качества», а наименьшие веса — соответственно, наблюдениям самого «низкого качества». Уравнение можно рассматривать как «взвешенный» вариант уравнения. После деления на z уравнение принимает вид: 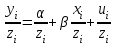 . Дисперсия случайного члена представлена как . Дисперсия случайного члена представлена как 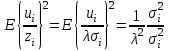 , что равно l/λ2. Следовательно, эта величина постоянна для всех наблюдений, и проблема устранена. , что равно l/λ2. Следовательно, эта величина постоянна для всех наблюдений, и проблема устранена.
Вопросы для самопроверки:
Что означает гетероскедастичность и каковы ее последствия.
Тесты на гетероскедастичность.
Объясните спроса на рабочую силу в терминах гетероскедастичности.
Устранение гетероскедастичности. Взвешенный метод наименьших квадратов.
Автокорреляция первого порядка. Тестирование на наличие автокорреляции.
Тема 4. Множественная линейная и нелинейная регрессия
и корреляция
Учебные вопросы:
Вывод и интерпретация коэффициентов множественной регрессии.
Индекс множественной корреляции. Индекс множественной детерминации.
Мультиколлинеарность. Отбор наиболее существенных факторных признаков в уравнении регрессии.
Множественная регрессия в нелинейных моделях. Типы нелинейных моделей.
Производственные функции. Моделирование производственной функции Кобба-Дугласа, связывающей объем выпуска с капитальными вложениями и затратами труда.
Линеаризация моделей.
Оценка коэффициентов уравнения регрессии и тесноты связи в ППП MS Excel. Инструменты анализа данных «Регрессия», «Корреляция».
Изучение связи между тремя и более связанными между собой признаками носит название множественной регрессии. При исследовании зависимостей методами множественной регрессии задача формулируется так же, как и при использовании парной регрессии: требуется определить аналитическое выражение связи между признаком у и объясняющими переменными 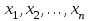 в виде в виде  . .
Построение модели множественной регрессии включает этапы:
Выбор формы связи.
Отбор факторных признаков.
Обеспечение достаточного объема совокупности для получения несмещенных оценок.
Множественный линейный регрессионный анализ является развитием парного регрессивного анализа применительно к случаям, когда зависимая переменная гипотетически связана с более чем одной независимой переменной зависимостью:
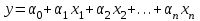
Как в случае парной регрессии, требуется выбрать такие значения коэффициентов 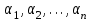 , чтобы обеспечить наилучшее соответствие. Оценка оптимальности соответствия определяется минимизацией суммы квадратов отклонений: , чтобы обеспечить наилучшее соответствие. Оценка оптимальности соответствия определяется минимизацией суммы квадратов отклонений:
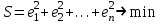 , ,
где 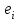 - остаток в i наблюдении, т.е. разница между фактическим значением y в этом наблюдении и значением - остаток в i наблюдении, т.е. разница между фактическим значением y в этом наблюдении и значением 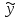 , прогнозируемом по уравнению регрессии. Рассмотрим случай двух объясняющих переменных: , прогнозируемом по уравнению регрессии. Рассмотрим случай двух объясняющих переменных: 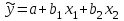 . Тогда остатки в этом случае будут равны . Тогда остатки в этом случае будут равны 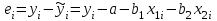 . Сумма квадратов остатков . Сумма квадратов остатков 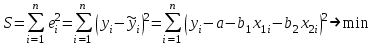 . Необходимые условия первого порядка для минимума имеют следующий вид: . Необходимые условия первого порядка для минимума имеют следующий вид:
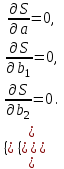
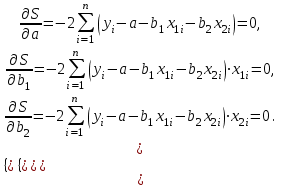
Таким образом, получим систему трех уравнений с тремя неизвестными 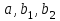 : :
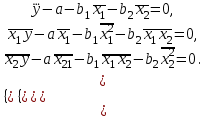
Вычисляя средние 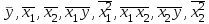 и решая систему уравнений, находим оценки a, b, c. и решая систему уравнений, находим оценки a, b, c.
В общем виде для линейных и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии:
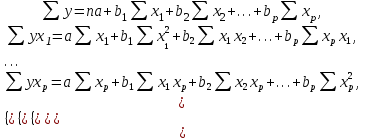
Для решения этой системы может быть применен метод Крамера, метод Гаусса, метод матричного исчисления, либо другой метод решения систем уравнений порядка n.
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:
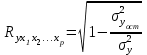 . .
Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:
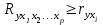 , , 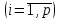 . .
Качество построенной модели в целом оценивает коэффициент (индекс) детерминации. Коэффициент множественной детерминации рассчитывается как квадрат индекса множественной корреляции:  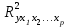 . .
Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле: 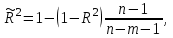 где n – число наблюдений, m – число факторов. где n – число наблюдений, m – число факторов.
При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов, их тесной линейной зависимости. Мультиколлинеарность – понятие, которое используется для описания проблемы, когда не строгая линейная зависимость приводит к получению ненадежных оценок регрессии. В этом случае можно предложить основные методы для смягчения мультиколлинеарности: в случае временных рядов следует сократить продолжительность каждого периода времени, можно увеличить точность оценок и ослабить проблему мультиколлинеарности за счет большого расхода средств на увеличение размера выборки, возможность введения новой переменной в уравнение регрессии 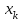 , оказывающей влияние на u. Однако, если эта переменная связана с некоторой переменной, уже находящейся в уравнении регрессии, то это только усугубит проблему мультиколлинеарности. , оказывающей влияние на u. Однако, если эта переменная связана с некоторой переменной, уже находящейся в уравнении регрессии, то это только усугубит проблему мультиколлинеарности.
Если имеется возможность собрать данные, то нужно постараться сделать так, чтобы получить выборку, в которой независимые переменные слабо связаны между собой.
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы 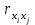 , , 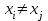 были бы равны нулю. Так, для включающего три объясняющих переменных уравнения были бы равны нулю. Так, для включающего три объясняющих переменных уравнения
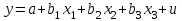
матрица коэффициентов корреляции между факторами имела бы определитель, равный 1:
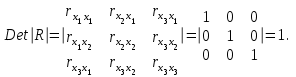
Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0:
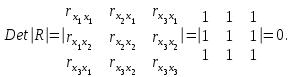
Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Проверка мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных 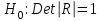 . Доказано, что величина . Доказано, что величина 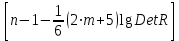 имеет приближенное распределение x2 с имеет приближенное распределение x2 с 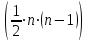 степенями свободы. Если фактическое значение x2 превосходит табличное (критическое) степенями свободы. Если фактическое значение x2 превосходит табличное (критическое) 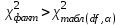 , то гипотеза H0 отклоняется. Это означает, что , то гипотеза H0 отклоняется. Это означает, что 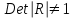 , недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной. , недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.
Практика построения множественных регрессионных моделей взаимосвязи показывает, что реально существующие взаимосвязи между социально-экономическими явлениями можно описать пятью типами моделей:
Линейная: 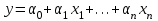 . .
Степенная: 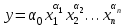 . .
Показательная: 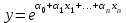 . .
Параболическая: 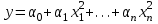 . .
Гиперболическая: 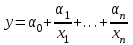 . .
Примером множественной функции регрессии является производственная функция Кобба-Дугласа: 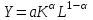 , показывающая зависимость реального объема выпуска от капитальных затрат и затрат труда. , показывающая зависимость реального объема выпуска от капитальных затрат и затрат труда.
Применим линейный регрессионный анализ для нахождения параметров производственной функции Кобба –Дугласа 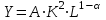 , где K - затраты капитала, L - объем трудовых затрат. Обозначим , где K - затраты капитала, L - объем трудовых затрат. Обозначим 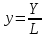 - индекс производительности труда, - индекс производительности труда, 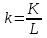 - индекс фондовооруженности и поделив равенство - индекс фондовооруженности и поделив равенство 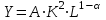 на L получим: на L получим: 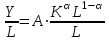  или или 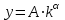 . Прологарифмируем обе части последнего равенства . Прологарифмируем обе части последнего равенства 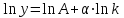 Используя метод наименьших квадратов получим систему уравнений для Используя метод наименьших квадратов получим систему уравнений для 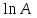 и и 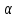 : :
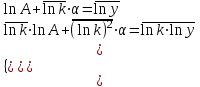 , ,
где 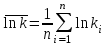 , , 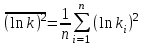 , , 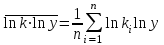 . .
Вопросы для самопроверки:
Вывод и интерпретация коэффициентов множественной регрессии.
Показатели тесноты связи во множественной регрессии.
Проблема мультиколлинеарности. Проблема отбора наиболее существенных факторных признаков в уравнении регрессии.
Применение линейных множественных регрессий в ценообразовании.
Типы нелинейных множественных регрессий.
Построение производственной функции Кобба-Дугласа, связывающей объем выпуска с капитальными вложениями и затратами труда.
Оценка коэффициентов уравнения регрессии и тесноты связи в ППП MS Excel. Инструменты анализа данных «Регрессия», «Корреляция».
|
|
|
 Скачать 1.23 Mb.
Скачать 1.23 Mb.
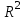 :
: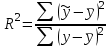 .
.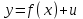 , где u – случайная переменная, характеризующая отклонение от функции регрессии. В случае парной линейной зависимости модель имеет вид:
, где u – случайная переменная, характеризующая отклонение от функции регрессии. В случае парной линейной зависимости модель имеет вид: 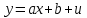 .
.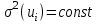 ,
, 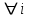 .
.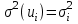 - дисперсия не обязательно одинакова для всех наблюдений i.
- дисперсия не обязательно одинакова для всех наблюдений i.
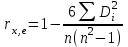 , где
, где 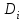 - разность между рангом x и рангом остатков.
- разность между рангом x и рангом остатков. 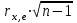 . Определяется по таблицам критерия Стьюдента при уровне значимости
. Определяется по таблицам критерия Стьюдента при уровне значимости 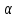 табличное значение при бесконечном числе степеней свободы.
табличное значение при бесконечном числе степеней свободы.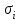 распределения вероятностей случайного члена
распределения вероятностей случайного члена 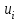 пропорционально значению
пропорционально значению 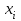 в этом наблюдении. Предполагается, что случайный член распределен нормально и не подвержен автокорреляции.
в этом наблюдении. Предполагается, что случайный член распределен нормально и не подвержен автокорреляции.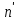 и последних
и последних 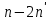 наблюдений отбрасываются. Если предположение о природе гетероскедастичности верно, то дисперсия случайного члена в последних
наблюдений отбрасываются. Если предположение о природе гетероскедастичности верно, то дисперсия случайного члена в последних 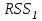 и
и 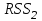 , рассмотрим их отношение
, рассмотрим их отношение 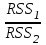 . Эта величина имеет F-распределение с
. Эта величина имеет F-распределение с 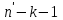 и
и 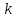 – число объясняющих переменных в регрессионном уравнении.
– число объясняющих переменных в регрессионном уравнении.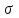 .Тогда случайный член в i-м наблюдении становится равным
.Тогда случайный член в i-м наблюдении становится равным 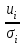 , и его теоретическая дисперсия представляется в виде:
, и его теоретическая дисперсия представляется в виде: 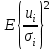 , что равняется:
, что равняется: 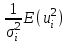 . Это выражение переписывается как
. Это выражение переписывается как 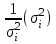 и, следовательно, оно равно единице. Таким образом, каждое наблюдение будет иметь случайный член, полученный из генеральной совокупности с единичной дисперсией, и модель будет гомоскедастичной. Теперь модель имеет вид:
и, следовательно, оно равно единице. Таким образом, каждое наблюдение будет иметь случайный член, полученный из генеральной совокупности с единичной дисперсией, и модель будет гомоскедастичной. Теперь модель имеет вид: 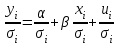 , что может быть переписано как
, что может быть переписано как 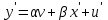 , где
, где 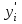 определяется как
определяется как 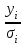 ;
; 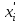 представляет собой
представляет собой 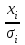 ; v — новая переменная,i-e наблюдение которой равно
; v — новая переменная,i-e наблюдение которой равно 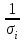 ; величина
; величина 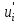 есть
есть 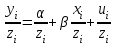 . Дисперсия случайного члена представлена как
. Дисперсия случайного члена представлена как 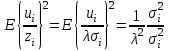 , что равно l/λ2. Следовательно, эта величина постоянна для всех наблюдений, и проблема устранена.
, что равно l/λ2. Следовательно, эта величина постоянна для всех наблюдений, и проблема устранена.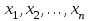 в виде
в виде  .
. 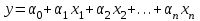
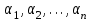 , чтобы обеспечить наилучшее соответствие. Оценка оптимальности соответствия определяется минимизацией суммы квадратов отклонений:
, чтобы обеспечить наилучшее соответствие. Оценка оптимальности соответствия определяется минимизацией суммы квадратов отклонений: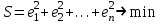 ,
,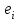 - остаток в i наблюдении, т.е. разница между фактическим значением y в этом наблюдении и значением
- остаток в i наблюдении, т.е. разница между фактическим значением y в этом наблюдении и значением 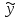 , прогнозируемом по уравнению регрессии. Рассмотрим случай двух объясняющих переменных:
, прогнозируемом по уравнению регрессии. Рассмотрим случай двух объясняющих переменных: 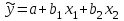 . Тогда остатки в этом случае будут равны
. Тогда остатки в этом случае будут равны 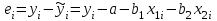 . Сумма квадратов остатков
. Сумма квадратов остатков 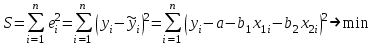 . Необходимые условия первого порядка для минимума имеют следующий вид:
. Необходимые условия первого порядка для минимума имеют следующий вид: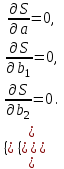
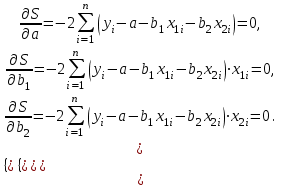
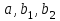 :
: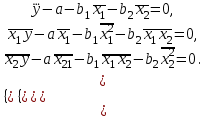
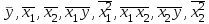 и решая систему уравнений, находим оценки a, b, c.
и решая систему уравнений, находим оценки a, b, c.
 .
.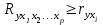 ,
, 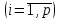 .
.
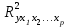 .
.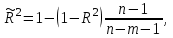 где n – число наблюдений, m – число факторов.
где n – число наблюдений, m – число факторов.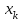 , оказывающей влияние на u. Однако, если эта переменная связана с некоторой переменной, уже находящейся в уравнении регрессии, то это только усугубит проблему мультиколлинеарности.
, оказывающей влияние на u. Однако, если эта переменная связана с некоторой переменной, уже находящейся в уравнении регрессии, то это только усугубит проблему мультиколлинеарности.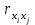 ,
, 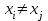 были бы равны нулю. Так, для включающего три объясняющих переменных уравнения
были бы равны нулю. Так, для включающего три объясняющих переменных уравнения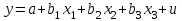
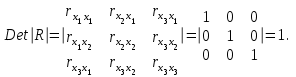
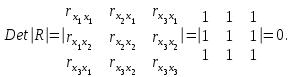
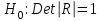 . Доказано, что величина
. Доказано, что величина 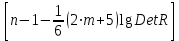 имеет приближенное распределение x2 с
имеет приближенное распределение x2 с 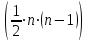 степенями свободы. Если фактическое значение x2 превосходит табличное (критическое)
степенями свободы. Если фактическое значение x2 превосходит табличное (критическое) 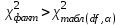 , то гипотеза H0 отклоняется. Это означает, что
, то гипотеза H0 отклоняется. Это означает, что 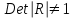 , недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.
, недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.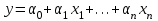 .
.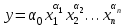 .
.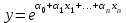 .
.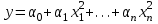 .
. 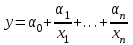 .
. 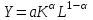 , показывающая зависимость реального объема выпуска от капитальных затрат и затрат труда.
, показывающая зависимость реального объема выпуска от капитальных затрат и затрат труда.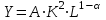 , где K - затраты капитала, L - объем трудовых затрат. Обозначим
, где K - затраты капитала, L - объем трудовых затрат. Обозначим 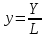 - индекс производительности труда,
- индекс производительности труда, 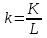 - индекс фондовооруженности и поделив равенство
- индекс фондовооруженности и поделив равенство 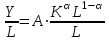
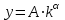 . Прологарифмируем обе части последнего равенства
. Прологарифмируем обе части последнего равенства 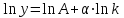 Используя метод наименьших квадратов получим систему уравнений для
Используя метод наименьших квадратов получим систему уравнений для 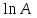 и
и  ,
,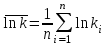 ,
, 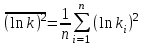 ,
, 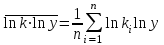 .
.