лекции. Лекции Общая электротехника. Лекции по дисциплине Общая электротехника для студентов специальностей

• Название: Лекции по дисциплине Общая электротехника для студентов специальностей
• Анкор: лекции
• Дата: 17.04.2022
• Размер: 4.27 Mb.
• Имя файла: Лекции Общая электротехника.docx
• Тип: Лекции; #480717
• страница: 1 из 11

Р ОСЖЕЛДОР

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Ростовский государственный университет путей сообщения»

(ФГБОУ ВО РГУПС)

Филиал РГУПС в г. Минеральные Воды
В.Я. Яловой
Лекции

по дисциплине

Общая электротехника
для студентов специальностей

23.05.03 Подвижной состав железных дорог

Минеральные Воды

2017 г.

В.Я. Яловой

Лекции по дисциплине «Электроника и электротехника». /Яловой В.Я.. – Минеральные Воды: Филиал ФГБОУ ВО РГУПС в г. Минеральные Воды, 2017. – 134 с.
Лекции предназначены для студентов очного и заочного обучения специальностей 23.05.03 Подвижной состав железных дорог,

Лекции включают теоретический материал и рекомендованы к использованию в учебном процессе кафедрой «Естественнонаучных и инженерных дисциплин».

Яловой В.Я..

 Филиал Ростовского государственного университета

путей сообщения в г. Минеральные Воды, 2017
Раздел 1. Электрические цепи постоянного тока

Лекция 1. Основные понятия, определения, законы электрических цепей

1) Структура электрической цепи.

Электрической цепью называется совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электродвижущей силе, токе и напряжении.

В электрической цепи постоянного тока могут действовать как постоянные токи, т. е. такие, значение и направление которых в любой момент времени остаются неизменными, так и токи, направление которых остается постоянным, а значение изменяется во времени произвольно или по какому-либо закону (такие токи нельзя назвать строго постоянными).

Под цепями постоянного тока в современной технике подразумевают цепи, в которых ток не меняет своего направления, т. е. полярность источников э. д. с. в которых постоянна.

Электрическая цепь состоит из отдельных устройств или элементов, которые по назначению можно подразделить на три группы.

1. Элементы, предназначенные для генерирования (выработки) электроэнергии (источники питания или источники э. д. с.).

2. Элементы, преобразующие электроэнергию в другие виды энергии (механическую, тепловую, световую, химическую и т. д.); эти элементы называются приемниками электрической энергии или нагрузкой.

3. Элементы, предназначенные для передачи электроэнергии от источника питания к электроприемнику (провода, устройства, обеспечивающие уровень и качество напряжения, и др.).

Электрическая цепь, электрическое сопротивление участков которой не зависит от значений и направлений токов и напряжений в цепи, называется линейной электрической цепью. Такая цепь состоит только из линейных элементов, а ее состояние описывается линейными алгебраическими уравнениями. В противном случае цепь называется нелинейной и описывается более сложными математическими уравнениями.

2) Схемы замещения.

Для расчета и анализа работы электрической цепи, состоящей из любого количества различных элементов, удобно эту цепь представить графически (рис. 1). Графическое изображение электрической цепи, содержащее условные обозначения ее элементов и показывающее соединения этих элементов, называется схемой электрической цепи. Простейшая схема электрической цепи, состоящая из источника э. д. с. (Е) и резистора с сопротивлением (R), изображена на рис. 1а).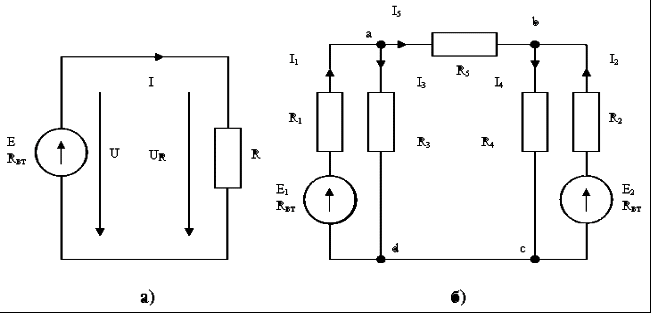



Рис. 2.1. Схемы электрических цепей: а) простейшей одноконтурной, б) многоконтурной (p=5, q=3)

Участок электрической цепи, вдоль которого протекает один и тот же ток, называется ветвью. Место соединения ветвей электрической цепи называется узлом.

На электрических схемах узел обозначают точкой (рис.1б)). Иногда несколько геометрических точек, соединенных проводниками, сопротивление которых принимают равным нулю (c иd), образуют один узел (рис. 1б), узел с. Таким образом, каждая ветвь соединяет два соседних узла электрической схемы. Число ветвей схемы принято обозначать р, а число узлов q. Электрическая цепь, изображенная на схеме рис. 1.б), имеет число ветвей р = 5 и число узлов q = 3 (а, b, с).

Любой замкнутый путь, проходящий по нескольким ветвям, называют контуром электрической цепи. Простейшая электрическая цепь имеет одноконтурную схему (см. рис. 1, а), сложные электрические цепи - несколько контуров (рис. 1, б).

3) Идеальные источники питания.

Источники электрической энергии являются необходимым элементом любой электрической цепи.Их разделяют на идеальные и реальные источники. В свою очередь, идеальные источники делятся на источники электродвижущей силы (ЭДС) и источники тока .

Источники ЭДС- это такие элементы электрической цепи, у которых разность потенциалов на выходе не зависит от величины и направления протекания тока, т.е. их вольтамперные характеристики (ВАХ) представляют собой прямые линии параллельные оси I.

Направление стрелки в условном обозначении источника ЭДС указывает направление действия ЭДС, поэтому направление падения напряжения на выходных зажимах источника всегда противоположно.Так как на ВАХ электрическое сопротивление соответствует котангенсу угла наклона характеристики, то сопротивление источника ЭДС равно нулю, а проводимость, соответственно, бесконечности.

Источники тока - это такие элементы электрической цепи, у которых протекающий через них ток не зависит от знака и значения разности потенциалов на выходе, т.е. их (ВАХ) представляют собой прямые линии параллельные оси U. Отсюда, сопротивление источника тока равно бесконечности, а проводимость - нулю.

Направление стрелки в условном обозначении источника тока указывает направление протекания тока.

Источники ЭДС и источники тока часто рассматриваются как некие абстракции, не имеющие реального физического воплощения. Однако, это справедливо только, если считать, что их ВАХ не имеют ограничения. В этом случае ток через источник ЭДС или падение напряжения на источнике тока могут достигать бесконечно больших значений. При этом мощность источника (P=U*I) должна быть бесконечно большой, что исключает возможность технической реализации.

Если же ток и/или напряжение источника ограничено, то свойствами идеального источника обладают, например, стабилизированные источники питания,типичная ВАХкоторых приведена на рис. 1

Выходное напряжение такого устройства U_вых постоянно до тех пор, пока ток нагрузки не достигнет максимально допустимого значения I_max, после чего источник питания из режима стабилизации напряжения переходит в режим стабилизации т 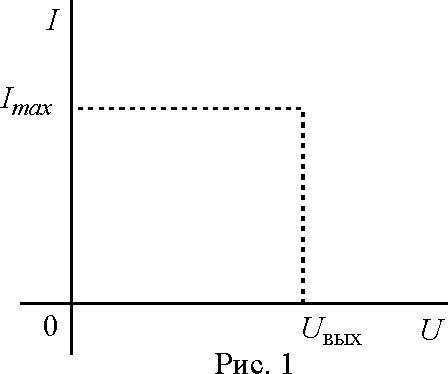ока.

ВАХидеального источника ЭДС и источника тока.
В пределах обоих режимов источник питания обладает свойствами соответственно идеального источника ЭДС и источника тока.

Идеальные источники ЭДС и тока используются также для моделирования некоторых электромагнитных процессов и нелинейных элементов электрических цепей, таких, например, как диод.

4) Режимы работы цепи

Для электрической цепи наиболее характерными являются ре­жимы работы: нагрузочный, холостого хода и короткого замыкания.

Нагрузочный режим работы - работа электри­ческой цепи при подключении к источнику какого-либо приемника с сопротивлением R (резистора, электрической лампы и т. п.).

Режим холостого хода-при этом режиме присоединенная к источнику электрическая цепь разомкнута, т. е. тока в цепи нет. Таким образом, в режиме холостого хода напряжение на зажимах источника электрической энергии равно его эдс. Это обстоятельство можно использовать для измерения эдс источников электроэнергии.

Режим короткого замыкания. Коротким замыканием (к з) называют такой режим работы источника, когда его зажимы замкнуты проводником, сопротивление которого можно считать равным нулю. Практически кз возникает при соединении друг с другом проводов, связывающих источник с приемником, так как эти провода имеют обычно незначительное сопротивление и его можно принять равным нулю. Кз может происходить в результате неправильных действий персонала, обслуживающего электротехнические установки или при повреждении изоляции проводов.

Лекция 2. Законы Ома и Кирхгофа
1) Законы Ома и Кирхгофа для цепей постоянного тока.

Закон ома

Ток на участке электрической цепи прямо пропорционален напряжению на этом участке и обратно пропорционален его сопротивлению.

I = UR/R, I = E/(R + Rвт). (1)

Законы Кирхгофа

Соотношения между токами и э. д. с. в ветвях электрической цепи и напряжениями на элементах цепи, позволяющие произвести расчет электрической цепи, определяются двумя законами Кирхгофа.

Первый закон Кирхгофа отражает принцип непрерывности движения электрических зарядов, из которого следует, что все заряды, притекающие в любой узел электрической цепи, из него вытекают, т. е. не накапливаются в узле. Поэтому алгебраическая сумма токов в ветвях, сходящихся в узле электрической цепи, равна нулю, т. е.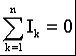

(2)

где n - число ветвей, сходящихся в узле.

До написания уравнения (2) необходимо задать условные положительные направления токов в ветвях, обозначив эти направления на схеме стрелками. В уравнении (2) токи, направленные к узлу, записывают с одним знаком (например, с плюсом), а токи, направленные от узла, с противоположным (с минусом). Таким образом, для узла b схемы (рис. 1) уравнение по первому закону Кирхгофа будет иметь вид: I_1- I₂ +I₃-I₄ = 0.

Первый закон Кирхгофа может быть сформулирован иначе: сумма токов, притекающих в узел, равна сумме токов, вытекающих из узла.

Тогда уравнение для узла b (рис. 1) будет записано так:

I₁-I₂=I₆.

Второй закон Кирхгофа определяет, что изменение потенциала во всех элементахконтура в сумме равно нулю. Это значит, что при обходе контура abcda электрической цепи, показанной на рис. 1, в силу того, что потенциал точки а один и тот же, общее изменение потенциала в контуре равно нулю. Из этого следует, что алгебраическая сумма э. д. с. в любом контуре электрической цепи постоянного тока равна алгебраической сумме падений напряжений на всех элементах, входящих в этот контур, т. е.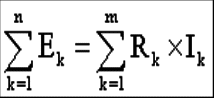

, (3)

где n- число источников э. д. с. в контуре; m- число элементов (число ветвей) с сопротивлением R_k в контуре.



Рис. 1. Сложная одноконтурная электрическая цепь

При составлении уравнений по второму закону Кирхгофа предварительно задают условные положительные направления токов во всех ветвях электрической цепи и для каждого контура выбирают направление обхода. Если при этом направление э. д. с. совпадает с направлением обхода контура, то такую эдс берут сoзнаком плюс, если не совпадает - со знаком минус (левая часть уравнения 3). Падения напряжений в правой части уравнения (3) берут со знаком плюс, если положительное направление тока в данном элементе цепи совпадает с направлением обхода контура, и со знаком минус? если такого совпадения нет.

Для контура abcda, сопротивления ветвей которого включают в себя и внутренние сопротивления источников эдс, уравнение (3) принимает вид

E₁ - E₂+ E₃= R₁ I₁ - R₂ I₂+ R₃ I₃ - R₄ I₄.

Используя второй закон Кирхгофа, можно определять разность потенциалов (напряжение) между любыми двумя точками электрической цепи.

Следовательно, второй закон Кирхгофа можно cформулировать в таком виде: сумма падений напряжений на всех элементах контура, включая источники э. д. с., равна нулю, т. е.

. (4)

Если в ветви имеется n последовательно соединенных элементов с сопротивлением k-го элемента R_k, то

, (5)

т. е. падение напряжения на участке цепи или напряжение между зажимами ветви U, состоящей из последовательно соединенных элементов, равно сумме падений напряжений на этих элементах.
2) Виды соединений элементов цепи.

В простейшей электрической цепи генератор, электроприемник и связывающие их провода, по которым электрическая энергия передается от генератора к приемнику, соединены между собой последовательно. Этот способ соединения применяется для того, чтобы связать в общую электрическую систему разнохарактерные с энергетической точки зрения элементы цепи генераторы, электроприемники и линии передачи электрической энергии. Однородные в энергетическом отношении элементы системы, например генераторы или электроприемники, как правило, соединяются между собой параллельно. При таком способе соединения достигается относительная независимость в управлении и работе отдельных источников и потребителей электроэнергии. Между тем при последовательном соединении практически невозможно включать и отключать отдельно каждый генератор или электроприемник, а также устанавливать для любого из них требуемый режим, работы. Кроме того, при последовательном соединении приемников, например электрических ламп, перегорание одной из них влечет за собой погасание всех остальных.

Совместная параллельная работа генераторов на общую электрическую нагрузку имеет значительные преимущества в сравнении с раздельной работой каждого генератора на свою нагрузку. Во-первых, повышается надежность питания потребителей, так как в случае аварийного отключения одного из генераторов оставшиеся в работе генераторы могут обеспечить бесперебойное электроснабжение наиболее ответственных нагрузок. Во-вторых, при параллельной работе можно в случае снижения нагрузки (например, в ночное время или в выходные дни) отключать часть генераторов, что повышает экономичность эксплуатации энергетических установок.

В тех случаях, когда один источник (например, электрохимический аккумулятор с э.д.с. Е = 1,25—2,4 В) не обеспечивает требуемого напряжения (110 или 220 В), приходится применять последовательное соединение однотипных источников.



Рис. 2 Схема сложной цепи постоянного тока

Последовательное включение однотипных приемников (например, электрических ламп) применяется в исключительных случаях, когда напряжение источника значительно превышает номинальное напряжение отдельных электроприемников.
3) Определение эквивалентных сопротивлений. Методы расчета простых цепей.

Цепи с последовательным соединением. Если электрическая цепь состоит из нескольких последовательно соединенных участков с сопротивлениями r₁, r₂, r₃, r₄ (рис. 3), то через все участки протекает один и тот же ток I.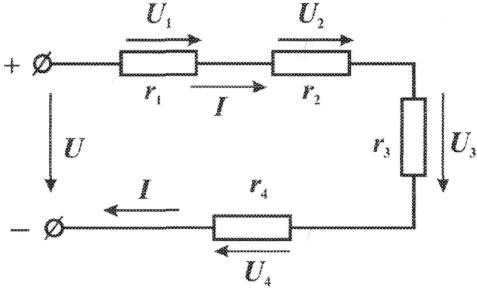



Рис. 3. Цепь с последовательным соединением сопротивлений

При отсутствии на участках цепи собственных эдс.¹ общее напряжение U, приложенное к зажимам всей цепи, равно сумме падений напряжения на отдельных элементах цепи (второй закон Кирхгофа):

U + U₁ + U₂ + U₃ + U₄ (6)

или

U = I r₁ + I r₂ + I r₃ + I r₄ = I (r₁ + r₂ + r₃ + r₄) (7)

Из этого выражения следует, что общее сопротивление r равно сумме сопротивлений всех последовательно соединенных элементов цепи, а напряжения между элементами распределяются прямо пропорционально их сопротивлениям.

Если уравнение (7) умножить на I, то получим

UI = I² r₁ + I² r₂ + I² r₃ + I² r₄ (8)

или

P = P₁ + P₂ + P₃ + P₄ (9)

т. е. общая мощность Р, потребляемая цепью, равна сумме мощностей, потребляемых отдельными ее элементами.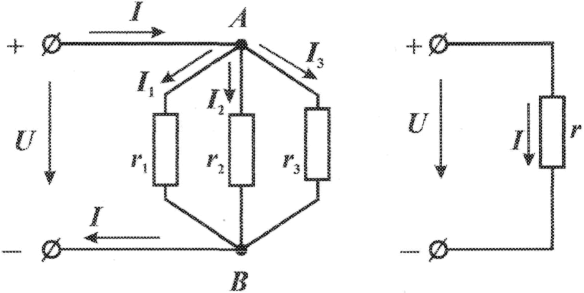



Рис. 4. Разветвленная цепь постоянного тока
Цепи с параллельным соединением. При параллельном соединении электроприемников (рис. 4) все они находятся под одинаковым напряжением U.

Обозначим сопротивления отдельных электроприемников через r₁, r₂, r₃, их проводимости - соответственно через g₁, g₂, g₃, а токи—через I₁, I₂, I₃.

Общий ток I в неразветвленной части цепи равен сумме токов, потребляемых отдельными электроприемниками: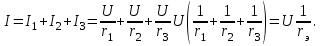

(10)

или

I = U g₁ + U g₂ + U g₃ = U (g₁ + g₂ + g₃) = U g_э (11)

Эквивалентная проводимость разветвленной цепи равна сумме проводимостей отдельных ее ветвей: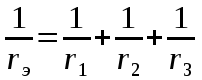

(12)

или

g = g₁ + g₂ + g₃ (12а)

В частном случае, когда цепь содержит два параллельно включенных сопротивления r₁ и r₂, эквивалентное сопротивление r_э удобно определять по формуле, вытекающей из выражения (12):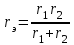

(13)

Умножив уравнения (10) на U, получим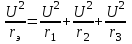

(14)

или

P₁ = P₁ + P₂ + P₃ (15)
Из изложенного следует что мощность, расходуемая в разветвленной цепи, равна сумме мощностей, потребляемых отдельными приемниками или одним эквивалентным приемником. Проводимость эквивалентного приемника равна сумме проводимостей всех параллельно включенных электроприемников. Токи в этих приемниках так же, как и мощности, распределяются всегда пропорционально проводимостям.

При включении нескольких генераторов для совместной параллельной работы (рис. 5) они соединяются между собой одноименными зажимами, а к общим узловым точкам присоединяется внешняя цепь (нагрузка).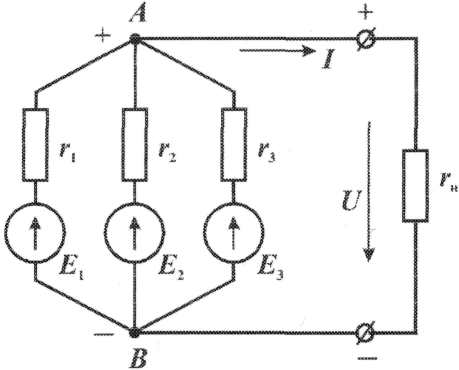



Рис. 5. Параллельна работа источника питания

При этом эдс всех генераторов будут иметь одинаковое направление относительно их общей нагрузки.

Цепи со смешанным соединений с одной эдс. Основная задача расчета электрических цепей — определить токи и мощности в различных элементах цепи (генераторах, электроприемниках и линиях, соединяющих источники энергии с потребителями), а также напряжения на отдельных элементах исследуемой цепи.

Исходными данными для расчета обычно являются заданные эдс, действующие в этой цепи, и характеристики (параметры) различных элементов цепи, т. е. либо их сопротивления, либо номинальные напряжения и мощности. При условии постоянства (по величине и направлению) действующих в цепи эдс и неизменности сопротивлений, образующих эту цепь, картина распределения напряжений, токов и мощностей в данной схеме может быть только одна, т. е. задача имеет однозначное решение.

Если электрическая цепь представляет собой сочетание последовательно и параллельно включенных сопротивлений (смешанная схема соединений) и при этом имеет один источник питания (одну эдс), то она рассчитывается в следующем порядке:

1) путем последовательного упрощения схемы находят общее сопротивление цепи;

2) по закону Ома определяют общий ток;

3) находят распределение токов и напряжений в схеме.

Лекция 3. Расчёт сложных цепей постоянного тока

1) Метод непосредственного применения законов Кирхгофа

Применение метода рассмотрим на примере схемы рис. 1,а. Метод основан на непосредственном приме­нении для расчета схемы уравнений по первому и второму законам Кирхгофа. Необходимое число уравнений равно числу неизвестных токов в ветвях. В данном случае неиз­вестных токов три, следовательно необходимо составить си­стему из трех уравнений. Для составления уравнений не­обходимо предварительно задаться направлением токов в ветвях. Так как эти токи пока неизвестны ни по величине, ни по направлению, принимаем направление этих токов про­извольно. В случае, если какие-либо токи ошибочно направ­лены не так, как они протекают, соответствующий резуль­тат получится с отрицательным знаком. При этом никаких новых расчетов не производится, а просто изменяют на­правление тока на правильное.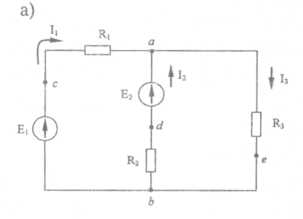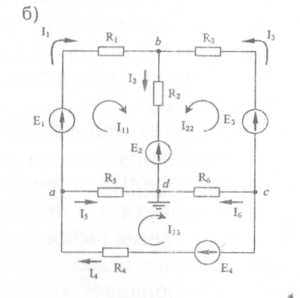



Рис. 1.

При составлении уравнений обычно вначале составля­ют наибольшее возможное число уравнений по первому за­кону Кирхгофа, т.к. эти уравнения более просты. Однако здесь надо следить за тем, чтобы эти уравнения были не­зависимы, т.е. не являлись следствием или повторением предыдущих, уже записанных уравнений. Например, в схе­ме (рис. 1,а) два узла, однако может быть записано только одно уравнение, в чем легко убедиться, записав уравнения для узлов а и Ь. В общем случае для схемы, имеющей пузлов, можно записать п-1 уравнений по первому закону Кирхгофа. Например, для схемы (рис. 1.б), имеющей четыре узла, может быть записано три уравнения по перво­му закону Кирхгофа. Недостающие уравнения записываем по второму закону Кирхгофа. При этом следует предварительно выбрать контуры, для которых будем составлять эти уравнения. Здесь также следует следить за тем, чтобы эти уравнения были независимы. Практически для этого дос­таточно, чтобы в каждое следующее уравнение входила хотя бы одна новая ветвь, не входившая в предыдущие. В схеме (рис. 1,а) можно выделить три замкнутых конту­ра: ndbca, bdaebи bcaeb,однако только два из уравнений для этих контуров будут независимыми. Составим, напри­мер, уравнения по второму закону Кирхгофа для контуров ndbcaи bdaeb.При составлении уравнений безразлично, обходить ли замкнутый контур по часовой стрелке или против, так как это приведет лишь к изменению всех зна­ком в уравнении на обратные. Тогда полная система урав­нений для расчета схемы рис.1.,а:

I₁ + I₂ - I₃ = 0;

I₁R₁-I₂R₂=E_l-E₂; (1)

I₂R₂+I₃R₃= Е₂.

В результате решения этой системы находим искомые токи I₁,I₂,I₃. Решение может быть выполнено любым известным методом.

Оценивая данный метод, отметим, что даже для такой простой схемы, как схема (рис.1,а) приходится решать систему из трех уравнений. Для более сложных схем задача резко усложняется. Например, для схемы (рис. 1,б) получим систему из шести уравнений. Поэтому областью при­менения метода уравнений Кирхгофа является расчет не очень сложных схем. При ручном счете без применения ЭВМ таким методом обычно рассчитывают схемы, описываемые системой не более, чем из трех уравнений.

2)Метод контурных токов.

При расчете сложных цепей с большим числом узловых точек предпочтителен метод контурных токов, который позволяет освободиться от составления уравнений по первому закону Кирхгофа и тем самым значительно сократить общее число совместно решаемых уравнений.

Сущность этого метода поясним на рис. 2, на котором представлена сложная цепь с узловыми точкамиА, В, С, D. Заданную схему разбиваем на три смежных контура /, //, /// с произвольно выбранными направлениями токов. Если считать, что в каждом из этих контуров протекает свой контурный ток (I_I, I_II, I_III), то в ветвях, являющихся общими для двух смежных контуров, протекающие токи равны алгебраической сумме двух контурных токов (в ветви АВ протечет ток I₂ = I_II - I_I, в ветви ВС - ток I₅ = I_I - I_III и в ветви DB - ток I₄ = I_II - I_III).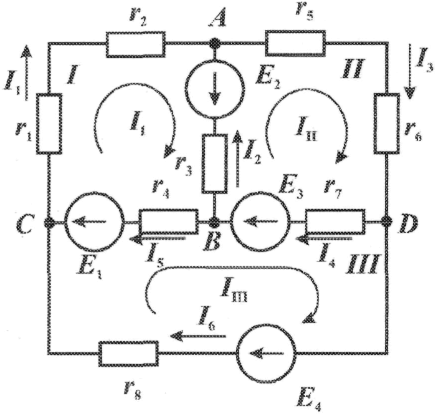



Рис. 2. Схема цепи к расчету методом контурных токов

Применяя к отдельным контурам второй закон Кирхгофа, получим систему с числом уравнений, равным числу контурных токов:

E₁ + E₂ = I₁ (r₁ + r₂) + (I_I – I_II) + (I_I – I_III) r₄

E₃ - E₂ = I_II (r₅ + r₆) + (I_II – I_III) r₇+ (I_II – I_I) r₃

E₄ – E₁ – E₃= I_III r₃ + (I_III – I_I) r₄+ (I_III – I_II) r₇

Эти уравнения можно представить в виде, более удобном для их совместного решения:

E ₁ + E₂ = I₁ (r₁ + r₂ + r₃ + r₄) – I_II r₃ – I_III r₄

E₃ - E₂ = I_II (r₅ + r₆ + r₇ + r₃) – I_I r₃ – I_III – r₇ (2)

E₄ – E₁ – E₃= I_III (r₄ + r₇ + r₈) - I_Ir₄ – I_II r₇
Определив контурные токи I_I, I_II, I_III, нетрудно найти токи в смежных ветвях АВ, ВС и DB.

3) Метод узловых потенциалов

В основе этого метода также лежит принцип замены переменных. Здесь вместо искомых токов в ветвях будем определять потенциалы узловых точек схемы. Зная их, мож­но, используя потенциальные соотношения, по второму закону Кирхгофа, найти токи в ветвях.

Предварительно отметим, что любую точку электричес­кий схемы можно заземлить, если ранее ни одна другая точ­ка с другим потенциалом не была

заземлена. Заземление какой-либо точки схемы свидетельствует лишь о том, что потенциал этой точки принят равным нулю. Распределение токов в схеме при этом не изменится, так как не возникает никаких новых ветвей и цепей для протекания тока. Нельзя, однако, заземлять одновременно две или более точек, если они имеют разные потенциалы, так как в этом случае обра­зуются дополнительные ветви, и схема, в сущности, стано­вится другой.

Воспользовавшись приведенными соображениями, заземлим, например, узловую точку dсхемы (рис. 1,б). Тем самым потенциал этой точки стал известен (равен нулю). Следовательно для расчета этой схемы методом узловых потенциалов достаточно определить только потенциалы ос­тальных узлов а,b,с. Практически в сложных схемах выгод­нее заземлять тот узел, где сходится больше всего ветвей. Составим для узлов а,b,с уравнения по первому закону Кирхгофа: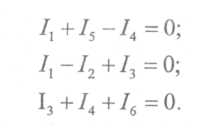



(3)

Выразим все токи схемы через потенциалы узловых точек, учитывая, что φ_d = 0: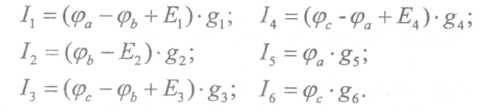

(4)

Подставив 1₁, 1_5, 1₄ в полученное выражение для токов в уравнении (4) по первому закону Кирхгофа для узла а, получим после группировки слагаемых:

(5)

Введем следующие обозначения: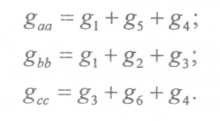



(6)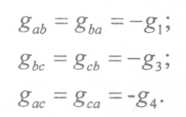

Эти величины представляют собой арифметическую сумму проводимостей ветвей, примыкающих к соответству­ющему узлу схемы. Далее обозначим:
(7)

Эти величины представляют собой проводимость вет­вей, соединяющих соответствующие узлы, взятые со зна­ком минус. Если между какой-либо парой узлов ветвь схе­мы соответствует, соответствующая проводимость равна нулю. И, наконец, обозначим: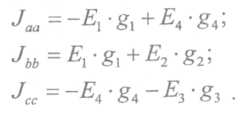

(8)

Эти величины назовем узловыми токами. Они представляют собой алгебраические суммы произведений э.д.с. ветвей, примыкающих к узлу, на проводимости этих ветвей, причем, если э.д.с. направлена к узлу, соответствующее сла­гаемое имеет знак плюс.

Подставив введенные обозначения в уравнения (3), получим после преобразований, аналогичных (5):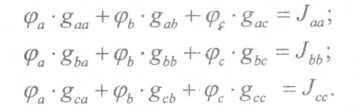

(9)

Получали систему расчетный уравнений по методу уз­ловых потенциалов, решив которую, можно найти потенци­алы всех узлов. Структура этой системы урав­нений аналогична системе уравнений по методу контурных токов, следовательно и методика решения такая же.

Практическое использование метода узловых потенци­алов сводится к тому, что после заземления одного из узлов схемы подсчитывают число оставшихся узлов, после чего сразу можно записывать систему уравнений, аналогичную (9). Затем по формулам (6), (7), (8) определяютзначения всех коэффициентов системы уравнений для за­данной конкретной схемы. После решения системы и опре­деления потенциалов узлов находим токи в ветвях по соот­ношениям (4).

Наиболее эффективно использование метода узловых потенциалов _ДЛя расчета сложных схем, имеющих много ветвей, но мало узлов.

Метод узловых потенциалов, как и метод контурных токов, относится к мощным расчётным методам, которые наиболее часто применяют для расчёта сложных схем, в т.ч. и на ЭВМ.

4)Мощность цепи постоянного тока. Баланс мощностей.

На основании закона сохранения энергии количество энергии, отдаваемой всеми источниками схемы, должно быть равно энергии, выделяемой на сопротивлениях схемы. Взяв расход энергии в единицу времени, перейдем к мощностям.

Для цепей постоянного тока уравнение баланса мощностей в электрической цепи:

п

(10)

В этом уравнении все слагаемые, в правой части всегда положительны. Действительно, на сопротивлениях энергия может только расходоваться. Иначе обстоит дело с источни­ки ЭДС. В случае, если направление ЭДС и направление тока через него совпадают, источник работает в режиме генератора и отдает электрическую энергию в схему. Однако могут быть случаи, когда направление тока через источник не совпадает с направлением ЭДС. В этом случае источник потребляет энергию (например, аккумуляторная батарея в режиме заряда). Соответствующие слагаемые в левой час­ти уравнения имеют знак минус.

Составление баланса мощности позволяет проверить правильность расчета схемы. Кроме того, знание отдельных слагаемых уравнения дает возможность наглядно представить распределение мощности на отдельных элемен­та схемы, определить мощность, отдаваемую каждым из источников, сравнив ее с номинальной или допустимой. Мощность на каждом из сопротивлений схемы позволяет оценить его нагрев. Ее также следует сравнить с номиналь­ной мощностью резистора, используемого в качестве сопротивления данной ветви.