лекции. Лекции Общая электротехника. Лекции по дисциплине Общая электротехника для студентов специальностей
 Скачать 4.27 Mb. Скачать 4.27 Mb.
|
|
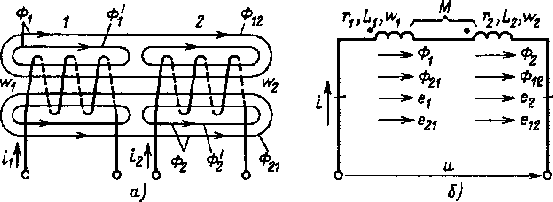
2) Последовательное соединение в цепи переменного тока На рис. 1,а, изображена электрическая цепь последовательно соединенных катушки индуктивности с активным сопротивлениемR и индуктивностью L и конденсатора с емкостью С. Активное сопротивление может также соответствовать сопротивлению какого-либо резистора.R, L и С- это параметры электрической цепи, причем активное сопротивление R характеризует активный (необратимый) процесс преобразования электрической энергии в другие виды энергии, а индуктивность L и емкость С - обратимый процесс преобразования энергии электромагнитного поля. Под действием напряжения u = Umsin t источника питания в цепи возникает ток i. Ток создает падения напряжения на элементах цепи: uR, Ri и на элементе с активным сопротивлением; на элементе с индуктивностью; 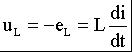 (6) (6)на элементе с емкостью. 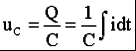 (7) (7)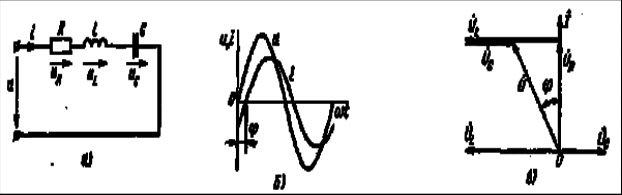 Рис. 1. Электрическая цепь при последовательном соединении элементов с R, L и С:а - схема; б - изменение напряжения и тока; в - векторная диаграмма напряжений и тока По второму закону Кирхгофадля данной цепи можно записать: 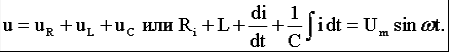 (8) (8)В результате решения уравнения (8) находится i(t).Полным решением линейного дифференциального уравнения (8) с постоянными коэффициентами является сумма частного решения этого уравнения и общего решения однородного дифференциального уравнения 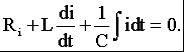 (9) (9)Уравнение (9) записано по второму закону Кирхгофа для цепи с последовательным соединением элементов R, L и С, когда напряжение источника питания равно нулю, т. е. когда электрическая цепь замкнута накоротко и электрическая энергия извне в цепь не поступает. В этих условиях ток в цепи может существовать только за счет запасов энергии в магнитном поле катушки или в электрическом поле конденсатора. При протекании тока через элемент с сопротивлением R происходит преобразование электроэнергии в тепловую и рассеяние ее в окружающую среду. Поэтому через некоторое время запасы электроэнергии будут израсходованы. Иными словами, ток, найденный в результате решения уравнения (9), через некоторое время будет равен нулю.Время, в течение которого существует этот ток, является временем переходного процесса в цепи и обычно исчисляется долями секунды. 3) Параллельное соединение в цепи переменного тока Проведем анализ работы электрической цепи с параллельным соединением элементов R, L, С. Рассмотрим следующую схему. 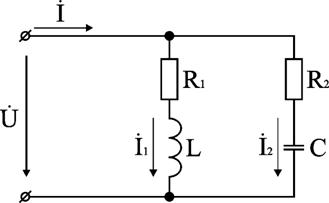 Рис.2 Электрическая цепь с параллельным соединением элементов R, L, С. Положим, что заданы величины R1, R2, L, С, частота f и входное напряжение U. Требуется определить токи в ветвях и ток всей цепи. В данной схеме две ветви. Согласно свойству параллельного соединения, напряжение на всех ветвях параллельной цепи одинаковое, если пренебречь сопротивлением подводящих проводов. Задача разбивается на ряд этапов 1. Определение сопротивлений ветвей. Реактивные сопротивления элементов L и С определяем по формулам XL = ωL, XC = 1 / ωC, ω = 2πf. Полное сопротивление ветвей равны , , соответствующие им углы сдвига фаз φ1 = arctg(XL / R1), φ2 = arctg(XС / R2). 2. Нахождение токов в ветвях. Токи в ветвях находятся по закону Ома I1 = U / Z1, ψi1 = ψu + φ1, I2 = U / Z2, ψi2 = ψu + φ2. 3. Нахождение тока всей цепи. Ток всей цепи может быть найден несколькими методами: графическим, методом мощностей, методом проекций и методом проводимостей. Чаще всего используют метод проекций и метод проводимостей. В методе проекций ток I1 и I2 раскладываются по две ортогональные составляющие активную и реактивную. Ось активной составляющей совпадает с вектором напряжения U. Ось реактивной составляющей перпендикулярна вектору U (рис. 3). 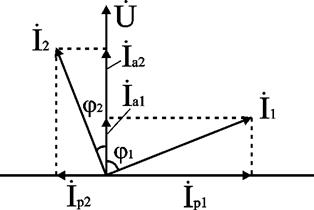 Рис.3 Метод проекций Активные составляющие токов равны I1а = I1 cosφ1, I2а = I2 cosφ2, (10) Iа = I1а + I2а. Реактивные составляющие токов равны I1р = I1 sin φ1, I2р = I2 sin φ2, (11) Iр = I1р - I2р. В последнем уравнении взят знак минус, поскольку составляющие I1р (индуктивная) и I2р (емкостная) направлены в разные стороны от оси U. Полный ток находится из уравнений: , (12) φ = arctg(Iр / Iа). (13) В методе проводимостей также используется разложение на активные и реактивные составляющие. Активные составляющие токов записываются в виде: 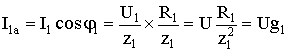 , (14) , (14)где через g1 = R1 / Z12 обозначена величина названная активной проводимостью первой ветви. Аналогичным образом получим: 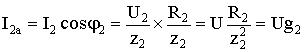 , (15) , (15)где g2 = R2 / Z22; а величину g = g1 + g2 называют активной проводимостью всей цепи. Реактивные составляющие токов: 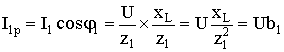 , ,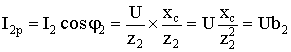 , ,где b1 и b2 – реактивные проводимости ветвей b1 = XL / Z12, b2 = XC / Z22. Для реактивной проводимости всей цепи имеем: b = b1 - b2. (16) Величина тока I и угол φ находятся из соотношений (11) , (12). (13) 4. Анализ расчетных данных. В зависимости от соотношения реактивных проводимостей b1 и b2 возможны три варианта: b1 > b2; b1 < b2; b1 = b2. Для варианта b1 > b2 имеем I1р > I2р, φ > 0. Цепь имеет активно-индуктивный характер. Векторная диаграмма изображена на рис. 4. 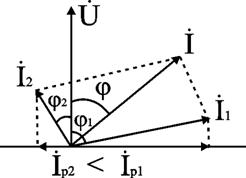 Рис. 4 Векторная диаграмма Рис. 4 Векторная диаграммаПриb1 < b2 токиI1р < I2р, φ < 0. Цепь имеет активно-емкостный характер. Векторная диаграмма изображена на рис. 5. 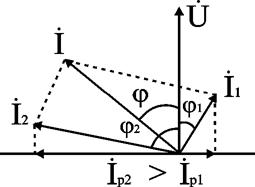 Рис. 5 Векторная диаграмма Если b1 = b2, то I1р = I2р, φ = 0. Цепь имеет чисто активное сопротивление. Ток потребляемый цепью от источника наименьший. Этот режим называется резонанс токов. Векторная диаграмма изображена на рис. 6. 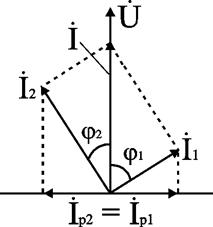 Рис. 6 Векторная диаграмма Лекция 6.Режимы работы электрических цепей 1) Мощность цепи переменного тока. Мгновенное значение мощности цепи синусоидального тока равно произведению мгновенных значений напряжения и тока:р =ui. Если к цепи приложено напряжение U=Umsinωt, то в общем случае ток в цепи:i= Imsin(ωt -φ) (рис. 1). Следовательно, р=UmImsinωtsin (ωt -φ) =2UI (sin2tcossintcostsin). После преобразований получим pUI [coscos (2t)].(1) Таким образом, мгновенное значение мощности имеет две составляющие: постояннуюUIcosω, не изменяющуюся во времени, и переменную UIcos (2tω) изменяющуюся периодически с частотой 2ω. Вследствие этого мгновенное значение мощности также изменяется с двойной частотой (рис. 1). При этом мощность положительна, если напряжение и ток совпадают по направлению, и отрицательна, если напряжение и ток имеют разные знаки. Когда мощность положительна, тогда электрическая энергия передается от источника к приемнику, и наоборот. 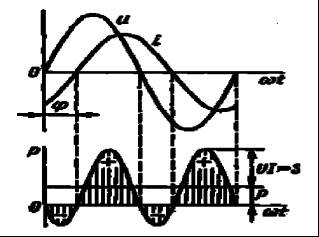 Рис. 1. Изменение напряжения, тока и мощности в цепи при последовательном соединении элементов с активным и реактивным сопротивлениями Для количественной оценки электроэнергетических процессов удобнее использовать среднее значение мощности Pcp, которое можно найти, вычислив работу, совершаемую за один период: 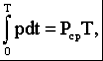 (2) (2)откуда 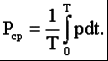 (3) (3)Подставив вместо р выражение (1), получим  Так как 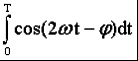 = 0, то = 0, то т. е. среднее значение мощности равно постоянной составляющей мгновенного значения мощности. Средняя мощность характеризует интенсивность передачи электроэнергии от источника к приемнику и ее преобразования в другие виды энергии, т. е. активный необратимый процесс. Поэтому среднюю мощность называют активной мощностью и выражают в ваттах, киловаттах и мегаваттах. P=UI сosω, (5) Активная мощность цепи синусоидального тока равна произведению действующих значений напряжения и тока и косинуса угла между их векторами. Для цепи, состоящей из элемента только с активным сопротивлением R pUI(1 cos2t). (6) Напряжение и ток (рис. 2, а)совпадают по фазе, и мгновенное значение мощности всегда положительно (рис. 2, б). Это указывает на то, что при наличии в цепи только элемента с активным сопротивлением вся электроэнергия преобразуется в тепловую или другие виды энергии. Среднее значение мощности или активная мощность Р=UI, так как cosω= 1. Поскольку напряжение Ua на элементе R совпадает по фазе с током (φ= 0), тоактивная мощность Р цепиможет быть определена как P Ua I R I2 U2a /R GU2a. 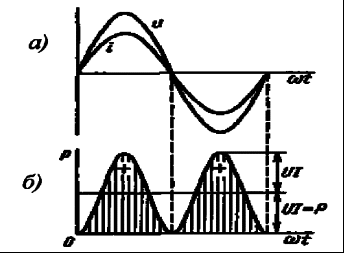 Рис 2. Изменение напряжения и тока: а) мощности; б) в цепи с активным сопротивлением В цепи с индуктивностью L угол φ=π/2 (рис. 3, а) и формула (1) принимает вид: рUIsin2t,(7) т. е. мгновенное значение мощности имеет только переменную составляющую (рис. 3. б). 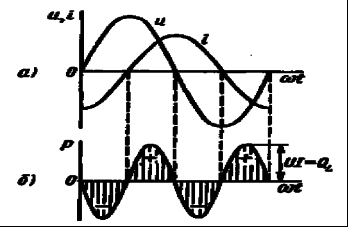 Рис. 3. Изменение напряжения и тока(а) и мощности (б) в цепи с индуктивностью Первую четверть периода ток совпадает по направлению с э. д. с. самоиндукции еLиндуктивной катушки, мощность отрицательна и энергия передается от катушки к источнику питания. Вторую четверть периода ток совпадает по направлению с напряжением источника питания, мощность положительна, а энергия поступает от источника к приемнику (индуктивной катушке) и запасается в его магнитном поле. В течение третьей четверти периода ток опять совпадает по направлению с eL и запасенная в магнитном поле катушки энергия передается источнику питания (мощность отрицательна). Таким образом, в течение одного периода электроэнергия дважды поступает от источника в катушку и обратно. При этом вся передаваемая энергия запасается в магнитном поле катушки и затем вся возвращается источнику. Такая энергия обмена между источником в приемником, которая не преобразуется в другие виды энергии, называется реактивной. Интенсивность обмена электроэнергией характеризуется реактивной мощностью QL, равной амплитуде мгновенного значения мощности, т. е. QL=UI. Реактивную мощность выражают в вольт-амперах реактивных (ВАр), киловольт-амперах реактивных (кВАр) и т. д. Напряжение на элементе с индуктивностью U = UL= XLI, поэтому реактивную мощность можно также определить по формулам: QL UL I XL I2 U2L/XL BL U2L, где BL= 1/XL - индуктивная проводимость. Если в цепь включен конденсатор с емкостью С, то φ= /2 (рис. 4., а) и мгновенное значение мощности P=UIsinωt, которое отличается от (7) только знаком. Изменение мощности для этой цепи показано на рис. 4, б. 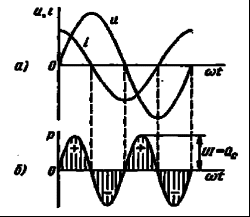 Рис 4. Изменение напряжения и токаа) и мощности б) в цепи с емкостью. В цепи с емкостью также происходит обмен электроэнергией между источником питания и конденсатором. При передаче энергии от источника питания в течение четверти периода энергия запасается в электрическом поле конденсатора, а в течение следующей четверти периода энергия электрического поля освобождается и возвращается источнику. Электроэнергетический процесс в цепи характеризуется только реактивной мощностью: QC=UCI=XCI2=U2C/XC=BCU2C, где BC=l/XC- емкостная проводимость. В общем случае, когда электрическая цепь состоит из элементов с активным R и реактивным X сопротивлениями, угол сдвига по фазе между напряжением и током в цепи φ= 0 -π/2 (рис. 1, а), а мгновенное значение мощности (рис. 1, б) описывается уравнением (1). Заштрихованная площадь, ограниченная положительным значением мощности и осью абсцисс, больше площади, ограниченной отрицательным значением мощности и осью абсцисс. Это означает, что в итоге часть электроэнергии передается от источника приемнику и преобразуется в нем в другие виды энергии. Количественно процесс преобразования электроэнергии оценивается активной мощностью (2). Составляющая мощности UIcos (2ωt-φ) изменяется с двойной частотой относительно линии, параллельной оси абсцисс и расположенной выше нее на значение активной мощности Р. Амплитуда UI переменной составляющей мощности называется полной мощностью и обозначается S. Полную мощность выражают в вольт-амперах (ВА), киловольт-амперах (кВА) и т. д. Ее можно вычислять по формулам SUIZI2U2/ZYU2 (8) где Y= 1/Z- полная проводимость цепи. То, что мгновенные значения мощности в некоторые промежутки времени принимают отрицательные значения, свидетельствует об обмене электроэнергией между источником питания и приемником электроэнергии. Обмен количественно оценивается реактивной мощностью Q=UPI. Так как в общем случае реактивная составляющая напряжения UP=Usinφ, то реактивная мощность цепи Q=UIsinφ. (9) Реактивная мощность цепи может быть вычислена как Q=XI2=U2P/X=BU2P, где В = 1/Х -реактивная проводимость цепи. Если цепь включает элементы и с индуктивным, и с емкостным сопротивлениями, то ее реактивное сопротивление XXL ХС, а Q (XLXC)I2XLI2XCI2QLQC. Таким образом, реактивная мощность цепи равна разности реактивной индуктивной и реактивной емкостной мощностей. Реактивная мощность положительна, если QL>QC, и отрицательна, если QC>QL. Соотношение между полной, активной и реактивной мощностями можно получить, воспользовавшись формулами (2), (4) и (5); Р2Q2 (UI)2 (cos2sin2) (UI)2S2, Следовательно, полная мощность равна корню квадратному из суммы квадратов активной и реактивной мощностей. Крометого, P S cos UI cos UAI; (10) Q S sin UI sin UPI.(11) Активная мощность определяется произведением составляющих напряжения и тока, совпадающих по фазе, а реактивная мощность - произведением составляющих напряжения и тока, находящихся в квадратуре (сдвинутых по фазена уголπ/2). Косинус угла сдвига фаз в формуле (4) называют коэффициентом мощности:cosφ=P/(UI) =P/S. Он показывает, какая доля полной мощности составляет активную мощность или какая доля всей электроэнергии преобразуется в другие виды энергии. Когда cos φ= 1, т. е. когда Z = R, активная мощность равна полной мощности. Коэффициент мощности - важный эксплуатационный параметр электроприемников. Так как I = Р/(Ucоsφ), то чем выше cоs φ, тем при меньшем значении тока в цепи может быть произведено преобразование электроэнергии в другие виды энергии. Это приводит к уменьшению потерь электроэнергии, ее экономии и удешевлению устройств электропередачи. 2) Резонансные режимы работы электрических цепей а) Общие сведения. Явление в электрической цепи синусоидального тока, содержащей участки с индуктивным и емкостным характером, при котором на входе цепи сдвиг фаз напряжения и тока равен нулю, называют резонансом. Математически это записывается в виде φ =ψu-ψi = 0. Резонансные явления представляют особый режим, при котором двухполюсник, несмотря на наличие реактивных элементов (индуктивностей и емкостей), выглядит как активное сопротивление (рис. 5), так как синусоидальные напряжение и ток совпадают по фазе. Резонансные явления широко применяются в электротехнических и радиотехнических устройствах автоматики, телемеханики, связи, измерительной техники. Из разновидностей резонансных явлений рассмотрим резонанс напряжений и резонанс токов. б) Резонанс напряжений. Условия резонанса напряжений. Резонансом напряжений называют явление резонанса на участке электрической цепи с последовательным соединением индуктивных и емкостных элементов.  а) б) Рис. 5 В простейшем случае указанный резонанс возможен при последовательном соединении катушки индуктивности, конденсатора и резистора; в радиотехнике такую цепь называют последовательным колебательным контуром. Представив эти элементы эквивалентными схемами, получим цепь (рис. 5,б), в которой R = Rpез+RL+Rc, а параметры Rpeз, RLи Rc отражают наличие потерь в резисторе, катушке индуктивности и конденсаторе соответственно. Рассмотрим условия возникновения резонанса напряжений. Из определения резонанса φ = arctg(X/R)= 0 следует, что в схеме рис. 5,б реактивное сопротивление: X = XL-Xc = 0, откуда XL=Xc или ω0L= 1/ω0С, где ωо — резонансная частота (частота, при которой возникает явление резонанса). Таким образом, условием возникновения резонанса напряжений является равенство индуктивного и емкостного сопротивлений. Поскольку эти сопротивления зависят от частоты и параметров, то для двух заданных величин из трех (ωo, L, С)резонанс может быть достигнут подбором третьей в соответствии с соотношениями:: L = 1/ω2oС,C =1/ω2oL. ωо = 1/√LC.(1) Следует подчеркнуть, что активное сопротивление не влияет на возникновение резонанса в последовательном колебательном контуре. в) Анализ резонанса напряжений. Проведем анализ схемы рис. 5,б, полагая частоту со источника ЭДС равной резонансной ω0- Полное сопротивление цепи равно активному и имеет минимальное значение. Сопротивления реактивных элементов на резонансной частоте ωо одинаковы: ωoL = 1/ωo С= √L/C (3) Сопротивление Zc не зависит от частоты и называется характеристическим сопротивлением контура. Ток в цепи, очевидно, будет максимальным и при неизменном напряжении Uисточника с учетом (2) составит:I = U/Z = U/R Напряжение и ток, как известно, совпадают по фазе, а цепь ведет себя как активное сопротивление. Напряжение на активном сопротивлении R равно напряжению источника:UR = RI = U. При последовательном соединении по элементам L иСпротекает одинаковый ток, а так как и XL = Xc= Zc, то напряжения на этих элементах одинаковы: UL = ωоL I = I/ ωoС = Uc = Zc U/R (4) и противоположны по фазе, компенсируя друг друга. При ZC>>R напряжения на реактивных элементах могут быть во много раз больше входного. На рис. 6 показаны векторные диаграммы тока и напряжений для резонансного режима при различных характеристических сопротивлениях. Равенство напряжений на реактивных элементах послужило названием явления резонанса напряжений. г) Добротность контура. Отношение напряжений на реактивных элементах при резонансе к напряжению источника или отношение характеристического сопротивления к активному сопротивлению контура называют добротностью контура UL (ω0)/U = Uс (ω0)/U = ZcR = Q. (5) Эта величина относительная и показывает, во сколько раз при резонансе напряжение на отдельных реактивных элементах больше входного. Добротность реального контура меньше добротностей отдельно взятых катушек индуктивности и конденсатора. Действительно, даже если предположить сопротивление резистора нулевым в схеме рис. 5,б., то 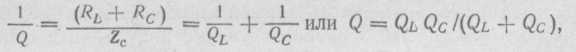 Где QL = Zc/RL — добротность катушки индуктивности; Qc = Zc/Rc — добротность конденсатора.< 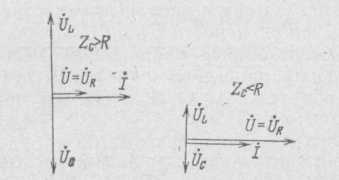 Рис.6 Векторные диаграммы тока и напряжений для резонансного режима Добротность Q будет всегда меньше наименьшей из двух величинQLиQc. е) Признаки резонанса напряжений. Резонанс напряжений может быть определен и опытным путем, по показаниям приборов (рис. 7). Признаки резонанса. 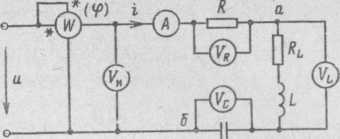 Рис.7 Прежде всего показания фазометра φ будут нулевыми, показаниями амперметра А в цепи — максимальными. Если пренебречь активными сопротивлениями катушки индуктивности (RL<<ωоL) и конденсатора (RС<< 1ωoС/), то входное напряжение и напряжение на резисторе R одинаковы, а напряжение UL= UC. Ваттметр покажет значение P = UI. Полная мощность S равна активной (средней), так как cosφ = 1. Резонанс напряжений используется на практике для усиления сигналов, для измерения параметров цепи или частоты. Однако при малых активных сопротивлениях на конденсаторах и катушках индуктивности возможны значительные перенапряжения на этих элементах, что нужно учитывать с точки зрения безаварийной работы устройства и безопасности лиц, обслуживающих эти устройства. Резонанс токов Резонансом токов называют явление резонанса на участке электрической цепи, содержащей параллельно соединенные ветви с индуктивными и емкостными элементами в разных ветвях. В радиотехнике простейшую электрическую цепь, состоящую из двух параллельных ветвей, одна из которых имеет индуктивный, а другая — емкостный характер, называют параллельным колебательным контуром. б) Резонанс токов в двухполюснике с потерями. Рассмотрим двухполюсник, образованный параллельными ветвями: одной с сопротивлением и емкостью, другой — сопротивлением и индуктивностью (рис. 8). Условие возникновения резонанса токов выражается в равенстве суммарной реактивной проводимости нулю: 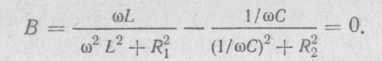 (6) (6)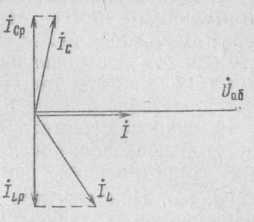 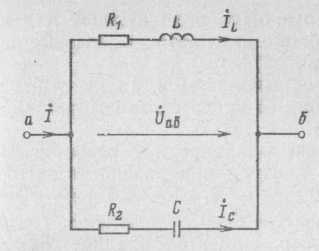 а) б) Рис. 8 Параллельный колебательный контур Резонанс токов можно получить изменением параметров ветвей R1, R2, L, С или частоты ω. Однако достичь этого не всегда удается. При четырех заданных величинах и пятой, определяемой из уравнения (6), ее значение может получиться мнимым или комплексным. Это свидетельствует о том, что при таком сочетании параметров резонанс токов невозможен. Решая уравнение (6) относительно частоты ω, получаем выражение резонансной частоты: 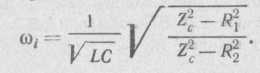 (7) (7)Чтобы резонансная частота была положительным действительным числом, необходимо иметь одновременно ZC>R1 и Zc>R2 или ZC Zс Если эти соотношения не выполняются, то не существует такой частоты (ωi- мнимое число), при которой возможен резонанс. Резонансная частота будет одинаковой с резонансной частотой последовательного контура при равенстве активных сопротивлений ветвей, т. е. R1 = R2 ≠ Zc. Ωi= ωо = 1/√LС. Наконец, при R1 = R2 = Zc = R резонанс токов наблюдается на любой частоте. При этом входное сопротивление контураявляется активным и не зависит от частоты. 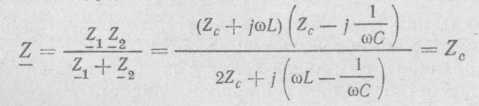 (8) (8)В общем случае при R1 При резонансе ток и напряжение совпадают по фазе (рис. 8,б), токи в параллельных ветвях не обязательно равны друг другу, а равны лишь их реактивные составляющие, ток I отличается от своих экстремальных значений. Из энергетических соотношений отметим, что максимальные значения энергии магнитного и электрического полей одинаковы, полная мощность равна активной, а реактивная мощность равна нулю. В устройствах систем электроснабжения резонанс токов предусматривается для увеличения cos φ, и это достигается путем параллельного подключения батарей конденсаторов к индуктивной нагрузке сети. Лекция 7.Соединение катушек со взаимной индуктивностью. Когда две катушки 1, 2 (рис. 1, а) расположены достаточно близко, так что часть Ф12магнитного потока Ф1 (Ф1 = Ф'1 + Ф12), создаваемого током первой катушки, пронизывает вторую, а часть Ф21 магнитного потока Ф2 (Ф2 = Ф'2 + Ф21), создаваемого током второй катушки, пронизывает первую, между катушками возникает магнитная связь 1. На схемах магнитная связь обозначается фигурной скобкой и буквой М (рис. 1, б). 1 Картина магнитных полей значительно сложнее, чем та, что условно изображена на рис. 1, а для пояснения явления взаимной индукции. Предполагается, что Ф12 и Ф21 — эквивалентные магнитные потоки, сцепленные соответственно со всеми витками w2, w1. Магнитная связь между катушками проявляется в том, что при изменении тока в катушках изменяются магнитные потоки и в катушках кроме ЭДС самоиндукции е1 = - w1 dФ1/dt, e2= - w2 dФ2/dt возникают ЭДС взаимной индукции: во второй катушке - от потока Ф12 е12 = - w2 dФ12/dt, в первой - от потока Ф21 е21 = -w2 dФ21/dt. Явление наведения ЭДС во втором контуре при изменении тока в первом называется явлением взаимной индукции. Рассмотрим контур, состоящий из двух соединенных последовательно катушек, согласно (потоки Ф1, Ф2 действуют в одном направлении) и встречно (потоки Ф1, Ф2 действуют встречно). Для обозначения согласного или встречного включения начала обмоток обозначаются жирными точками (рис. 1, б). Предполагается, что направления намотки катушек одинаковы (рис. 1, а). Результирующая ЭДС возникающая в контуре при изменении тока в нем: при согласном включении (рис. 1, б) еэк = е1 + е2 + е12 + е21; (1) при встречном включении еэк = е1 + е2 - е12 - е21. (2) ЭДС самоиндукции и взаимной индукции могут быть выражены соответственно через индуктивность L ивзаимную индуктивность М. Если индуктивность L устанавливает количественное соотношение тока в катушке и создаваемого им потокосцепления L = Ψ/I, то взаимная индуктивность М устанавливает количественное соотношение между током первой катушки и создаваемым им потокосцеплением со второй катушкой М12 = Ψ12/I1 и соответственноМ21 = Ψ21/I2.сцепления L = Ψ/I, то взаимная индуктивность М устанавливает количественное соотношение между током первой катушки и создаваемым им потокосцеплением со второй катушкой М12 = Ψ12/I1 и соответственно М21 = Ψ21/I2.
Рис. 1. К пояснению явления взаимной индукции(а), эквивалентная схема (б) Выразив в (1) и (2) соответствующие ЭДС через L и М иимея в виду, что M12 = M21 = M,получим 1: 1 Так как магнитные потоки Ф12, Ф21 расположены в одном и том же пространстве, магнитные сопротивления RM потокам будут одинаковыми и тогда Ф12 = I1w1/RM, Ф21 = I2w2/RM. Подставив Ф12 и Ф21 в выражения М12и М21, получим М12 = M21 = w1w2/RM = М. при согласном включении
при встречном включении (4) Сократив (3), (4) на di/dt, получим эквивалентные значения индуктивности контура Lэк: при согласном включении Lэк = L1 + L2 + 2M = L1 + L2 + 2k√L1L2;(5) при встречном включении Lэк = L1 + L2 - 2M = L1 + L2 - 2k√L1L2; (6) где
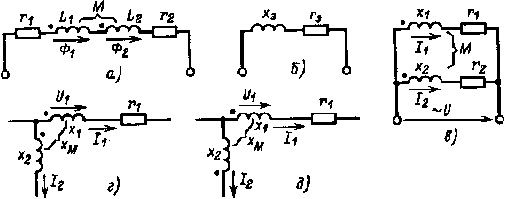
- коэффициент магнитной связи между контурами. Т. к. Ф12 < Ф1,Ф21 < Ф2, то k < 1. Умножив правые и левые части выражений (5), (6) на ω, получим: при согласном включении Lэкω = L1ω + L2ω + 2Мω, или хэк = х1 + х2 + 2хM; (7) при встречном включении хэк = х1 + х2 - 2хM; (8) где хэк - эквивалентное индуктивное сопротивление двух контуров, связанных взаимной индукцией; х1, х2 — индуктивные сопротивления, обусловленные индуктивностями L1 и L2; хM- индуктивное сопротивление, обусловленное взаимной индукцией М. Эквивалентное активное сопротивление в обоих случаях rэк = r1+ r2. Таким образом, электрическая цепь, состоящая из двух последовательно включенных, связанных взаимной индукцией катушек (рис. 2, а), может быть заменена эквивалентной цепью, изображенной на рис. 2, б. Определение токов в параллельно включенных катушках с r и L, связанных взаимной индукцией (рис. 2, в), производится с помощью совместного решения двух уравнений, составленных по второму закону Кирхгофа, I1(r1 + jx1)+ I2jxM = U; I2(r2 + jx2)+ I1jxM = U. Общий ток I = I1 + I2.
В сложных электрических цепях, когда две катушки, связанные взаимной индукцией, включены в разные ветви цепи (рис. 2, г, д),напряжение U1 имеет две составляющие, обусловленные собственной и взаимной индуктивностями: для схемы рис. 2, г U1 = I1jx1 + I2jxM; длясхемырис. 2, д U1 = I1jx1 - I2jxM; Знак плюс перед I2jxMозначает, что направление тока I2 такое же, что и тока I1: от начала к концу катушки. Во втором случае ток I2 имеет направление от конца к началу катушки, а ток I1 —от начала к концу катушки, поэтому перед I2jxMстоит знак минус. Лекция 8. Трехфазные цепи 1) Области применения трехфазных устройств, структура трехфазной цепи Трехфазная система была разработана в конце прошлого века известным русским электротехником М. О. Доливо-Добровольским. Она получила широкое распространение во всех странах мира. В настоящее время вся электроэнергия вырабатывается на электростанциях трехфазными генераторами, передается к местам потребления по трехфазным линиям передачи и основная ее доля используется в трехфазных приемниках. Преимущества трехфазной системы основываются, по мнению М. О. Доливо-Добровольского, главным образом на двух ее свойствах, которые используются при эксплуатации не только в совокупности, но и порознь. Это экономичная и на большие расстояния передача электроэнергии и превосходное качество двигателей. В устройствах выпрямления применяют шести- и двенадцатифазные системы, в устройствах автоматики и телемеханики двухфазные системы. Трехфазная система электрических цепей представляет собой совокупность электрических цепей, в которых действуют три синусоидальные э. д. с. одной и той же частоты, сдвинутые друг относительно друга по фазе и создаваемые общим источником энергии. 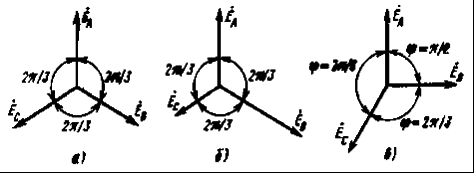 Рис. 1. Трехфазные системы э. д. с.:а - симметричная; б, в- несимметричная Если все три э. д. с. равны по значению и сдвинуты по фазе на 120° по отношению друг к другу, то такая система э. д. с. называется симметричной (рис. 1, а). Если э. д. с. не равны по значению (рис. 1, б) или сдвинуты друг относительно друга на угол, не равный 120° (рис. 1, в), то такая система э. д. с. называется, несимметричной. Аналогично определяются трехфазные системы напряжений и токов. |