лекции. Лекции Общая электротехника. Лекции по дисциплине Общая электротехника для студентов специальностей
 Скачать 4.27 Mb. Скачать 4.27 Mb.
|
|
Раздел 2. Электрические цепи переменного тока. Лекция 4. Основные понятия. Определения, характеристики 1) Основные понятия синусоидального тока. Средние и действующие значения тока, напряжения и ЭДС Широкое применение в электрических цепях электро-, радио- и других установок находят периодические э. д. с., напряжения и токи. Периодические величины изменяются во времени по значению и направлению, причем эти изменения повторяются через некоторые равные промежутки времени Т (рис. 1), называемые периодом. На практике все источники энергии переменного тока (генераторы электростанций) создают э. д. с., изменяющуюся по синусоидальному закону (рис. 5.1, д). 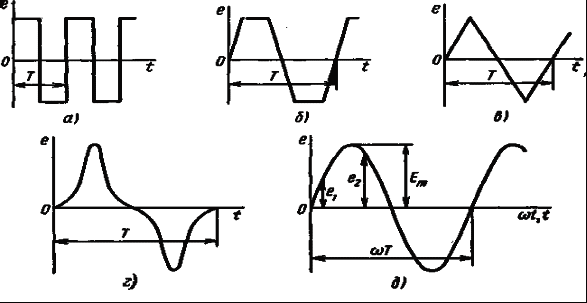 Рис. 1. Переменные периодические э. д. с. различной формы:а) - прямоугольный; б) - трапецеидальной; в) треугольной;г) - произвольной; д) - синусоидальной Основное преимущество такого закона изменения э. д. с. и напряжения заключается в том, что в процессе передачи электроэнергии на большие расстояния (сотни и тысячи километров) от источника до потребителя при многократной трансформации (изменении) напряжения временная зависимость напряжения остается неизменной, т. е. синусоидальной. Синусоидальные э. д. с. напряжения и токи начали широко применять в электротехнике во второй половине ХХ века. В настоящее время практически вся вырабатываемая электроэнергия является энергией синусоидального тока. Лишь некоторую долю этой электроэнергии при использовании преобразуют в энергию постоянного тока. Любая периодическая величина имеет ряд характерных значений. Максимальное значение или амплитуду э. д. с., напряжения и тока обозначают соответственно Еm, Um, Im. Значение периодически изменяющейся величины в рассматриваемый момент времени называют мгновенным ее значением и обозначают е, u, i э. д. с., напряжение и ток соответственно. Максимальное значение - частный случай мгновенного значения. Величина, обратная периоду, т. е. число полных изменений периодической величины за 1 с, называется частотой: f= 1/T. (1) Частоту выражают в герцах (Гц). Во всех энергосистемах России и других европейских стран в качестве стандартной промышленной частоты принята f = 50 Гц, в США и Японии f = 60 Гц. Это обеспечивает получение оптимальных частот вращения электродвигателей переменного тока и отсутствие заметного для глаза мигания осветительных ламп накаливания. Некоторые электротехнические устройства работают при более высокой частоте. Повышенная частота (обычно 175200, 400 Гц) позволяет снизить вес электродвигателей, применяемых для привода электроинструмента и средств автоматики. В установках сквозного нагрева металлов для горячей штамповки и ковки применяют частоту от 500 до 10 000 Гц, а в установках поверхностного нагрева металлов от 2000 до 106 Гц. В радиотехнических устройствах применяют частоты от 105 до 3 * 1010 Гц. Находят применение также синусоидальные токи пониженной частоты. Частоту f = 5 - 10 Гц применяют в металлургической промышленности. Электрические цепи, в которых действуют синусоидальные э. д. с. и токи, называются электрическими цепями синусоидального тока. К ним относятся понятия схемы цепи, контура, ветви и узла, которые были даны ранее для цепей постоянного тока. Как постоянный, так и синусоидальный токи используются для совершения какой-либо работы, в процессе которой электроэнергия преобразуется в другие виды энергии (тепловую, механическую и т. д.). Для количественной оценки синусоидального тока (э. д. с. и напряжения), который в течение времени непрерывно периодически изменяется, используют значение постоянного тока, эквивалентное значению синусоидального тока по совершаемой работе. Такое значение будет действующим для синусоидального тока. Исходя из этого условия действующим значением синусоидального тока называется такое значение постоянного тока, при прохождении которого в одном и том же резисторе с сопротивлением R за время одного периода Т выделяется столько же теплоты, сколько и при прохождении синусоидального тока. При синусоидальном токе i= Imsin*tколичество теплоты Qпер выделяемое в резисторе R за время Т, а при постоянном токеQпост=RI2T. (3) Согласно определению, Qпост= Qпер, тогда 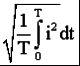 (4) (4)Таким образом, действующее значение синусоидального тока является его среднеквадратичным значением. Чтобы найти соотношение между максимальным и действующим значениями синусоидального тока, надо вычислить интеграл в формуле (5): 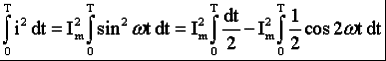 Так как 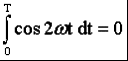 , получаем , получаем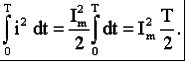 Подставляя это выражение в формулу (5), получим 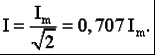 (5) (5)Аналогично, действующие значения э. д. с, и напряжений равны соответственно: 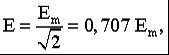 (6) (6)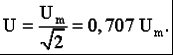 (7) (7)Действующие значения синусоидальных, величин в В большинстве электроизмерительных приборов, измеряющих ток и напряжение, используется принцип теплового, или электродинамического, эффекта. Поэтому они всегда показывают действующее значение, зная которое можно вычислить амплитуду по формулам (5) и (6). Так, например, если вольтметр показывает 220 В напряжения синусоидального тока, то амплитуда этого напряжения равна 2)Способы представления синусоидальных величин В современной технике широко используют разнообразные по форме переменные токи и напряжения: синусоидальные, прямоугольные, треугольные и др. Значение тока, напряжения, ЭДС в любой момент времени t называется мгновенным значением и обозначается малыми строчными буквами, соответственно: i = i(t); u = u(t); e = e(t). Токи, напряжения и ЭДС, мгновенные значения которых повторяются через равные промежутки времени, называют периодическими, а наименьший промежуток времени, через который эти повторения происходят, называют периодом Т. Если кривая изменения периодического тока описывается синусоидой, то ток называют синусоидальным. Если кривая отличается от синусоиды, то ток несинусоидальный. В промышленных масштабах электрическая энергия производится, передается и расходуется потребителями в виде синусоидальных токов, напряжений и ЭДС, При расчете и анализе электрических цепей применяют несколько способов представления синусоидальных электрических величин. 1. Аналитический способ Длятока: i(t) = Im sin(ωt + ψi), (8) для напряжения: (t) = Um sin (ωt +ψu), (9) для ЭДС: e(t) = Em sin (ωt +ψe), (10) В уравнениях (8 - 10) обозначено: - Im, Um, Em – амплитуды тока, напряжения, ЭДС; - значение в скобках – фаза (полная фаза); - ψi, ψu, ψe – начальная фаза тока, напряжения, ЭДС; - ω – циклическая частота, ω = 2πf; - f – частота, f = 1 / T; Т – период. Величины i, Im – измеряются в амперах, величины U, Um, e, Em – в вольтах; величина Т (период) измеряется в секундах (с); частота f – в герцах (Гц), циклическая частота ω имеет размерность рад/с. Значения начальных фаз ψi, ψu, ψe могут измеряться в радианах или градусах. Величина ψi, ψu, ψe зависит от начала отсчета времени t = 0. Положительное значение откладывается влево, отрицательное – вправо. 2. Временная диаграмма Временная диаграмма представляет графическое изображение синусоидальной величины в заданном масштабе в зависимости от времени (рис. 2). i(t) = Im sin(ωt - ψi). 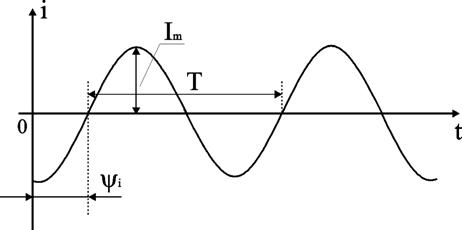 Рис.2 Временная диаграмма 3. Графоаналитический способ 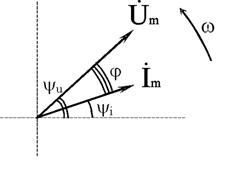 Рис. 3 Графическое изображение синусоидальной величины Графически синусоидальные величины изображаются в виде вращающегося вектора (рис. 3). Предполагается вращение против часовой стрелки с частотой вращения ω. Величина вектора в заданном масштабепредставляет амплитудное значение. Проекция на вертикальную ось есть мгновенное значение величины. Совокупность векторов, изображающих синусоидальные величины (ток, напряжение, ЭДС) одной и той же частоты называют векторной диаграммой. Векторные величины отмечаются точкой над соответствующими переменными. Использование векторных диаграмм позволяет существенно упросить анализ цепей переменного тока, сделать его простым и наглядным.В основе графоаналитического способа анализа цепей переменного тока лежит построение векторных диаграмм. Пример (рис. 4) 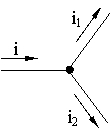 Рис. 4 Векторная диаграмма i1(t) = Im1 sin(ωt) i2(t) = Im2 sin(ωt + ψ2) i(t) = ? Первый закон Кирхгофа выполняется для мгновенных значений токов: i(t) = i1(t) + i2(t) = Im1 sin(ωt) + Im2 sin(ωt - ψ2) = Im sin(ωt + ψ). Приравниваем проекции на вертикальную и горизонтальные оси (рис. 5): Im sin ψ = Im2 sin ψ2; Im cosψ = Im2 cosψ2 + Im1; 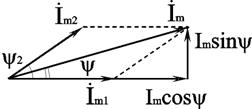 Рис. 5 Из равенств получаем: 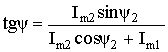 ; ;4. Аналитический метод с использованием комплексных чисел Синусоидальный ток i(t) = Im sin(ωt + ψ) можно представить комплексным числом Ím на комплексной плоскости (рис. 6): Ím = Imejψ,где амплитуда тока Im – модуль, а угол ψ, являющийся начальной фазой, – аргумент комплексного тока. 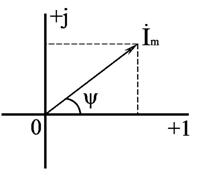 Рис. 6Синусоидальный токпредставленный комплексным числом Ím на комплексной плоскости Использование комплексной формы представления позволяет заменить геометрические операции над векторами алгебраическими операциями над комплексными числами. В результате этого к анализу цепей переменного тока могут быть применены все методы анализа цепей постоянного тока. 3) Элементы и их параметры в цепи переменного тока Индуктивность Вокруг всякого проводника с током образуется магнитное поле, которое характеризуется вектором магнитной индукции В и магнитным потоком Ф: . Если поле образуют несколько (w) проводников с одинаковым током, то используют понятие потокосцепления ψ: ψ = w Ф. (11) Отношение потокосцепления к току, который его создает называют индуктивностью катушки: L = ψ / i. (12) При изменении во времени потокосцепления согласно закону Фарадея возникает ЭДС самоиндукции: eL = - dψ / dt. С учетом соотношения (12) для eL получаем: eL = - L · di / dt.(13) Эта ЭДС всегда препятствует изменению тока (закон Ленца). Поэтому, чтобы через проводники все время тек ток, необходимо к проводникам прикладывать компенсирующее напряжение: uL = -eL. (14) Сопоставляя уравнения (13) и (14) получаем: uL = L · di / dt (15) Это соотношение является аналогом закона Ома для индуктивности. Конструктивно индуктивность выполняется в виде катушки с проводом. Условное обозначение индуктивности Катушка с проводом кроме свойства создавать магнитное поле обладает активным сопротивлением R. Условное обозначение реальной индуктивности. 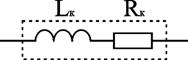 Единицей измерения индуктивности является Генри (Гн). Часто используют дробные единицы: 1 мкГн = 10–6 Гн; 1 мкГн = 10–3 Гн. Емкость Все проводники с электрическим зарядом создают электрическое поле. Характеристикой этого поля является разность потенциалов (напряжение). Электрическую емкость определяют отношением заряда проводника к напряжению: C = Q / UC. С учетом соотношения: i = dQ / dt получаем формулу связи тока с напряжением: i = C · duC / dt. Для удобства ее интегрируют и получают: uC = 1 / C · ∫ i dt. (16) Это соотношение является аналогом закона Ома для емкости. Конструктивно емкость выполняется в виде двух проводников разделенных слоем диэлектрика. Форма проводников может быть плоской, трубчатой, шарообразной и др. Единицей измерения емкости является фарада: 1Ф = 1Кл / 1В = 1Кулон / 1Вольт. Оказалось, что фарада является большой единицей, например, емкость земного шара равна ≈ 0,7 Ф. Поэтому чаще всего используют дробные значения 1 пФ = 10–12 Ф, (пФ – пикофарада); 1 нФ = 10–9 Ф, (нФ – нанофарада); 1 мкФ = 10–6 Ф, (мкФ – микрофарада). Условным обозначением емкости является символ Лекция 5. Законы Ома и Кирхгофа для цепей переменного тока 1) Законы Ома и Кирхгофа для цепей переменного тока Для цепей синусоидального тока также справедливы законы Кирхгофа, сформулированные ранее для цепей постоянного тока. Но так как синусоидальные величины (э. д. с., напряжение, ток) характеризуются мгновенными, максимальными и действующими значениями, то для каждого из них существуют свои формулировки законов Кирхгофа. Для мгновенных значений законы Кирхгофа справедливы в алгебраической форме. Первый закон состоит в том, что алгебраическая сумма мгновенных значений токов в узле равна нулю: 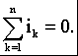 (1) (1)По второму закону алгебраическая сумма э. д. с. в контуре равна алгебраической сумме падений напряжений в этом контуре: 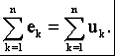 (2) (2)Для максимальных и действующих значений законы Кирхгофа справедливы только в векторной или комплексной форме. Согласно первому закону, сумма комплексных токов в узле равна нулю: 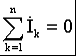 . (3) . (3)По второму закону сумма комплексных э. д. с. в контуре равна сумме комплексных падений напряжения в этом контуре: 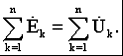 (4) (4)Второй закон Кирхгофа может быть сформулирован иначе: сумма мгновенных или комплексных значений падений напряжений на всех элементах контура, включая источники э. д. с., равна нулю: 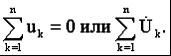 (5) (5)При составлении уравнений законов Кирхгофа в цепях синусоидального тока необходимо указать условное положительное направление э. д. с., задать условное положительное направление токов в ветвях и положительное направление падений напряжений на участках цепи, совпадающее с положительным направлением тока. Знак слагаемых в уравнениях определяется так же, как в цепях постоянного тока. Это относится как к мгновенным значениям синусоидальных величин, так и к комплексным. |
