лекции. Лекции Общая электротехника. Лекции по дисциплине Общая электротехника для студентов специальностей

• Название: Лекции по дисциплине Общая электротехника для студентов специальностей
• Анкор: лекции
• Дата: 17.04.2022
• Размер: 4.27 Mb.
• Имя файла: Лекции Общая электротехника.docx
• Тип: Лекции; #480717
• страница: 5 из 11

Раздел 3. Нелинейные элементы в цепях постоянного и переменного тока.
Лекция 10. Нелинейные элементы в цепях постоянного тока
1) Основные понятия. Нелинейные элементы и их ВАХ
Элементы электрических цепей, как известно, подразделяют на

активные и пассивные. К первым относятся источники электрической

энергии, источники сигналов. Пассивные элементы электрических

цепей — резисторы, катушки индуктивности, конденсаторы могут

быть, в свою очередь, разделены на линейные и нелинейные. Однако существует широчайшая группа так называемых нелинейных элементов, как пассивных, так и активных: нелинейные резисторы, конденсаторы, катушки индуктивности, электронные, ионные и полупроводниковые приборы, а также другие многочисленные элементы, основанные на принципах взаимодействия носителей тока с тепловыми, световыми и

электромагнитными полями, оптические квантовые генераторы и др.

Нелинейной считается цепь, содержащая хотя бы один нелинейный элемент. Нелинейными называются элементы, параметры которых зависят от величины и (или) направления связанных с этими элементами переменных (напряжения, тока, магнитного потока, заряда, температуры, светового потока и др.).

Цепи, содержащие только линейные элементы, называются линейными. Наличие в схеме хотя бы одного нелинейного элемента относит ее к классу нелинейных.

Рассмотрим пассивные элементы цепи, их основные характеристики и параметры.

1. Резистивный элемент (резистор)

Условное графическое изображение резистора приведено на рис. 1,а. Резистор – это пассивный элемент, характеризующийся резистивным сопротивлением. Последнее определяется геометрическими размерами тела и свойствами материала: удельным сопротивлением r (Ом) или обратной величиной – удельной проводимостью   (См/м).

В простейшем случае проводника длиной 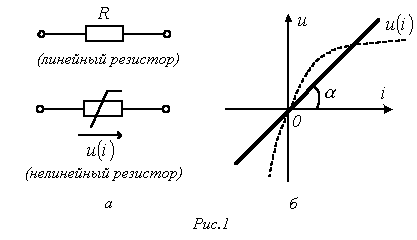  и сечением S его сопротивление определяется выражением

.


В общем случае определение сопротивления связано с расчетом поля в проводящей среде, разделяющей два электрода.

Основной характеристикой резистивного элемента является зависимость   (или  ), называемая вольт-амперной характеристикой (ВАХ). Если зависимость   представляет собой прямую линию, проходящую через начало координат (см.рис. 1,б), то резистор называется линейным и описывается соотношением



Или ,

Где   - проводимость. При этом R=const.

Нелинейный резистивный элемент, ВАХ которого нелинейна (рис. 1,б), как будет показано в блоке лекций, посвященных нелинейным цепям, характеризуется несколькими параметрами. В частности безынерционному резистору ставятся в соответствие статическое 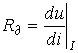  и дифференциальное   сопротивления.

2. Индуктивный элемент (катушка индуктивности)

Условное графическое изображение катушки индуктивности приведено на рис. 2,а. Катушка – это пассивный элемент, характеризующийся индуктивностью. Для расчета индуктивности катушки необходимо рассчитать созданное ею магнитное поле.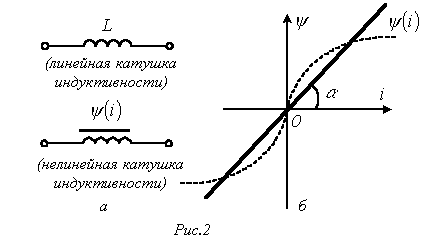



Индуктивность определяется отношением потокосцепления к току, протекающему по виткам катушки,

.

В свою очередь потокосцепление равно сумме произведений потока, пронизывающего витки, на число этих витков  , где  .

Основной характеристикой катушки индуктивности является зависимость  , называемая вебер-амперной характеристикой. Для линейных катушек индуктивности зависимость   представляет собой прямую линию, проходящую через начало координат (см. Рис. 2,б); при этом

.

Нелинейные свойства катушки индуктивности (см. Кривую 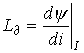  на рис. 2,б) определяет наличие у нее сердечника из ферромагнитного материала, для которого зависимость   магнитной индукции от напряженности поля нелинейна. Без учета явления магнитного гистерезиса нелинейная катушка характеризуется статической   и дифференциальной   индуктивностями.

3. Емкостный элемент (конденсатор)

Условное графическое изображение конденсатора приведено на рис. 3,а.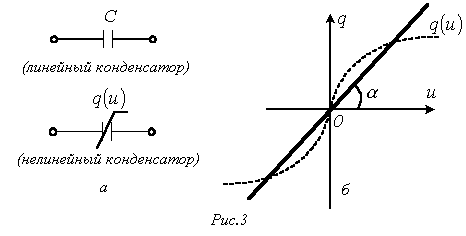



Конденсатор – это пассивный элемент, характеризующийся емкостью. Для расчета последней необходимо рассчитать электрическое поле в конденсаторе. Емкость определяется отношением заряда q на обкладках конденсатора к напряжению u между ними



И зависит от геометрии обкладок и свойств диэлектрика, находящегося между ними. Большинство диэлектриков, используемых на практике, линейны, т.е. У них относительная диэлектрическая проницаемость  =const. В этом случае зависимость   представляет собой прямую линию, проходящую через начало координат, (см. Рис. 3,б) и

.

У нелинейных диэлектриков (сегнетоэлектриков) диэлектрическая проницаемость является функцией напряженности поля, что обусловливает нелинейность зависимости 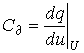  (рис. 3,б). В этом случае без учета явления электрического гистерезиса нелинейный конденсатор характеризуется статической   и дифференциальной   емкостями.
2) Статическое и дифференциальное сопротивления

Статическое и дифференциальное сопротивления. Свой­ства нелинейного резистора могут быть охарактеризованы либо его ВАХ» либо зависимостями его статического и дифференциального сопротивлений от тока (напряжений).

Статическое сопротивление характеризует поведение HP в режиме неизменного тока. Оно равно отношению напряжения на HP к протекающему но нему току:

Rст = U/I

Сопротивление R_ст численно равно тангенсу угла а между осью ординат и прямой, идущей в точку b (рис.4 а), умноженному на отношение масштабов по осям mu/mi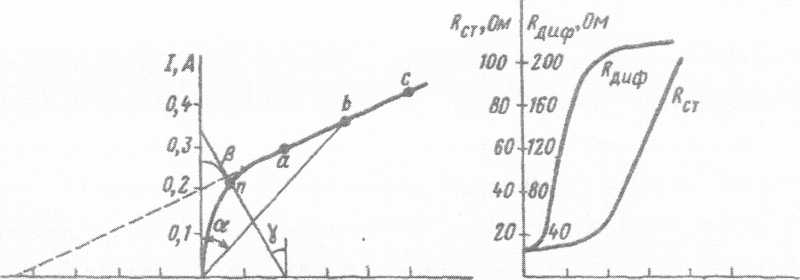

Рис.4
При переходе от одной точки ВАХ к соседней статическое сопро­тивление изменяется.

Под дифференциальным сопротивлением R_диф принято пони­мать отношение малого (теоретически бесконечно малого) прира­щения напряжения dUна HP к соответствующему приращению тока dI:

R_диф = dU/ dI

Дифференциальное сопротивление численно равно тангенсу уг­ла 0 (рис.4, а) наклона касательной к ВАХ в рабочей точке, умноженному на mu/mi. Оно характеризует поведение HP при до­статочно малых отклонениях от предшествующего состояния, т. е. приращение напряжения на HP связано с приращением тока, про­ходящего через него, соотношением dU = R_диф dI.

Таким образом, Rст — это сопротивление HP по постоянному току, а R_диф — по малой переменной составляющей.

3) Расчет нелинейных цепей.

Электрическое состояние нелинейных цепей описывается на основании законов Кирхгофа, которые имеют общий характер. При этом следует помнить, что для нелинейных цепей принцип наложения неприменим.В этой связи методы расчета, разработанные для линейных схем на основе законов Кирхгофа и принципа наложения, в общем случае не распространяются на нелинейные цепи.

Общих методов расчета нелинейных цепей не существует. Известные приемы и способы имеют различные возможности и области применения. В общем случае при анализе нелинейной цепи описывающая ее система нелинейных уравнений может быть решена следующими методами:

графическими;

аналитическими;

графо-аналитическими;

итерационными.

  Графические методы расчета

При использовании этих методов задача решается путем графических построений на плоскости. При этом характеристики всех ветвей цепи следует записать в функции одного общего аргумента. Благодаря этому система уравнений сводится к одному нелинейному уравнению с одним неизвестным. Формально при расчете различают цепи с последовательным, параллельным и смешанным соединениями.

а) Цепи с последовательным соединением резистивных элементов.

При последовательном соединении нелинейных резисторов в качестве общего аргумента принимается ток, протекающий через последовательно соединенные элементы. Расчет проводится в следующей последовательности. По заданным ВАХ  отдельных резисторов в системе декартовых координат  строится результирующая зависимость . Затем на оси напряжений откладывается точка, соответствующая в выбранном масштабе заданной величине напряжения на входе цепи, из которой восстанавливается перпендикуляр до пересечения с зависимостью . Из точки пересечения перпендикуляра с кривой  опускается ортогональ на ось токов - полученная точка соответствует искомому току в цепи, по найденному значению которого с использованием зависимостей  определяются напряжения  на отдельных резистивных элементах.

Графическое решение для последовательной нелинейной цепи с двумя резистивными элементами может быть проведено и другим методом -методом пересечений.В этом случае один из нелинейных резисторов, например, с ВАХ   считается внутренним сопротивлением источника с ЭДС Е, а другой - нагрузкой. Тогда на основании соотношения  точка а (см. рис. 3) пересечения кривых  и  определяет режим работы цепи. Кривая  строится путем вычитания абсцисс ВАХ  из ЭДС Е для различных значений тока.

Использование данного метода наиболее рационально при последовательном соединении линейного и нелинейного резисторов. В этом случае линейный резистор принимается за внутреннее сопротивление источника, и линейная ВАХ последнего строится по двум точкам.

б) Цепи с параллельным соединением резистивных элементов.

При параллельном соединении нелинейных резисторов в качестве общего аргумента принимается напряжение, приложенное к параллельно соединенным элементам. Расчет проводится в следующей последовательности. По заданным ВАХ  отдельных резисторов в системе декартовых координат  строится результирующая зависимость . Затем на оси токов откладывается точка, соответствующая в выбранном масштабе заданной величине тока источника на входе цепи (при наличии на входе цепи источника напряжения задача решается сразу путем восстановления перпендикуляра из точки, соответствующей заданному напряжению источника, до пересечения с ВАХ ), из которой восстанавливается перпендикуляр до пересечения с зависимостью . Из точки пересечения перпендикуляра с кривой  опускается ортогональ на ось напряжений - полученная точка соответствует напряжению на нелинейных резисторах, по найденному значению которого с использованием зависимостей  определяются токи  в ветвях с отдельными резистивными элементами.

Лекция 11. Магнитные цепи
1) Основные понятия теории электромагнитного поля и основные магнитные величины

Источники и приемники электрической энергии в общем случае представляют собой электромагнитные устройства, работающие на основе использования магнитного поля. Последнее обычно описы­вается величинами магнитной индукции, магнитного потока, намаг­ниченности, напряженности магнитного поля, магнитной проница­емости.

Вектор магнитной индукции В определяют по силе F, действующей на электрический заряд q перемещающийся в магнитном поле со скоростью v:

F = q [v В].(1)

Для проводника длиной l с током I это равнозначно выражению F=[Bi]l

где направление силы соответствует правилу левой руки: (магнитные силовые линии В упираются в ладонь, выпрямленные четыре пальца располагаются по направлению тока i, отогнутый большой палец показывает направление электромагнитной силы F)

Действие магнитного поля (индукции В) называют электромеханическим или силовым, а выражение (1) - законом электромагнитных сил.

Другим действием магнитного поля является индукционное, выражающиеся в возникновении электродвижущей силы (ЭДС) е при перемещении проводника со скоростью v в этом магнитном поле с индукцией В:

е = (Bv)l

При этом направление эдс е определяется правилом правой руки (магнитные силовые линии В упираются в ладонь, отогнутый большой палец показывает направление движения проводника (на­правление вектора скорости v) эффективной длины l, выпрямлен­ные четыре пальца — направление ЭДС e) В международной системе СИ магнитная индукция измеряется в теслах [Тл]. Выражение (1) иногда называют законом электромагнитной индукции.

Если магнитное поле (индукция В) переменное, то в неподвижном проводнике, находящемся в этом поле, наводится ЭДС индукции. На этом основаны устройства трансформаторов, генераторов, электроиз­мерительных приборов, преобразователей и все расчеты при их про­ектировании. Электромеханическое (силовое) действие магнитного поля используется для создания электродвигателей, тяговых устройств, электромагнитных муфт и реле, электроизмерительных приборов.

Магнитный поток Ф есть поток вектора магнитной индукции В через площадь S:

Ф = ∫BdS,

s

Где ds - элемент поверхности s при однородном магнитном поле (в = const), перпендикулярном площадке, ф = bs.

В системе си магнитный поток ф измеряется в веберах (вб), при этом 1 вб = 1 тл • м².

Намагниченность м - это магнитный момент единицы объема v вещества:

м = lim σm/v,

v→0

где т = is есть вектор магнитного момента элементарного контура тока [ам2]; i - ток контура, s- вектор площадки, ограниченной контуром тока.

Наряду с вектором намагниченности м используется вектор напряженности магнитного поля

h = 1/4πgrad ∫mr0 /r₀

v

Где r₀ - радиус-вектор, направленный от точки расположения элементарного контура тока к точке наблюдения.

Намагниченность м и напряженность h являются силовыми характеристиками магнитного поля с размерностью [а/м]; для напряженности магнитного поля н, в частности, выбрано исходное соотношение н = in/l, где i - ток через сечение длиной l с числом витков n. Векторы в, м, н связаны соотношением

в = μ0(н + м),

Где μ0 =4π*10^-7 [гн/м] — магнитная постоянная, абсолютная магнит­ная проницаемость вакуума, которая совместно с абсолютной маг­нитной проницаемостью μ среды определяет используемую в рас­четах относительную магнитную проницаемость среды

μr = μm/μо; здесь μm = в/н [гн/м],

При этом μr = в/в0,

Где н - напряженность магнитного поля в данной точке, в - маг­нитная индукция в этой точке поля при наличии среды с абсолют­ной магнитной проницаемостью μm, в0 - магнитная индукция в той же точке поля в вакууме.

из последнего соотношения следует, что относительная магнитная проницаемость μr среды является величиной, показывающей во сколько раз магнитная индукция в поля в данной среде отличается от магнитной индукции поля в вакууме.

Применение магнитопроводов с абсолютной магнитной проводимостью μ в различных электромагнитных устройствах позволяет усилить интенсивность магнитного поля н в μ раз в некоторой час­ти объема таких устройств, а также за счет преломления магнитных силовых линий на границах раздела магнитопровода (ферромагнит­ной среды) и другой среды (воздух, вода, масло), в этом объеме создавать целесообразную топографию магнитного поля.
2) Определения классификация и свойства магнитных цепей, законы магнитных цепей

При подключении к обмотке катушки с числом витков W(рис.1) переменного напряжения u(t) по обмотке будет протекать переменный ток i(t) и создавать переменный магнитный поток

Ф = Фст+Фσ, <1Л65>

Где Фст — основная часть магнитного потока, замыкающаяся по

магнитопроводу; Фσ - часть магнитного потока, замыкающаяся по неферромагнитной среде (воздуху), называемая потоком рассеяния.

Образованный магнитный поток, пересекая витки обмотки, на­водит в ней ЭДС самоиндукции, которая совместно с падением на­пряжения на активном сопротивлении обмотки R будет уравнове­шивать приложенное напряжение: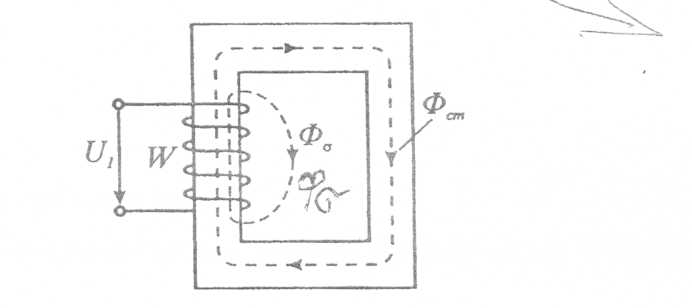



Рис. 1. Катушка индуктивности с магнитопроводом
3) Магнитные цепи с постоянными магнитными потоками

Магнитная цепь (МЦ) – часть электротехнического устройства, предназначенного для создания в определенном месте пространства магнитного поля требуемой интенсивности и направленности. Магнитные цепи составляют основу практически всех электротехнических устройств и многих измерительных приборов. В составе МЦ имеются элементы, возбуждающие магнитное поле (одна или несколько намагничивающих обмоток или постоянные магниты) и магнитопровод, выполненный в основном из ферромагнитных материалов. Использование ферромагнетиков обусловлено их способностью многократно усиливать внешнее (по отношению к ним) магнитное поле, создаваемое намагничивающими обмотками или постоянными магнитами. Ферромагнетики отличает высокая магнитная проницаемость по сравнению с окружающей средой, что дает возможность концентрировать и направлять магнитные поля.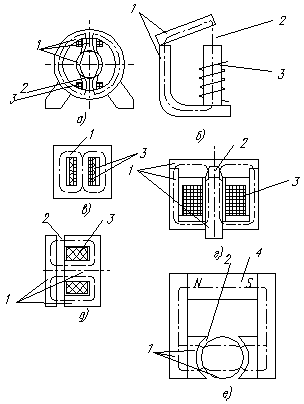 


Рис. 2 МЦ некоторых электромагнитных устройств: а – машин постоянного тока, б – электромагнитного реле, в – трансформатор, г и д – тормозных электромагнитов, е – магнитоэлектрического измерительного прибора. Цифрой 1- обозначены ферромагнитные части магнитопроводов, 2 – воздушные зазоры, 3 – намагничивающие катушки, 4 – постоянный магнит. 


МЦ с постоянной МДС называются цепи, в которых магнитное поле возбуждается постоянными токами намагничивающих обмоток или постоянными магнитами.

При анализе и расчете магнитных цепей пользуются следующими величинами, характеризующими магнитное поле:

 – вектор магнитной индукции. Характеризует интенсивность и направленность магнитного поля в данной точке пространства. Единица измерения – тесла(1 Тл = ).

– вектор напряженностимагнитного поля в данной точке. Единица измерения – ампер на метр ( ). 

Отношение   – абсолютная магнитная проницаемость. Для вакуума, а также для любых неферромагнитных материалов принимается равной

 m₀=4π·10^-7 Гн/м; отношение 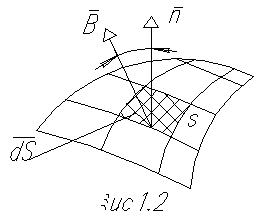  – относительная магнитная проницаемость ( для конкретных ф ерромагнетиков может доходить до 10⁴ – 10⁶ ).

Рис. 3

Ф – магнитный поток– поток вектора магнитной индукции через площадь S (рис. 3), единица измерения вебер(1Вб=1Тл×1м²)

 
В случае однородного магнитного поля, когда B=const в любой точке поля и вектор магнитной индукции  ^S (Ða = 0), магнитный поток Ф = B×S.

Расчет магнитной цепи невозможен, если неизвестна основная кривая намагничивания (ОКН) ферромагнетика, используемого в магнитопроводе.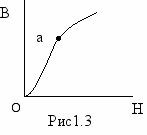



Рис. 4.

ОКН задается в справочной литературе на электротехнические материалы как зависимость В(Н) либо в табличной форме, либо графически (рис.4).

Отметим, что на участке оа, отношение  const. – магнитная цепь не насыщена. При дальнейшем увеличении Н темп увеличения индукции В снижается и прекращается полностью, когда наступает магнитное насыщение материала магнитопровода.

4) Нелинейные элементы в цепях переменного тока.

Нелинейные сопротивления для переменного тока можно подразделить на три группы: активные, индуктивные и ёмкостные. Каждая из этих групп, в свою очередь, делится на управляемые и неуправляемые.

Управляемые нелинейные сопротивления обычно имеют один или несколько управляющих электродов или управляющих обмоток, включаемых в управляющую цепь или цепи, воздействуя на ток или напряжение которых, можно управлять величиной сопротивления в главной цепи.

Наиболее широкое распространение в качестве управляемых нелинейных активных сопротивлений получили полупроводниковые триоды (транзисторы) и тиристоры.

Неуправляемыми нелинейными активными сопротивлениями являются полупроводниковые диоды, термисторы и другие элементы.

К нелинейным элементам в цепях переменного тока также относятся: индуктивные катушки с ферромагнитными сердечниками, работающие в условиях магнитного насыщения; электронные приборы; конденсаторы с  сегнетодиэлектриками, у которых диэлектрическая проницаемость зависит от величины приложенного напряжения.

Вышеотмеченные нелинейные элементы используются в устройствах, предназначенных для преобразования переменного тока в постоянный, постоянного в переменный , стабилизации напряжения и тока, усиления мощности электрических сигналов, деления и умножения частоты и т. д.

Под нелинейной индуктивностью понимают катушку индуктивности, намотанную на замкнутый сердечник из ферромагнитного материала (например, электротехническая сталь), для которого зависимость магнитного потока в сердечнике от протекающего по обмотке тока нелинейная. Индуктивное сопротивление такой катушки перемененному току непостоянно; оно зависит от величины переменного тока.

Катушку индуктивности со стальным сердечником в литературе называют иногда дросселем со стальным сердечником.

Обозначение её на принципиальной схеме имеет вид  .

В обычных конденсаторах обкладки разделены веществом, диэлектрическая проницаемость которого не является функцией напряжённости электрического поля, поэтому ёмкость таких конденсаторов не зависит от напряжения.

У нелинейных конденсаторов ёмкость С зависит от напряжения U, на электрических принципиальных схемах они имеют обозначение   , называются они ещё варикондами.