лекции. Лекции Общая электротехника. Лекции по дисциплине Общая электротехника для студентов специальностей

• Название: Лекции по дисциплине Общая электротехника для студентов специальностей
• Анкор: лекции
• Дата: 17.04.2022
• Размер: 4.27 Mb.
• Имя файла: Лекции Общая электротехника.docx
• Тип: Лекции; #480717
• страница: 4 из 11

Часть трехфазной системы электрических цепей, в которой может протекать один из токов трехфазной системы, называется фазой. Таким образом, фазой являются обмотка генератора, в которой индуцируется э. д. с., и приемник, присоединенный к этой обмотке. Это значение термина «фаза» широко используется в практической электротехнике.
2) Получение трехфазной системы э. Д. С.

Трехфазная система э. д. с. создается трехфазными генераторами. В неподвижной части генератора (статоре) размещают три обмотки, сдвинутые в пространстве на 120° (рис. 2, а). Это фазные обмотки, или фазы, которые обозначают А, B и С. Этими же буквами обозначают начало обмоток фаз генератора. Концы обмоток обозначают соответственно X, Y и Z. На рис. 2, б показано, как изображают на схемах обмотки генератора с условными положительными направлениями э. д. с.



Рис. 2. Схема трехфазного, генератора (а) и изображение фазных обмоток генератора на схемах (б)

Каждая фазная обмотка генератора изображена на рис. 2, а одним витком (у реальных генераторов каждая обмотка имеет множество витков, расположенных в нескольких соседних пазах, занимающих некоторую дугу внутренней окружности статора). На вращающейся части генератора (роторе) располагают обмотку возбуждения, которая питается от источника постоянного тока. Ток обмотки возбуждения создает магнитный поток Ф₀, постоянный (неподвижный) относительно ротора, но вращающийся вместе с ним с частотойn. Вращение ротора осуществляется каким-либо двигателем.

Благодаря конструктивным приемам магнитный поток Ф₀ в воздушном зазоре между статором и ротором распределяется по синусоидальному закону по окружности. Поэтому при вращении ротора вращающийся вместе с ним магнитный поток пересекает проводники обмоток статора (А- X, В- Y и С- Z) и индуцирует в них синусоидальные э. д. с. В момент времени, которому соответствует изображенное на рисунке взаимное положение статора и ротора, в обмотке фазы А индуцируется максимальная э. д. с. Е_m, так как плоскость этой обмотки совпадает с осевой линией полюсов ротора и проводники обмотки пересекаются магнитным потоком максимальной плотности. Через промежуток времени Т/3, соответствующий 1/3 оборота ротора, осевая линия его полюсов совпадает с плоскость. обмотки фазы В и максимальная э. д. с. Е_m индуцируется в фазе В. Еще через 1/3 оборота ротора максимальная э. д. с. индуцируется в фазе С. При следующих оборотах ротора процесс повторяется.

Таким образом, э. д.с. в каждой последующей фазе будет отставать от э. д. с. в предыдущей фазе на 1/3 периода, т. е. на угол 2π/3. Если принять, что для фазы А начальная фаза равна нулю, то э. д. с. фазы Ае_аЕ_тsint,а э. д. с. фаз В и С соответственно: е_вЕ_тsin (t 2/3);е_сЕ_тsin (t 4/3).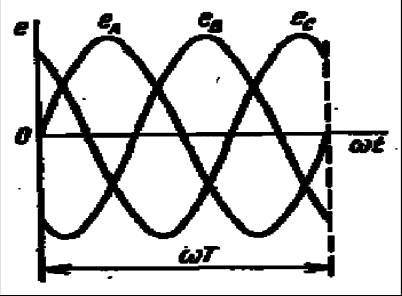



Рис. 3. Изменение мгновенных значений трехфазной системы э. д. с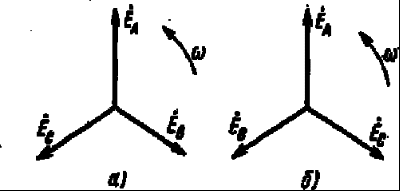



Рис. 4. Векторы трехфазной системы э. д. с. при прямом (а) и обратном (б)чередовании фаз

Максимальные (амплитудные) значения всех э. д. с. и их частоты будут одинаковыми, так как число витков фазных обмоток одинаково и э. д. с. индуцируются одним потоком Ф₀. Изменение фазных э. д. с. е_а, е_в и е_с показано на рис. 3.

Действующее значение фазной э. д. с. трехфазной системы определяется по формуле: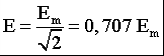



При равных амплитудах действующие значения э. д. с. всех фаз равны. При сдвиге по фазе на 2/3 они образуют симметричную систему. Если при условном положительном направлении вращения векторов (против часовой стрелки) вектор э. д. с. Е_в отстает по фазе от вектора э. д. с. Е_а, а вектор э. д. с. Е_с отстает по фазе от вектора э. д. с. Е_в, то такая система векторов э. д. с. образует прямое чередование фаз (рис. 4, а).Если за вектором э. д. с Е_А следует сначала вектор э. д. с. Е_С, а затем вектор э. д. с. Е_В, то такая система векторов э. д. с. образует обратное чередование фаз (рис..4, б).

При представлении трехфазной системы э. д. с. комплексными числами принято э. д. с. фазы А совмещать с положительным направлением вещественной оси (рис. 5). Тогда при прямом чередовании фаз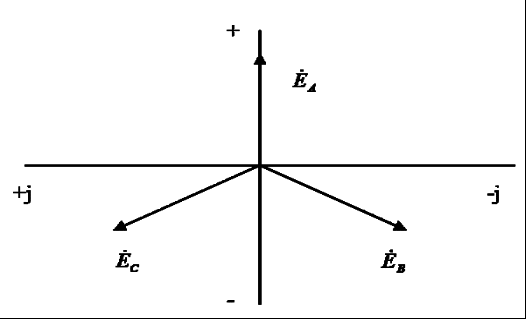

^{, (1)}



Рис. 5. Изображение трехфазной системы э. д. с. в комплексной плоскости

<sup>(2),

(3).</sup>

где Е- действующее значение э. д. с.

При симметричной системе э. д. с., как это видно из рис. 5. и формул (1), (2), (3), векторная сумма э. д. с. равна нулю:
3) Соединение обмоток генератора и фаз приемника звездой

Каждая фаза трехфазного генератора может являться источником питания для однофазного приемника. В этом случае схема электрической цепи имеет вид, изображенный на рис. 9.6, т. е. каждая фаза работает отдельно от других, хотя в целом цепь является трехфазной. Это трехфазная несвязанная система.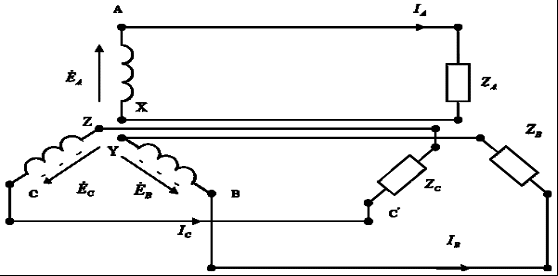



Рис. 6. Схема трехфазной несвязанной электрической цепи

Э. д. с. любой обмотки генератора представляет собой разность потенциалов начала и конца этой обмотки. При этом потенциал одной какой-либо точки (или начала, или конца обмотки) можно считать равным нулю. Тогда комплексный потенциал другой точки будет иметь точно определенное значение.

Принимая равными потенциалы точек, соответствующих концам X, Y и Z обмоток фаз генератора, можно объединить их в одну точку N (рис. 7).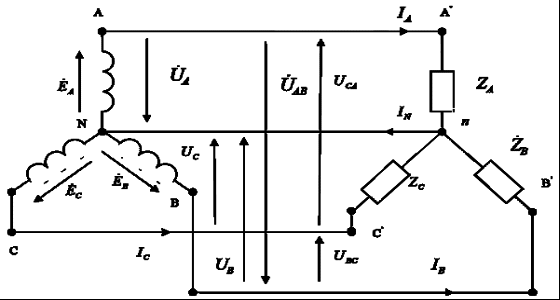



Рис. 7. Схема связанной четырех проводной трехфазной цепи

<sup>Концы фаз приемников (ZA, ZB и ZC) также соединены в одну точку n. Такое соединение обмоток генератора называется соединением «звездой»

( ). Звездой можно соединять также фазы приемника. Точки N и n называется нейтральными, а провод, соединяющий точку N генератора с точкой n приемника,  нейтральным. Провода АА', ВВ' и СС', соединяющие начала фаз генератора и приемника, называются линейными.</sup>

Напряжение между началом и концом фазы  фазное напряжение U_ф.

Напряжение между линейными проводами  линейное напряжение U_л.
4) Соединение обмоток генератора и фаз приемника треугольником

^{Соединение обмоток генератора или фаз приемника, при котором начало одной фазы соединяется с концом другой, образуя замкнутый контур, называется соединением «треугольником» ( 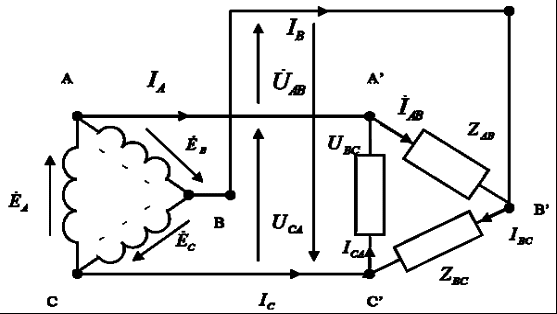). Начало фазы А источника питания соединяют с концом фазы B (Y) и точку соединения обозначают А (рис. 8). Далее соединяют точки В и Z (точка В) и точки С и X (точка С). Положительные направления э. д. с. в обмотках те же, что и на рис. 9.6. Подобным образом соединяют треугольником и фазы приемника, сопротивления которых обозначены двумя индексами, соответствующими началу и концу фазы.}



Рис. 8. Схема трехпроводной трехфазной цепи при соединении фаз треугольником

Лекция 9
1) Назначение нейтрального провода

Рассмотрим трехфазную цепь при соединении обмоток генератора и фаз приемника звездой (рис. 1). В обмотках генератора индуцируется симметричная система э. д. с. Пренебрегая потерями напряжения в обмотках, можно считать, что системы фазных ( 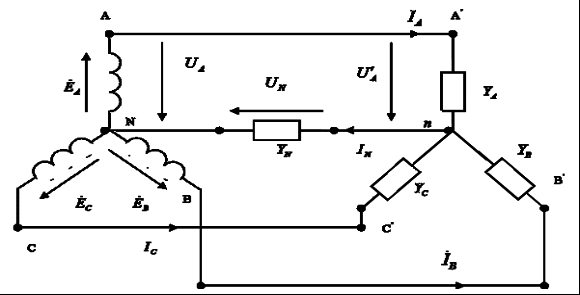, , ) и линейных , , ) напряжений генератора симметричны и неизменны. Сопротивления линейных проводов примем равными нулю.



Рис. 1. Схема трехфазной цепи с нейтральным проводом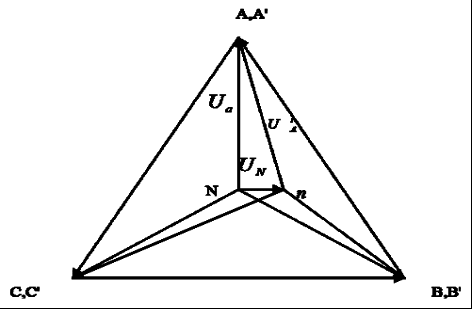



Рис. 2. Векторная диаграмма напряжений трехфазной цепи с нейтральным проводом

Тогда система линейных напряжений ( , , ) приемника будет совпадать с системой линейных напряжений генератора.

Соединенные звездой фазы приемника представлены комплексными проводимостями: , , . Нейтральный провод в общем случае имеет проводимость . На рисунке указаны также положительные направления фазных токов , , и тока . Как на фазе приемника, так и на элементе условное, положительное направление падения напряжения совпадает с направлением тока (на рис. 10.5 напряжения указаны только для фазы А).

Электрическая цепь состоит из параллельных ветвей с источниками э. Д. С. И одной параллельной ветви (нейтральный провод) с пассивным элементом. Напряжение на этой ветви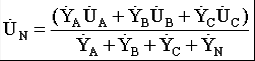

. (1)

На рис. 2 построена векторная диаграмма напряжений генератора и приемника. Как указывалось, системы фазных и линейных напряжений генератора симметричны и неизменны, точка N лежит в центре тяжести равностороннего треугольника ABC. Линейные напряжения приемника равны линейным напряжениям генератора, потенциалы точек А и А', В и В', С и С' соответственно равны.

На диаграмме потенциал точки N равен нулю и начало осей комплексной плоскости совпадает с этой точкой на векторной диаграмме фазных напряжений генератора. Векторы, фазных напряжений , , направлены от точки N к точкам А, В и С. Потенциалам этих точек на схеме рис. 1 соответствуют комплексные числа в точках А, В и С на векторной диаграмме напряжений.

^{При заданных проводимостях фаз приемника и нейтрального провода по можно найти напряжение} между точками N и n. Вектор напряжения будет направлен из точки N векторной диаграммы, причем его концу будет соответствовать потенциал точки n приемника. Фазное напряжение приемника - это напряжение между точками А' и n. Поэтому на диаграмме ^{вектор напряжения будет направлен от точки n к точке А'. Аналогично строят фазные напряжения и .}

Построенные таким образом векторы напряжений для фазы A полностью удовлетворяют уравнению, написанному для контура фазы А.



Точка n на векторной диаграмме в зависимости от комплексных проводимостей фаз и нейтрального провода может находиться в любом месте внутри треугольника линейных напряжений и даже вне его, что приводит к искажению звезды фазных напряжений приемника и изменению их значений. Но если проводимость нейтрального провода бесконечно велика, то напряжение  0 и потенциал точки n, равен потенциалу точки N, а звезда фазных напряжений приемника остается симметричной при любых проводимостях фаз приемника.
2) Трехфазная цепь с несимметричным приемником

Из большого числа возможных несимметричных режимов трехфазных цепей рассмотрим только те, которые создаются приемником. При этом будем полагать, что система линейных напряжений источника питания остается симметричной и неизменной. Потенциал нейтральной точки источника питания при соединении его обмоток звездой также остается, неизменным.

Соединение фаз приемника звездой с нейтральным проводом.

^{Рассмотрим схему соединения фаз приемника, представленную на рис. 3. Сопротивление нейтрального провода, как и линейных проводов, примем равным нулю ( ).При этом условии и звезда фазных напряжений приемника остается симметричной и неизменной при любых проводимостях фаз приемника.}

Ток в нейтральном проводе определяется фазными токами.
Рассмотрим частный случай несимметричного режима, когда при симметричной активной нагрузке 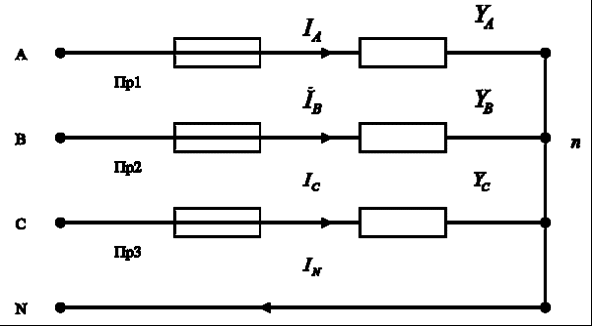происходит обрыв провода. На практике такой режим может иметь место при перегорании предохранителя Пр1.


Рис. 3. Схема соединения фаз приемника звездой с нейтральным проводом

В исходном режиме фазные токи образуют симметричную систему и ток в нейтральном проводе равен нулю. При обрыве провода А ток 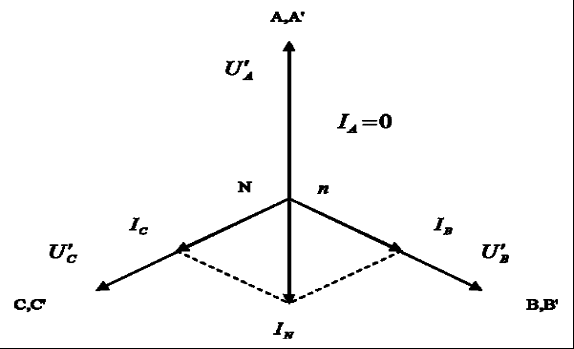. Токи в фазах В и С останутся неизменными по значению и по фазе. Ток в нейтральном проводе , т. Е. По значению равен току в исходном режиме, а по направлению противоположен ему (рис. 4).



Рис. 4 Векторная диаграмма токов при обрыве линейного провода А
(соединение приемника звездой с нейтральным проводом)

При наличии нейтрального провода фазные напряжения приемника остаются постоянными при любых нагрузках фаз и ток каждой фазы зависит только от проводимости данной фазы. Нейтральный провод, по которому протекает ток , выравнивает фазные напряжения приемника.
3) Мощность трехфазной системы

Мгновенное значение мощности отдельной фазы или, фазной мощности, определяется так же, как мощность однофазной цепи, произведением мгновенных значений фазных напряжений и тока:

(1)

При симметричной системе фазных напряжений



В общем случае несимметричной нагрузки фазные токи равны соответственно:



Подставляя в формулы (1) выражения для фазных напряжений и токов, получим значения фазной мощности для каждой фазы:



⁽²⁾



Постоянные составляющие мгновенных значений фазных мощностей, т. е. активные фазные мощности



Активная мощность трехфазного приемника равна сумме активных мощностей фаз:



При симметричной системе напряжений (U_A=U_В=U_c=U_ф) и симметричной нагрузке (I_А=I_В=I_С=I_ф; φ_А=φ_В=φ_С=φ_ф) фазные мощности равны (Р_А=Р_В=Р_С=Р_ф=U_фI_фсоsφ). Активная мощность трехфазного приемника в этом случае:

Мощность трехфазного приемника всегда удобнее вычислять через линейные напряжение и ток, так как линейные величины всегда легче измерять. Принимая во внимание, что при соединении фаз приемника звездой 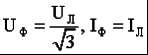, а при соединении треугольником

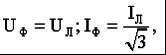( ), формула примет вид:

⁽³⁾

Эта формула справедлива как для соединения звездой, так и для соединения треугольником, но только если приемник симметричен. При этом надо помнить, что угол φ является углом сдвига фаз между фазными напряжением и током.

При симметричном приемнике его полная трехфазная мощность



а реактивная мощность:

Сумма переменных составляющих мгновенных значений фазных мощностей в уравнениях (2) при симметричном, приемнике равна нулю, так как они имеют одинаковую амплитуду и сдвинуты по фазе друг относительно друга на 2π/3. Поэтому сумма мгновенных значений фазных мощностей в этом случае равна сумме их постоянных составляющих и остается все время постоянной, равной активной мощности трехфазного приемника.