лекции по физике - 1 курс 2 семестр. Лекции по физике за второй семестр

• Название: Лекции по физике за второй семестр
• Дата: 01.06.2021
• Размер: 0.99 Mb.
• Имя файла: лекции по физике - 1 курс 2 семестр.doc
• Тип: Лекции; #212707
• страница: 2 из 6

§ 1.5. Вынужденные колебания. Переходный процесс.
Решение уравнения вынужденных колебаний, полученное в предыдущем параграфе, не зависит от начальных условий и поэтому не является единственным и общим. Это частое решение уравнения d²x/dt² + 2γ(dx/dt) + ω₀²x = (F₀/m) cosωt.

Для того чтобы найти общее решение, заметим, что сумма решений нашего уравнения x₁ = Acosωt и уравнения затухающих колебаний x₂ = A₀e^-γtcos(Ωt + φ₀) будет являться решение уравнения вынужденных колебаний. Для того чтобы в этом убедиться, подставим такое решение в уравнение x = x₁ + x₂
d²(x₁+x₂)/dt² + 2γ(d(x₁+x₂)/dt) + ω₀²(x₁+x₂) = (F₀/m) cosωt
(F₀/m) cosωt = (F₀/m) cosωt
То есть x₁ + x₂ – решение уравнения вынужденных колебаний. Мы учли, что уравнение затухающих колебаний имеет вид d²x/dt² + 2γ(dx/dt) + ω₀²x = 0.
x = Acos(ωt + φ) + A₀e^-γtcos(Ωt + φ₀)
В этом решении A, ω, φ, γ, Ω определяются параметрами системы, а величины A₀и φ₀ – произвольные и определяются из начальных условий, поэтому полученное решение является общим и единственным при заданных начальных условиях.

Рассмотрим частный случай нулевых начальных условий.
x₀ = x(0) = 0; V₀ = 0
Подставим эти начальные условия в решение: 0 = Acosφ + A₀cosφ₀

Будем считать, как в § 1.3, что затухания слабые: γ << Ω. Тогда:
dx/dt = -Aωsin(ωt + φ) - ΩA₀e^-γtsin(Ωt + φ₀) t = 0
0 = -Aωsinφ - ΩA₀sinφ₀
Получим систему уравнений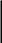




-Aωsinφ/Ω = A₀sinφ₀
-Acosφ = A₀cosφ₀
tgφ₀ = (ω/Ω) tgφ
A₀² = A²[(ω/Ω) ²sin²φ + cos²φ]
A₀ = ±A[(ω/Ω) ²sin²φ + cos²φ] ^½
Таким образом, мы нашли две произвольных величины A₀ и φ₀, которые удовлетворяют нулевым начальным условиям. Рассмотрим случай, когда ω = Ω при нулевых начальных условиях:
tgφ₀ = tgφ; φ₀ = φ; A₀ = ±A
x = Acos(ωt + φ) ± A₀e^-γtcos(ωt + φ) = A(1± e^-γt)cos(ωt + φ)
Так какx(0) = 0, то знак + не подходит. Тогда x = A(1 - e^-γt)cos(ωt + φ)

Таким образом, полученное решение состоит из двух частей. При этом вторая часть решения с течением времени уменьшается и через время релаксации практически исчезает, и, начиная с этого времени, в системе будут наблюдаться колебания, формула для которых была выведена в § 1.4.

При этом говорят, что в системе наблюдается установившийся, или стационарный процесс. Поэтому частное решение из § 1.4 часто называют стационарным решением. Это решения от начальных условий не зависит. Если t < τ, то существуют обе части решения, и в системе наблюдается переходный процесс. Форма этого процесса определяется начальными условиями. Рассмотрим случай, когда в системе нет затуханий при нулевых начальных условиях γ = 0. Тогда:
tgφ = 0; tgφ₀ = (ω/Ω)tgφ = 0; φ₀ = 0
A₀ = ±A[(ω/Ω) ²sin²φ + cos²φ] ^½ = ±A
A₀ = ±Acosωt ± A₀cosΩt
Так как x(0) = 0, то x = A[cosωt – cosΩt] = - 2A sin [(ω - Ω)t/2] sin [(ω + Ω)t/2]
Таким образом, при отсутствии затухания в системе никогда не будет наблюдаться установившееся решение. Все время происходит переходный процесс. Колебания такого вида называются биениями.
§ 1.6. Сложение гармонических колебаний двух частот
В системе с одной степенью свободы могут существовать колебания только с одной частотой. Для того чтобы в системе могли наблюдаться колебания с различной частотой, нужно много степеней свободы. Если осциллятор с двумя степенями свободы, то в нем могут наблюдаться колебания с двумя частотами. В качестве примера системы с двумя степенями свободы рассмотрим два пружинных маятника.

Пусть в положении равновесия все пружины недеформированные. Координаты каждого из грузиков будем определять по отношению к его положению равновесия. Тогда уравнения грузиков будут:
m₁(d²x₁/dt²) = -k₁x_{1 –} k₂ (x₁ – x₂)
m₂(d²x₂/dt²) = -k₃ x_{2 –} k₂ (x₂ – x₁)
Эту систему можно переписать в виде:
d²x₁/dt² = -a₁₁x₁ – a₁₂x₂ a₁₁ = (k₁ + k₂)/m₁и так далее.
d²x₂/dt² = -a₂₁x₁ – a₂₂x₂
Решение этой системы будем искать в виде:
x₁ = A₁cos(ωt + φ)
x₂ = A₂cos(ωt + φ)
Подставим в уравнение:
-ω²x₁ =-a₁₁x₁ – a₁₂x₂
-ω² x₂ =-a₂₁x₁ – a₂₂x₂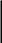




(a₁₁ - ω²) x₁ + a₁₂x₂ = 0
(a₂₂ - ω²) x₂ + a₂₁x₁ = 0

Как известно, система линейных однородных уравнений имеет нетривиальное решение, если ее определитель равен нулю.
(a₁₁- ω²)(a₂₂ - ω²) -a₂₁ a₂₁ = 0
Это условие приводит к биквадратному уравнению для ω, из четырех корней которого выбираем два положительных: ω₁ и ω₂. Тогда решение будет иметь вид:
x₁ = A₁cos(ω₁t + φ₁) + A₁cos(ω₂t + φ₁) = 2 A₁cos[(ω₁ – ω₂)t/2] cos[((ω₁ + ω₂)t/2) + φ₁]
В результате сложения двух колебаний мы получаем биение. Из математики известно, что систему однородных уравнений: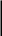
( a₁₁ - ω²) x₁ + a₁₂x₂ = 0
(a₂₂ - ω²) x₂ + a₂₁x₁ = 0
- заменой переменных x₁ =ξ₁, x₂ =ξ₂ можно привести к виду:
d² ξ₁/dt² =ω₀₁ ξ₁
d² ξ₂/dt² =ω₀₂ ξ₂
То есть система двух однородных уравнений распадается на два независимых. ξ₁ и ξ₂ – нормальные координаты системы. Такие координаты существуют всегда, но не каждый раз их легко определить. В нормальных координатах решение будет иметь вид
ξ₁ = A₀₁cos(ω₀₁t + φ₀₁)
ξ₂ = A₀₂cos(ω₀₂t + φ₀₂)
То есть каждая нормальная координата будет изменяться по гармоническому закону с одной своей собственной частотой, и никаких сложений не происходит. Таким образом, сложение гармонических колебаний будет происходить в системе с несколькими степенями свободы при условии, что эта система описывается ненормальными координатами.
§ 1.7. Физические основы анализа Фурье.
Рассмотрим систему, которая обладает n степенями свободы. Тогда одна из ненормальных координат системы будет представлять собой сумму гармонических колебаний различных частот. Для простоты выберем начало отсчета таким образом, чтобы начальные фазы всех складываемых колебаний равнялись нулю. Тогда результирующее колебание будет:
x = Acosω₁t + Acosω₂t + … + Acosω_Nt
Рассмотрим простейший случай, когда интервалы между соседними частотами одинаковы:
ω₂ – ω₁ = ω₃ - ω₂ =…= δω
∆ω = ω_N– ω₁ =δω(N-1)
Вычислим эту сумму:
x = Re [Ae^iω1t + Ae^iω2t + … + Ae^iωNt] = A[sin(Ntδω/2)/ sin(tδω/2)] Re[e^{it(ω1 + ∆ω/2)}] = A [sin(Ntδω/2)/ sin(tδω/2)] cos ω_st
ω_s= ω₁ + ∆ω/2 = (ω₁ + ω_N)/2 - средняя частота.
При сложении большого числа колебаний с различными частотами мы получили колебания с некоторой средней частотой ω_s, амплитуда которого A(t) = A зависит от времени. В этой зависимости амплитуды особой точкой будет t = 0. Для вычисления амплитуды в этой точке воспользуемся правилом Лопиталя:
A(0) = AN
A(t) = A(0) [sin(Ntδω/2)/ sin(tδω/2)]
Когда N >> 1; N → ∞; ∆ω = Nδω, апрималыхуглах sinα ≈ α.
A(t) = A(0) [sin(Ntδω/2)/ sin(tδω/2)] = A(0)[sin(tδω/2)/ (∆ωt/2)]
Таким образом, в результате сложения большого числа гармонических колебаний мы получили ограниченное во времени колебание, которое называется импульсом колебания. За длительность импульса колебания выбирают половину временного интервала между ближайшими максимуму нулями амплитуды.
∆t = t₁ = 2П/∆ω
Следует заметить, что справедливо и обратное утверждение. Любой произвольный импульс колебания x(t) можно представить в виде суммы гармонических колебаний с различной амплитудой и частотой. Такое представление называется анализом Фурье:
x(t) = ∫ A(ω)cos(ωt + φ(ω))dω
Зависимость амплитуды складываемых колебаний A(ω) от ω– спектр колебания.

В рассмотренном примере мы получили соотношение между длительностью импульса и шириной спектра колебаний. Так как был выбран простейший частный случай, то мы получили и частное решение.

Глава 2. Волны.
§2.1. Волновой процесс. Волновая функция.
Волновым процессом, или волной будем называть любое различимое возмущение, распространяющиеся в пространстве. При этом форма возмущения может меняться, но оно всегда должно оставаться различимо.

Волновые процессы описываются различными уравнениями. Мы рассмотрим лишь одно из них.
, где

- волновая функция




Рассматриваемое уравнением является дифференциальное уравнение частной производной второго порядка.

Рассмотрим двумерный случай, когда



Решение дифференциального уравнения будем искать в виде функции

Полученное решение представляет собой возмущение, распространяющиеся вдоль оси X со скоростью .

Точно так, это возмущение, распространяющееся в противоположную сторону.

Общее решение уравнения будет

Рассмотрим трехмерный случай

Рассмотрим сферически симметричное решение

В этом случае волновое уравнение удобно переписать из координат в переменную






Точно также










Тогда уравнение будет иметь вид:

Получаем одномерное волновое уравнение, решение которого уже найдено



Решение представляет собой возмущение, сделанное в точке =0 и уменьшающееся по величине при распространении бесконечности.

Решение описывает возмущение, которое возникает из ничего на бесконечности и растет при приближении к нулю (центру). Такое решение физически невозможно.

Поэтому в сферически симметричном случае , где - произвольная функция.