лекции по физике - 1 курс 2 семестр. Лекции по физике за второй семестр

• Название: Лекции по физике за второй семестр
• Дата: 01.06.2021
• Размер: 0.99 Mb.
• Имя файла: лекции по физике - 1 курс 2 семестр.doc
• Тип: Лекции; #212707
• страница: 4 из 6

§2.5. Многолучевая интерференция

Рассмотрим излучают сферические волны с одинаковой амплитудой, частотой и одинаковой . Расстояние между источниками так же одинаково.

Определим волновую функцию , находящуюся в волновой зоне:









где

,
То есть в точке мы будем наблюдать волновую функцию, амплитуда которой:

Рассмотрим случай, когда

Вычисляя предел этой функции по Лопиталю, находим, что

Точно так же, мы можем определить амплитуду волновой функции, когда

,





При таких углах будут наблюдаться максимумы амплитуды, которые называются главными.

Если , где , кроме кратных

- условие минимума

,
Получаем побочные максимумы.

Следует заметить, что амплитуда побочных максимумов неодинакова в отличие от главных.
§2.6. Дифракция. Признак Гюйгенса
Рассмотрим точечный источник излучения , от которого распространяются сферические волны, и который находится на большом расстоянии от экрана с отверстием. Величина отверстия . Определим волновую функцию точки , которая также находится на большом расстоянии от экрана, но с другой стороны.

Гюйгенс предположил, что волновая функция в точке , будет складываться из волновой функции источника и волновой функции от экрана :

Если отверстие в экране закрыто пробкой, то волновая функция в точке будет складываться из волновой функции от источника и волновой функции от экрана с отверстием:

В результате сложения волновых функций в точке волновая функция будет равна нулю.

Волновая функция в точке будет с точностью до знака совпадать с волновой функцией, излучаемой только пробкой. Каждую точку волнового фронта в отверстии экрана рассматривать как источник вторичных волн. Волновая функция в точке будет равна сумме вторичных волн.

Для того чтобы определить волновую функцию в точке , заметим, что волновой фронт в отверстии экрана можно считать плоским, так как источник находится на очень большом расстоянии от него. Разобьем поверхность волнового фронта на точечные источники излучения. Каждый источник излучает сферическую волну с одинаковой амплитудой, частотой и одинаковой начальной фазой, которую будем считать равной нулю. Так как точка находится в волновой зоне, то можно допустить, что амплитуды волновых функций от каждого источника одинаковы.


Для того чтобы определить амплитуду волновой функции:
,
Получим

Тогда


При рассмотрении открытой части волнового фронта мы предположили, что источников очень много:







Получим:


Амплитуда будет равна нулю, если



- условие минимума
Если , , то мы получим условие максимума

Полученный пучок излучения принято характеризовать угловой шириной, или расходимостью пучка . За величину выбирается половина расстояния между ближайшими к нулю нулями амплитуды.






Размер изображения отверстия на экране будет будет значительно превышать геометрическое изображение отверстия. Проникновение изображение в область геометрической тени называется дифракцией.
§2.7. Дифракционная решетка
Рассмотрим экран, в котором проделано отверстий (щелей). Ширина каждого из них . Такой экран называется дифракционной решеткой.

Пусть источник излучения находится на большом расстоянии от решетки. Определить волновую функцию в точке , лежащей в волновой зоне с другой стороны решетки. Волновая функция в точке будет равна сумме волновых функций от каждого отверстия решетки. То есть

Повторяя выводы §2.5. находим, что это будет равняться

При определении волновой функции в точке


необходимо учесть, что каждый источник имеет конченые размеры и не является точечным, как было §2.5. Для определения амплитуды излучения такого источника надо воспользоваться результатом §2.6., где была получена амплитуда



Положение главных максимумов определяется условием , и зависит от длины волны излучения , за исключением центральной.

Это свойство дифракционной решетки позволяет определить спектральный состав излучения. То есть если источник испускает волны с различной длиной, с помощью дифракционной решетки можно найти длины этих волн, так как условие главного максимума кроме центрального, будет _, и волны различной длины будут наблюдаться под разными узлами .

Максимумы первого порядка будут определять спектр первого порядка излучения.

Релей предложил критерий различимости двух линий в спектре излучений, если главный максимум одной длины волны совпадает с ближайшим минимумом другой. .







- минимальный интервал длин волн, который можно разрешить с помощью дифракционной решетки.



- разрешительная способность, или ее разрешение
§2.8. Принцип Гюйгенса – Френеля. Дифракция Френеля
Если источник находится на большом расстоянии от экрана с отверстием, а точка наблюдения также находится на большом расстоянии от экрана, то наблюдаемая дифракция называется дифракцией Фраунгофера. Если нарушается хотя бы одно из этих условий, то дифракция называется дифракцией Френеля.

Френель дополнил принцип Гюйгенса следующим условием. Для того чтобы найти волновую функцию в точке , надо разбить поверхность волнового фронта на бесконечно малые плоские участки. Тогда волновая функция в точке будет равна сумме волновых функций, излучаемых каждым таким участком поверхности, что совпадает с принципом Гюйгенса. Амплитуда волн, излучаемая каждым участком поверхности, будет , где - амплитуда колебаний на поверхности волнового фронта.

- некоторая функция, зависящая от угла между нормалью и радиус вектором, про которую известно только то, что она уменьшается с увеличением угла.
Рассмотрим цилиндрически-симметричную задачу, когда источник – центр отверстия в экране, и точка находятся на одной прямой. Источник находится на большом расстоянии от поверхности, тогда волновой фронт в отверстии экрана можно считать плоским. По признаку Френеля волновая функция в точке будет равна сумме волновых функций, излучаемых небольшими участками волнового фронта.


Тогда амплитуда колебаний:

Тогда амплитуда колебаний:


В качестве бесконечно малого участка поверхности 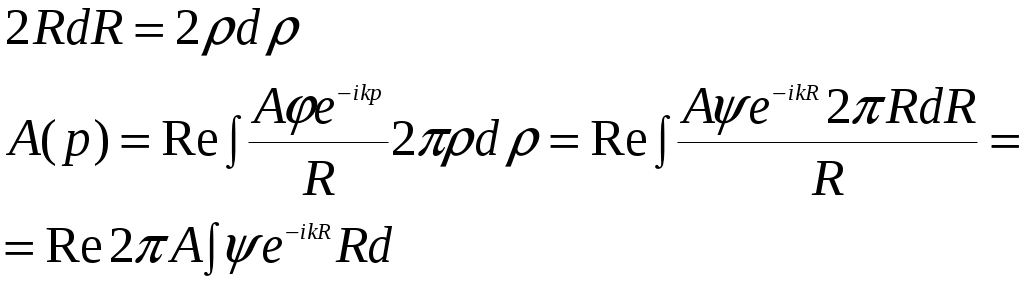, выберем тонкое кольцо радиусом



Таким образом, амплитуда колебаний в точке будет пропорциональна реальной части интеграла.

Для вычисления этого интеграла предположили сначала, что функция постоянна:





Таким образом, если предположить, что , то интеграл не сходится. Влияние функции приведет к тому, что каждое следующее слагаемое будет меньше предыдущего, и в результате окружность деформируется в спираль Френеля. Если отверстие в экране бесконечно большое, то амплитуда колебаний в точке будет определяться радиусом окружности.

Френель предложил разбить поверхность волнового фронта на зоны (зоны Френеля) таким образом, что расстояние до границы от точки отличается на .

Легко заметить, что первой зоне Френеля соответствует первая полуокружность спирали, вторая зона Френеля – вторая полуокружность спирали и т.д.

Если отверстие в экране совпадает с размером первой зоны Френеля, то амплитуда в отверстии экрана будет равняться , а энергия при этом будет в 4 раза больше.

Рассмотрим радиус n-oй зоны Френеля

Рассмотрим случай, когда точка наблюдения находится на очень большом расстоянии от экрана с отверстием, и будет очень много больше размера отверстия.

То есть, в отверстие экрана попадает малая часть первой зоны Френеля, поэтому амплитуда колебания точки будет небольшой.

Если точка P будет приближаться к экрану, то радиус первой зоны Френеля будет уменьшаться, и в отверстие будет попадать все большая ее часть, то есть амплитуда будет увеличиваться. Максимальная амплитуда будет тогда, когда радиус первой зоны Френеля совпадет с размером отверстия. При дальнейшем приближении в отверстии будет уменьшаться вторая зона Френеля, и амплитуда будет убывать. Когда в отверстии экрана уместятся обе зоны Френеля, амплитуда колебаний практически будет равна нулю.
§2.9. Волновой пакет
Рассмотрим две монохроматические волны, которые распространяются вдоль оси х с разной частотой и разным волновым вектором.
f₁ = Acos(ω₁t - k₁x)
f₂ = Acos(ω₂t – k₂x)
f(x,t) = 2Acos(ω_mt – k_mx)cos(ω_st – k_sx)
В следующий момент времени вся картина сместится вдоль оси х, причем с разной скоростью будут перемещаться огибающая и наполняющая.

Для определения скорости огибающей надо продифференцировать условие постоянства фазы:

ω_m – k_m(dx/dt) = 0
dx/dt = ω_m/k_m
Точно так же можно найти скорость наполняющей, причем эти скорости могут не совпадать. Рассмотрим большое количество монохроматических плоских волн с различной частотой и волновым вектором, которые распространяются вдоль оси х. Пусть интервал между соседними частотами будет одинаковым:
ω₁ – ω₂ = ω₂ – ω₃ =…= δω
∆ω = ω_N– ω₁ =δω(N-1)
Пусть интервал между соседними волновыми числами тоже одинаков:

Δk = k₂ – k₁ = k₃ - k₂
Это возможно только в одном случае: когда нет дисперсии, то есть фазовая скорость постоянна.
Vp = ω/k = const
Тогда волновая функция будет:
f(x,t) = Acos(ω₁t – k₁x) + Фcos(ω₂t – k₂x) +… = A₀[sin((∆ωt - ∆kx)/2)/(∆ωt - ∆kx)/2] cos( ωst - ksx)
Мы получили волновую функцию, амплитуда которой будет зависеть от времени и координат.
∆kx₁ = 2П
Таким образом, при сложении большого числа монохроматических волн с различной частотой мы получили волновую функцию, ограниченную в пространстве. Такая функция – волновой пакет. За протяженность волнового пакета выбирается половина расстояния между ближайшими максимуму нулями. Протяженность волнового пакета и интервал волновых чисел, образующих его монохроматических волн, связаны между собой соотношением:
∆k∆x = 2П
Следует заметить, что это равенство получено при определенных условиях.

Любой волновой пакет можно представить в виде суммы монохроматических волн:
f(x,t) = ∫A(k)cos(W(k)t – kx)dk
ω = W(k) – дисперсионное соотношение
Рассмотрим поведение волнового пакета в следующие моменты времени. В следующий момент времени t > t = 0 все складываемые волновые функции сместятся вдоль оси х на одинаковое расстояние, так как в отсутствии дисперсии скорости одинаковы. В результате сумма этих волновых функций тоже сместится на то же расстояние.

Скорость перемещения волнового пакета будет совпадать с фазовой скоростью волн, при этом очевидно, что форма волн пакета неизменна.

Если фазовые скорости различны для разных волн (есть дисперсия), то волновой пакет будет деформирован при распространении, и скорость его движения будет отлична от фазовой скорости волны.


§2.10. Групповая скорость. Метода стационарных фаз.
В §2.9 было показано, что любую произвольную волновую функцию (волновой пакет) можно представить в виде суммы гармонических волн.
f(x,t) = ∫A(k)cos(W(k)t – kx)dk = ∫A(k)cosθ(k)dk
θ(k) = W(k)t – kx - фаза гармонической волны.
Заметим, что вычисление интеграла в общем виде – очень сложная задача. Заметим так же, что при сложении гармонических функций результат будет заметно отличаться от нуля, только если фазы гармонических колебаний будут близкими. Во всех остальных местах результат будет близок к нулю, то есть условие того, что полученный интеграл не равен нулю, совпадает с условием одинаковой степени фаз складываемы волн, то есть с условием постоянства фазы для различных k.
dθ/dt = 0
θ = W(t)t – kx
(dW/dk)t – x = 0
В точках х = (dW/dk)t интеграл будет отличен от нуля. В этих точках будет находиться волновой пакет. То есть волновой пакет будет перемещаться со скоростью:

V_g= dW/dk = dω/dk, где эта величина называется групповой скоростью.
W(k) = ω, так как V_p = ω/k
ω = V_pk
V_g= dω/dk = V_p + k(dV_p/dk)
Если фазовая скорость V_p не зависит от k (иными словами, нет дисперсии), то групповая скорость совпадает с фазовой. В противном случае групповая скорость будет отличаться от фазовой. Таким образом, рассматриваемы интеграл будет отличаться от нуля лишь небольшой области значений k, для которых фаза волны θ(k) примерно одинакова. Для того чтобы найти это значение k, надо решить полученное ранее уравнение относительно k, из которого найдем корень k₀ = k(x,t). Тогда
f(x,t) = ∫A(k)cosθ(k)dk = 2εA(k₀)cosθ(k₀) = A(x,t)cos[ω(x,t)t – k(x,t)x]
Любой произвольный волновой пакет можно записать в том же виде, что и монохроматическую волну с той лишь разницей, что амплитуда, частота и волновой вектор зависят от координат и времени.

Для произвольной волновой функции f(x,t) = ∫A(x,t)cosθ(x,t) можно ввести понятие частота ω и волновой вектор k.
Частота волновой функции: ω = ∂θ/∂t
Волновой вектор: k = - ∂θ/∂x

§2.11. Пространственная и временная когерентность. Поляризация.
§2.4 было показано, что условие максимума интерференции двух источников сводится к тому, что геометрическая разность хода S = dsinθ = mλ, то есть целому числу длин волн. d– расстояние между источниками. Угловое расстояние между двумя ближайшими максимума ∆θ = θ₂ – θ₁.
d(sinθ₂ – sinθ₁) = λ
Для малых углов sinθ₁ ≈θ₁

sinθ₂ ≈θ₂
d(θ₂ – θ₁) = λ
∆θ = λ/d
Если источники излучаемы волн с различное длиной волн, то положение максимума будет размыто, так как условия максимума dsinθ = mλ для размытых длин волн будет выполняться для разных углов. Если источники излучают волны в интервале от λ₂ – λ₁ = δλ, то при малых углах условие максимума будет:
dθ = mλ
dδθ = mδλ, где δθ – угол размытия максимума.
Для того чтобы картина интерференции наблюдалась, необходимо, чтобы ∆θ > δθ.
∆θ = λ/d > mδλ/d
m < λ/δλ
Тогда геометрическая разность хода:
S = mλ < λ²/δλ
λ²/δλ – длина когерентности.
Для того чтобы наблюдалась интерференционная картина, необходимо, чтобы разность хода была больше длины когерентности. Выясним, что такое λ²/δλ.

В §2.9 было показано, что размытость волнового пакета ∆x удовлетворяет соотношению ∆x∆k = 2П, где ∆k = 2П[(λ₁ – λ₂)/( λ₂ – λ₁)] = 2П(δλ/λ²)
∆x = λ²/δλ
То есть длина когерентности совпадает с длиной волнового пакета.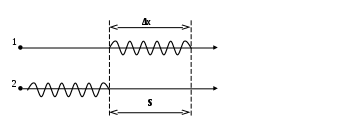


Если два источника излучают волновые пакеты, то в точке наблюдения Р мы будем регистрировать импульсы колебания. Если время регистрации будет меньше длительности импульса колебания, то колебания будут складываться.

Длительность импульса колебаний ∆t – время когерентности.
∆t∆ω ≈ 2П
∆t ≈ 2П/∆ω
Таким образом, если время, в течение которого происходит регистрация волновых функций, меньше времени когерентности, а расстояние, на котором наблюдается волновая функция меньше длины когерентности, то источники этой функции когерентны.

Волновая функция, как правило, описывает физические величины и, так же как и они, может быть скалярной и векторной.

Если волновая функция векторная, то существует три класса волн:

1. 
   поперечные
   
2. 
   продольные
   
3. 
   косые
   

В случае поперечных волн вводят понятие поляризации волн. Это понятие характеризует поведение вектора волновой функции, если при распространении волны вектор волновой функции все время остается в одной плоскости, то говорят, что волна плоска, или линейно поляризована.

Если при распространении волны величина волнового вектора постоянна, а направление меняется по кругу, то говорят о круговой поляризации волн.

Если при этом еще меняется и величина волнового вектора, то говорят об эллиптической поляризации волнового вектора.

Следует заметить, что при такой классификации любая поперечная векторная волна будет поляризована.

Реальные источники волн обычно излучают волновые пакеты, каждый из которых поляризован по-своему. Если время регистрации будет больше времени когерентности, то поляризацию каждого волнового пакета определить не удастся, и в этом случае говорят об естественной, или неполяризованной волне. То же самое будет, если расстояние, на которой наблюдаются волны, будет больше длины когерентности.

§2.12. Приближение геометрической оптики. Уравнение Эйконала. Принцип Ферма.
В §2.10 было показано, что любую произвольную волновую функцию можно записать в виде:
f(R,t) = A(R,t)cos(θ(R,t)), где θ(R,t) – фаза волны.
Поверхность, в каждой точке которой θ(R,t) одинакова, называется волновой поверхностью. В общем случае она может быть произвольной.




Разобьем эту поверхность на такие участки, что им можно считать плоскими. Если при этом размер участка будет много больше длины волны, а время, в течение которого этот участок остается плоским много больше периода волны, то можно говорить о приближении геометрической оптики.

Рассмотрим один такой участок. Для простоты начало координат поместим на этот участок и за начало отсчета времени выберем нуль. Разложим фазу колебаний в степенной ряд.

θ(R,t) = θ(0) + t(∂θ/∂t)(0) + x(∂θ/∂x) + y(∂θ/∂y) + z(∂θ/∂z) +... + = θ(0) + t(∂θ/∂t) + RΔθ + ... = θ(0) + ωt – kR + ...
В приближении геометрической оптики рассматриваемый участок волнового фронта можно считать частью плоской волны, для которой фаза волны ωt – kR, а фазовая скорость V_p = ω/R.

В приближении геометрической оптики при разложении в ряд фазы можно ограничиться лишь первыми членами ряда.
θ(R,t) = θ(0) + ωt – kR
В этом приближении можно считать, что направление распространения произвольной волны совпадает с направлением вектора k в каждой точке волнового фронта, а скорость распространения фазы будет:
V_p² = (ω/∆θ)² - уравнение Эйконала.
Луч – линия, касательной к каждой точке которой является вектор k.

Для определения формы луча очень полезен принцип Ферма, для вывода которого рассмотрим разность фаз ∆θ в двух точках пространства, расположенных на одном луче в один и тот же момент времени. Эту разность фаз можно вычислить, интегрируя бесконечно малые изменения фазы вдоль луча.
∆θ = ∫dθ
dθ = (∂θ/∂t)dt + ∆θdR
Так как время постоянно, dt = 0, ∆θ = ∫∆θdR
С другой стороны dR = dl
Градиент θ = -k → ∆θ = -k направлен по касательной к траектории, как и dl.
∆θdR = ∆θdl = |∆θ||dl|
Из уравнения Эйконала: V_p = ω/|∆θ|; |∆θ| = ω/V_p
∆θ = ∫ωdl/V_p = ω∫dl/V_p
Этот интеграл вычисляется вдоль луча и равен времени распространения волны вдоль луча. Заметим, что разность фаз – величина постоянная и не зависит от способа нахождения. Ту же самую разность можно вычислить по другой траектории, не совпадающей с лучом, но в этом случае полученный результат будет неверен, так как ∆θ и dl не параллельны.

Выбирая каждый раз другую траекторию, не совпадающую с лучом, мы будем получать различные результаты, то есть ∆θ будет зависеть от траектории, и только в одном случае, когда эта траектория совпадает с лучом, ∆θ не зависит от формы траектории.

Условие независимости функции и условие ее экстремума совпадают, поэтому интеграл, вычисляемый вдоль луча, не зависит от формы луча и является экстремальным. Оказывается, что на траектории луча это минимальная величина.

Время распространения волны вдоль луча минимально.
∫dl/V_p = min - принцип Ферма.
§2.13. Электромагнитные волны в вакууме.
Электромагнитное поле полностью описывается уравнениями Максвелла, которые в вакууме будут иметь вид:

(∆ считать ротором. Буквы, выделенные жирным курсивом – векторными величинами)
∆E = 0; ∆B = 0
∆×E = -(∂B/∂t); ∆×B = (1/c²)(∂E/∂t);
∆×(∆×B) = ∆×[(1/c²)(∂E/∂t)]
∆(∆B) - B(∆∆) = ∆(∆B) - ∆²B =(1/c²)(∂/∂t)(∆×E)
- ∆²B = (1/c²)(∂ ²B/∂t²)
(∂ ²B/∂t²) - c²∆²B= 0

Уравнение для B совпадает с волновым уравнением, решение которого было найдено в §2.1. Точно так же можно вычислить:
∆×(∆×E) = ∆×(∂B/∂t)
∆(∆E) - ∆²E =-(∂/∂t)(∆×B)
- ∆²E = (1/c²)(∂ ²E/∂t²)
(∂ ²E/∂t²) - c²∆²E= 0
То есть и для электрического поля м ыполучаем волновое уравнение. Таким образом, решения уравнения Максвелла в вакууме будут иметь вид волновых функций. ЖДля простоты рассматриваем сначала случай гармонических волн.

E=E₀e^{i(ωt - kR)}
B=B₀e^{i(ωt - kR)}
Т 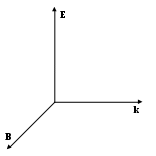о есть мы ищем решение уравнения максвелла в виде плоских монохроматических волн. Подставим решение в уравнение Максвелла, при этом учтем, что ∆ можно заменить на ∂/∂R.
∆E= 0 → - ikE= 0→ k перпендикулярен E.
∆B= 0 → ikB= 0→ k перпендикулярен B.
∆×E = -(∂B/∂t)
- ik×E = - iωB
k×E = - ωB
k×B = (1/c²)(∂E/∂t)
- ik×B = (i/c²)ωE
k×B = (ω/c²) E
kE = ωB
E = ωB/k
E = cB

§2.14. Энергия электромагнитного поля. Вектор Умова-Пойнтинга.
Рассмотрим некоторый замкнутый объем, ограниченный поверхностью S, в котором существует электромагнитное поле. Предположим, что это поле обладает энергией, плотность которой u. Тогда полная энергия электромагнитного поля будет ∫udV.

Вычислим скорость изменения энергии: (∂/∂t) ∫udV.

Изменение энергии в объеме V может происходить по двум причинам:

1. 
   за счет переноса энергии
   
2. 
   за счет мощности всех сил, действующих в системе
   

Для вычисления энергии, переносимой через поверхность S, введем вектор uV, где V – скорость переноса энергии, который называется вектором плотности потока энергии. Тогда энергия, переносимая в единицу времени через поверхность площадью dS, будет uVdS.

Так как это будет энергия, выносимая из объема, то за единицу времени энергия в объеме уменьшается на величину -∫uVdS (по замкнутой поверхности).

Если внутри объема V имеются электрические заряды, то электрическое поле будет совершать работу, что приведет к уменьшению энергии поля (работа магнитного поля равна нулю). Как мы знаем, мощность электрических сил в единице объема будет jE, поэтому за единицу времени энергия электромагнитного поля в объеме V уменьшится на величину -∫jEdV, тогда
∫(∂u/∂t)dV = -∫(по замк. объему)uVdS - ∫jEdV

∫(∂u/∂t)dV + ∫∆(uV)dV = - ∫jEdV, так как это равенство должно быть выполнено для любого объема V, то
(∂u/∂t) + ∆(uV)= - jE
Рассмотрим уравнение Максвелла в среде:
∆E = ρ/ε₀
∆B = 0
∆×E = -(∂B/∂t)
∆×B = (j/ε₀c²) + (1/c²) (∂E/∂t)
- jE = (ε₀(∂E/∂t) - ε₀c²∆×B) E
Рассмотрим ∆(E ×B)
∆(E ×B) = ∆_ε(E ×B) + ∆_B(E ×B) = B(∆×E) – E(∆×B)
-jE = 0,5ε₀(∂E/∂t)² + ε₀c² (∆(E ×B) – B(∆×E)) = (∂E/∂t) (0,5ε₀E² + 0,5ε₀c²B²) + + ε₀c²∆(E ×B) = (∂u/∂t) + ∆(uV)
Сравнивая полученные выражения, находим, что плотность энергии электромагнитного поля будет:
u = 0,5ε₀E² + 0,5ε₀c²B²
Вектор плотности потока:
S = ε₀c² E×B - вектор Умова-Пойнтинга
Чтобы убедиться, что полученные результаты верны, вспомним §2.13:
BC = E; u = ε₀E²
S = ε₀c² E×B = ε₀c|E×B|V_p = ε₀E²V_p = uV_p
|V_p| = с
Таким образом, электромагнитное поле облагает энергией, плотность которой будет:
u = 0,5ε₀E² + 0,5ε₀c²B²