|
|
лекции по физике - 1 курс 2 семестр. Лекции по физике за второй семестр
Часть IV. Квантовая механика.
§ 1. Экспериментальные основы квантовой механики.
К началу XX века основные физические явления были объяснены классической физикой, за исключением нескольких явлений:
1). Тепловое излучение тела
Как известно, любая движущаяся с ускорением частица излучает электромагнитные волны. Так как все тела содержат заряженные частицы, то при температуре выше абсолютного нуля они двигаются с ускорением, поэтому любое тело при температуре выше абсолютного нуля излучает электромагнитные волны, частота которых (0;∞)
Пусть энергия излучения электромагнитных волн за единицу времени на единицу поверхности в интервале (ω;dω) будет I(ω)dω. Величина I(ω) – спектральная плотность излучения. С помощью классической электродинамики Максвелла можно получить эту зависимость:
I(ω) ω² - Закон Джинса-Релея, или ультрафиолетовая катастрофа.
2). Фотоэффект
В начале XX века было открыто явление фотоэффект, которое заключается в том, что электромагнитная волна вырывала с поверхности проводника электроны. Само это явление легко объяснить классической электродинамикой. Под действием электрического поля волны электроны проводника начинают двигаться вдоль поверхности, а на движущийся электрон будет действовать сила qV×B со стороны магнитного поля, которое направленно наружу, а следовательно приводит к вырыванию электронов. Столетов экспериментально установил, что с увеличением амплитуды волны скорость вылета электроном не меняется, а меняется только их число, что невозможно объяснить классической физикой.
3). Опыты по дифракции электронов
1. Опыт с пулями.
Имеем: пулемет, пуленепробиваемый заслон и двумя отверстиями и мишень позади заслона. Будем описывать попадание пуль в мишень вероятностью попадания Р. Вероятности складываются.
2.Опыт с волнами.
Имеем: источник излучения, заслон с двумя отверстиями, не пропускающий волны и экран позади заслона. Будем описывать квадратом амплитуд. Если открыто одно отверстие, то будем наблюдать явление дифракции. Если же открыть оба отверстия, имеет место интерференция.
3. Опыт с электронами.
Имеем: электронную пушку, электрононепробиваемый заслон с двумя отверстиями и мишень позади заслона. Характеризуем вероятностью попадания в мишень, а вероятности не складываются, а интерферируются. Как только мы начинаем следить за электроном, вылетающим в дырочку, получается сложение, а как только перестаем следить – интерференция. Возникает вопрос: электрон имеет интеллект?
Вывод: электроны описываются вероятностью, как и пули, а вероятности интерферируются, как у волн.
§ 2. Волны де Бройля.
Так как электроны проявляют одновременно волновые и корпускулярные свойства, то возникла идея, что этим обладают и все остальные частицы и поэтому общие законы механики частиц и волн должны совпадать. В теории волн общим законом является принцип Ферма, который позволяет определить траекторию луча из условия минимума интеграла.
∫ dl/Vp= min
Оказывается, что такой же принцип существует и в классической механике.
∫(E-u)1/2 dl = min,
где Е – полная энергия
u – потенциальная энергия
Очевидно, что при объединении свойств траекторий луча и частицы, луч и частица – одно и то же. Эти принципы должны выполняться одновременно.
1/Vp= α (E-u)1/2
где α – коэффициент пропорциональности
С другой стороны скорость частицы: V = [2(E-u)/m] 1/2 - должна соответствовать групповой скорости волн Vg = dω/dk
1/V = 1/Vg = [m/2(E-u)] 1/2 = dk/dω
Vg = ω/k
k = αω(E-u)1/2
[m/2(E-u)] 1/2 = (E-u) 1/2 (d(αω) /dω) + dE(2(E-u)1/2)
Так как это равенство должно выполняться при любой полной энергии Е частиц и любой потенциальной энергии u, то коэффициент (E-u) в первой и правой частях равны.
d(αω) /dω = 0
(m/2)1/2 = (dω/2)(dE/ dω)
dω = const; dE/ dω – постоянная Планка
ħ = h/2П
E = hω + E0
Интегрируя, получаем, что E = ħω + E0, где E0 = произвольная const, так как, если частицы нет, ее полная энергия равна нулю, то частота волны равно нулю и E0 = 0.
E = ħω
(m/2)1/2 = αħω/2
α = (2m)1/2/ħm
1/Vp = α(E-u)1/2 = k/ω = (αm(E-u)) 1/2 / ħω
ħk = P
P = mV – импульс частицы
Таким образом, частица с одной стороны характеризуемся корпускулярными характеристиками (E и P), а с другой стороны – волновыми (ω и k), которые связаны между собой соотношениями:
k = 2П/λ
h/λ = P
λ = h/P - длина волны де Бройля
Таким образом, каждой частице соответствует некоторая волновая функция:
ψ(R,t) = Aei(kR- ωt)
Полученная волновая функция называется волной де Бройля, или волновой функцией частиц.
§ 3. Уравнение Шредингера.
Как было показано в § 2.1, волновая функция – это решение волнового уравнения, поэтому для волновой функции де Бройля мы можем написать точно такое же уравнение, как в § 2.1:
∂2ψ/∂t2 – Vp2Δ2ψ = 0
Рассмотрим волновую функцию в виде монохроматической волны, то есть с ω = const, которая в нашем случае будет ω = E/t. Тогда волновую функцию можно представить в виде:
φ(R,t) = Aei(kR- ωt) = φ(R)e-iωt
Подставим функцию в уравнение
-ω2φ(R)e-iωt - Vp2e-iωtΔ2φ(R) = 0
-ω2φ(R) - Vp2 Δ2φ(R) = 0
Vp2 = ω/k = ħ2ω2/p2 = ħ2ω2/2m(E-u)
ω2φ + ħ2ω2/2m(E-u)
(ħ2/2m) Δ2φ(R) + (E-u) φ(R) = 0
Это уравнение Шредингера для независящей от времени части волновой функции частицы φ(R) и часто называется стационарным уравнением Шредингера.
Умножим это уравнение на e-iωt
(ħ2/2m) Δ2 ψ(R,t) + E ψ(R,t) – uψ(R,t) = 0, где ψ(R,t) = φ(R)e-iωt
∂ψ/∂t = -iωψ = (-iE/ħ)ψ
Eφ = iħ(∂ψ/∂t)
iħ(∂ψ/∂t) + (ħ2/2m) Δ2 ψ – uψ = 0
Полученное уравнение называется уравнением Шредингера. Рассмотрим комплексно-сопряженное уравнение Шредингера.

iħ(∂ψ/∂t) + (ħ2/2m) Δ2 ψ – uψ = 0
-iħ(∂ψ*/∂t) + (ħ2/2m) Δ2 ψ* – uψ* = 0
iħ(ψ*(∂ψ/∂t) + ψ(∂ψ*/∂t)) + (ħ2/2m)(ψ*Δ2ψ - ψΔ2 ψ*) = 0
iħ(∂ψ/∂t)(ψψ*) + (ħ2/2m) Δ(ψ*Δψ - ψΔψ*) = 0
Δ(ψ*Δψ - ψΔψ*) = Δψ*Δψ + ψ*Δ2ψ – ψΔψ* - ψΔ2ψ*
Тогда уравнение (∂ψ/∂t)(ψψ*) + (ħ2/2mi) Δ(ψ*Δψ - ψΔψ*) = 0 по внешнему виду напоминает уравнение непрерывности. Чтобы убедиться в этом, рассмотрим волновую функцию в виде плоской монохроматической волны:
φ = Aei(kR- ωt) = F(t)eikR
Подставим
(ħ/2mi) Δ(ψ*Δψ - ψΔψ*) = (ħ/2mi) Δ(F* e-ikR - FikeikR – FF*e-ikR (-k)) = (ħ/2mi)Δ(2kψψ*) = Δ((ħk/m) ψψ*) = Δ(V ψψ*)
ħk = P = mV
То есть полученное уравнение действительно совпадает с уравнением непрерывности, где вместо ρ надо ставить ψψ* = |ψ|2, а V – скорость частицы. Уравнение непрерывности выполняется для любой величины, где ρ – плотность заряда или вещества (материи). Такую же роль в квантовой механике играет ψ.
Квадрат модуля волновой функции ψψ* = |ψ|2 можно рассматривать, как плотность вероятности обнаружить частицу в интервале R ÷ R+dR. Вследствие этого волновая функция обладает таким свойством:
* Условие нормировки ∫|ψ|2dR = 1, для выполнения которого необходимо, чтобы
ψ(R)=>0; R =>±∞ и волновая функция и ее производные должны быть непрерывны.
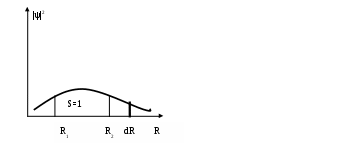
§ 4. Принцип неопределенности Гейзенберга.
Рассмотрим одномерный случай, когда волновая функция частицы ψ(R,t) = ψ(x,t). Если волновая функция частицы представляет собой волновой пакет, протяженностью ∆х, то очевидно, что вероятность обнаружить частицу будет отлична от нуля только там, где существует волновой пакет. Таким образом, о местоположении частицы можно говорить лишь с некоторой определенностью ∆х, для определения которой вспомним § 2.9:
∆х∆k ≥ 2П
∆х∆ħk ≥ 2Пħ
∆х∆P ≥ 2Пħ, где ∆х – неопределенность координаты частицы
∆P – неопределенность ее импульса
∆х∆P ≥ 2Пħ - Первое соотношение неопределенностей Гейзенберга для координаты и импульса.
Отсюда следует, что, при условии известности координаты частицы, мы не знаем ее импульса. Если мы находимся в некоторой точке, и мимо нас пролетает частица, то есть мимо нас распространяется волновой пакет, то мы будем наблюдать импульс колебаний длительностью ∆t. Эта ∆t определяет неопределенность времени, когда частица находится в данной точке в пространстве. То есть частица находилась в данной точке пространства с разной вероятностью в течение интервала времени.
В § 1.7 было показано, что ∆t∆ω ≥ 2П
∆t∆(ωħ) ≥ 2Пħ
∆t∆E ≥ 2Пħ - Второе соотношение Гейзенберга для энергии и времени
Таким образом, если мы знаем энергию, не знаем времени, знаем время – не знаем энергии.
§ 5. Движение частицы в поле с потенциальным барьером. Туннельный эффект.
Рассмотрим одномерный случай. Пусть потенциальная энергия частицы имеет форму барьера.
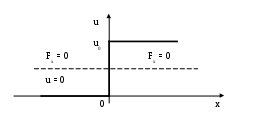
Fx = - (∂u/∂x)
Рассмотрим частицу, полная энергия которой Е < u0. Для определения волновой функции при заданной энергии Е = ħω достаточно рассматривать стационарное уравнение Шредингера, из которого находим φ(x).
ψ(x,t) = φ(x)e-iωt
ω = E/ħ
В одномерном случае
(ħ2/2m)(d2φ/dx2) + (E-u)φ = 0
Рассмотрим область x<0, u=0, тогда
(ħ2/2m)(d2φ/dx2) + Eφ = 0
Как известно, решение этого уравнения будет иметь вид:
φ(x) = Ae±ikx
(ħ2/2m)(-k2) Ae±ikx+ EAe±ikx = 0
k = (2mE/ ħ2) ½
Общее решение можно представить в виде:
φ(x) = Aeikx+ Be-ikx
ψ(x,t) = φ(x)e-iωt= Ae±ikx+ EAe±ikx
Таким образом, в полученном решении у нас будет две волновые функции:
1) распространяющаяся вдоль оси х (падающая волна)
2) распространяющаяся в противоположном направлении (отраженная волна)
|A|2 определяет плотность вероятности обнаружить частицу, которая двигается к потенциальному барьеру.
|В|2 определяет плотность вероятности обнаружить отраженную частицу.
k = |B/A|2 - коэффициент отражения
Рассмотрим x > 0, u = u0 > E
(ħ2/2m)(d2φ/dx2) + (E - u0)φ = 0
Решение этого уравнения будет иметь вид:
φ(x) = сe±qx
q2(ħ2/2m) φ(x) + (E - u0) φ(x) = 0
q = (2m(u0 - E)/ ħ2) ½
Тогда решением будет:
φ(x) = сe-qx + Deqx
Заметим, что решение вида eqx не подходит, так как не удовлетворяет условию нормировки. Поэтому решение будет φ(x) = сe-qx
Таким образом, в области x > 0 существует отличная от нуля волновая функция и существует вероятность обнаружить частицу за потенциальным барьером. Для того, чтобы найти коэффициент отражения, напишем условие непрерывности волновой функции и ее производных в точке x = 0.
А + B = C
dφ/dx= ikAeikx - ikBe-ikx
dφ/dx = - qce-qx
ikA – ikB = -qc = -q(A + B)
A = [(ik-q)/(ik+q)]B
k = |B/A|2 = |(ik-q)/(ik+q)| 2 = 1
Из этого следует, что в области x < 0 вероятности обнаружить частицу, движущуюся к барьеру, и отраженную частицу одинаковы. Так как решение было найдено при Е = const, то неопределенность времени ∆t → 0.
Рассмотрим движение частицы с потенциальным барьером вида
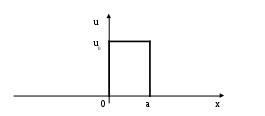
Предположим, что частица находилась сначала в области x < 0. Ее энергия Е < u0. Тогда решение стационарного уравнения Шредингера будет иметь вид в областях:
1) x < 0
φ(x) = Aeikx + Be-ikx
2) 0φ(x) = сe-qx ; q = (2m(u0 - E)/ ħ2)1/2
3) x > a
φ(x) = Deikx (отраженной частицы нет)
Таким образом, существует вероятность, что частица может пройти потенциальный барьер из области x < 0 в область x > a. Эта вероятность характеризуется коэффициентом пропускания, который равен квадрату модуля отношения волновых функций ψ(а) и ψ(0).
T = |ψ(а)/ψ(0)|2 = |φ(а)/φ(0)| 2 , так как ψ(x,t) = φ(x)e –iωt
T = |сe –qa/ce –q0|2 = e –2qa
Таким образом, если потенциальный барьер бесконечно широкий (а → ∞), то Т равно нулю. Если u0 → ∞ (высота потенциального барьера), Т также равно нулю.
|
|
|
 Скачать 0.99 Mb.
Скачать 0.99 Mb.