лекции по физике - 1 курс 2 семестр. Лекции по физике за второй семестр
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
|
Лекции по физике за второй семестр I курса Студентка группы СС0604 Пунякова Анастасия Часть III. Колебания и волны. Глава 1. Колебания. § 1.1. Свободные гармонические колебания. Уравнение и начальные условия. Число независимых переменных необходимых для описания механической системы называется числом степенней свободы. Рассмотрим систему с одной степенью свободы, при описании которых будем использовать одну переменную. Это может быть либо координата, либо заряд, либо угол, и т.п.. В целом ряде задач эта переменная удовлетворяет уравнению вида: В качестве примера такой системы рассмотрим пружинный маятник без трения: 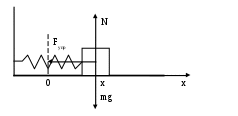 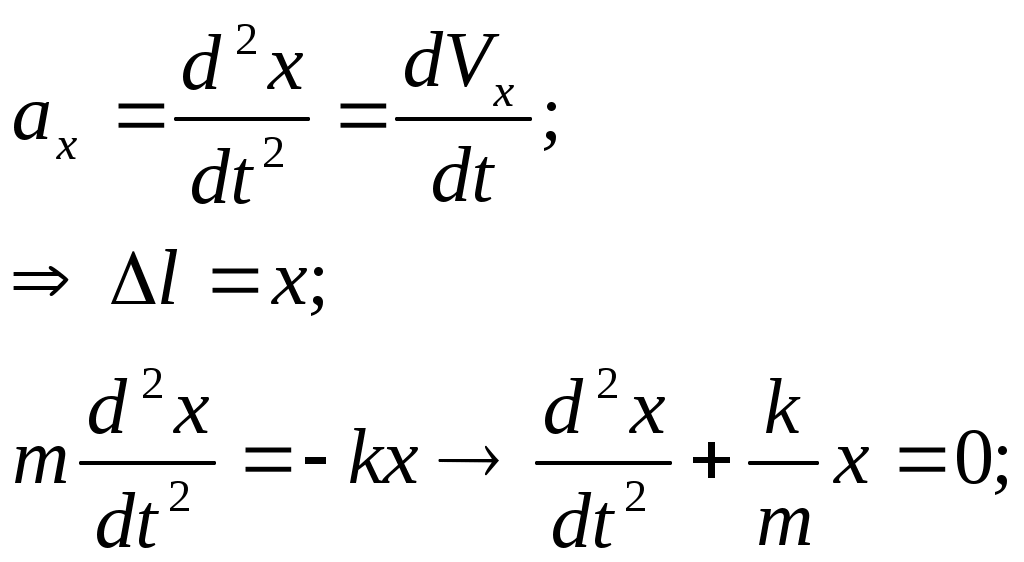 Заменим соотношением: Уравнение, изложенное выше называется линейным, дифференцируемым уравнением второго порядка. Будем искать переменную Последнее выражение есть уравнение гармонических колебаний. Система, которая описывает уравнение гармонических колебаний, называется гармоническим осциллятором. 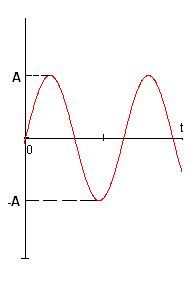 амплитуда колебаний; амплитуда колебаний;СИ: T – время, в течение которого фаза колебаний меняется на Также есть ещё одна величина, характеризующая колебания, – частота колебаний: Если Полученное решение содержит две производные постоянных величин A и 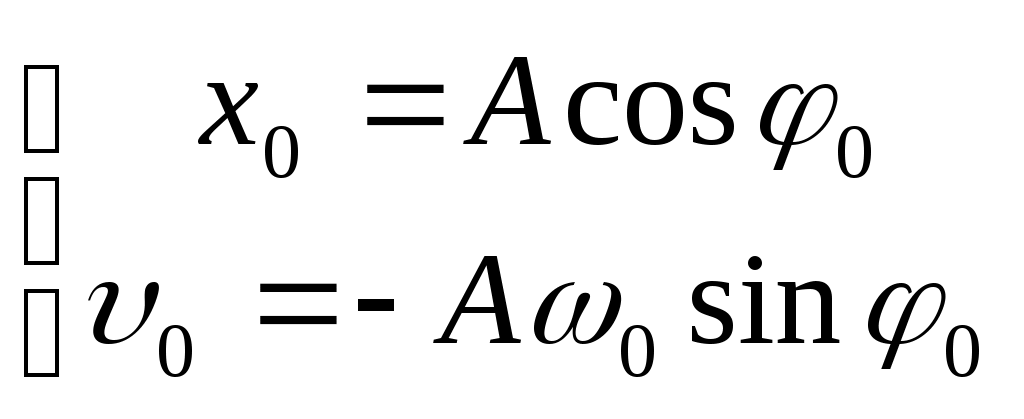 Отсюда получим Амплитуда будет равна 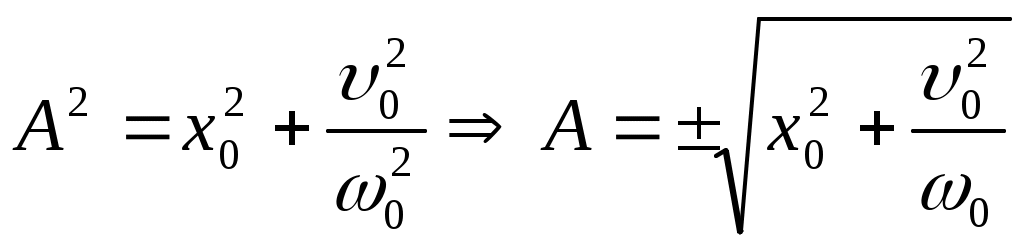 . .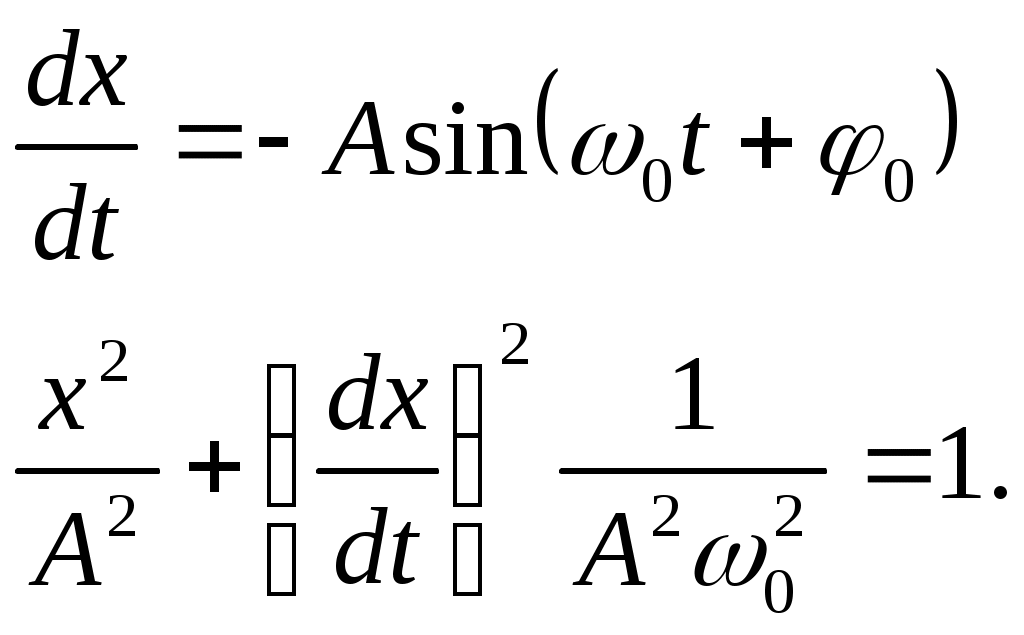 § 1.2. Затухающие колебания. Рассмотрим систему, в которую есть сила трения, пропорциональная скорости. 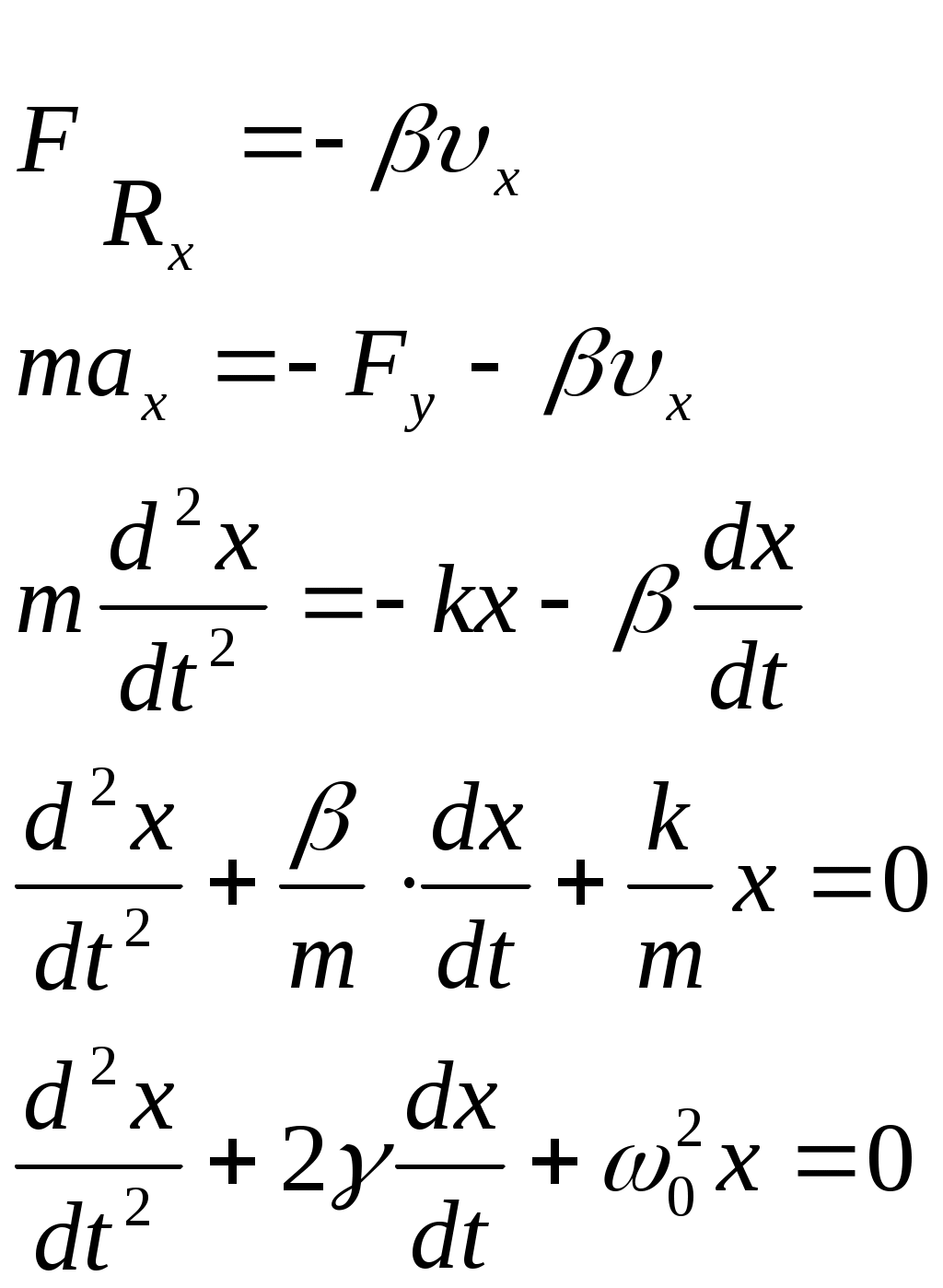 Надо учесть что Решение затухающих колебаний: Рассмотрим уравнение, в котором xкомплексная величина. Очевидно, что реальная часть комплексного уравнения является уравнением затухающих колебаний. Поэтому реальная часть решения комплексного уравнения будет решение уравнением затухающих колебаний. 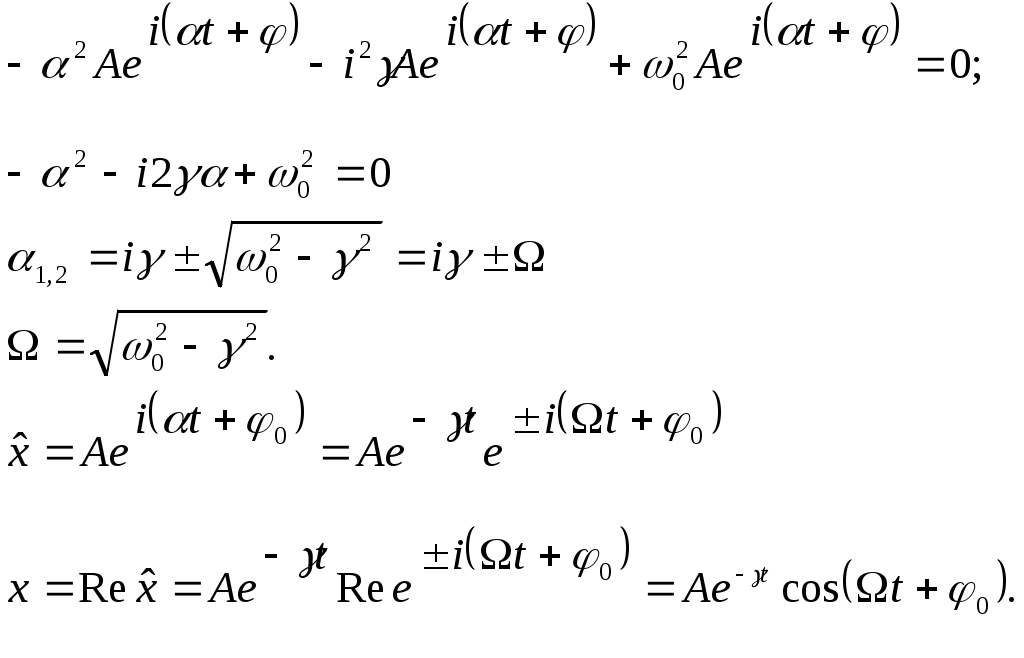 Периодом колебаний называется время, в течение которого фаза колебаний меняется на Время, в течение которого амплитуда колебаний уменьшиться в e раз, называется временем релаксации. 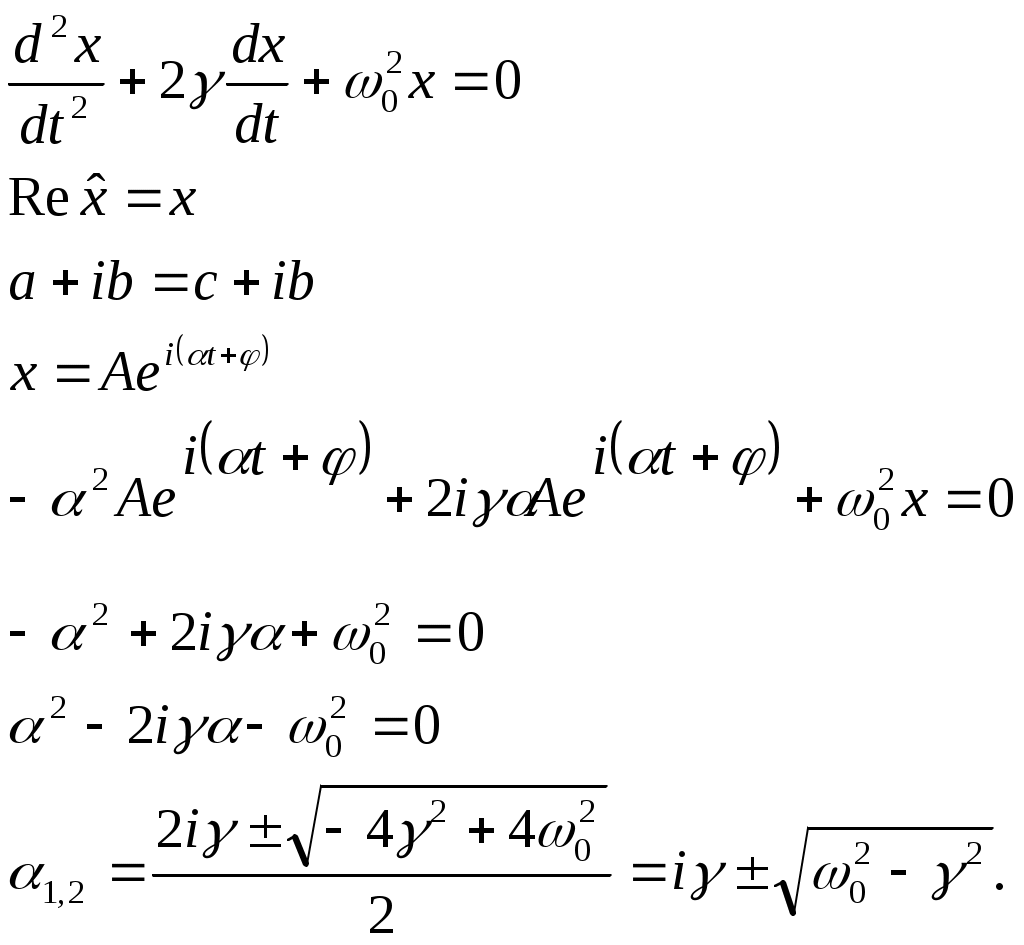 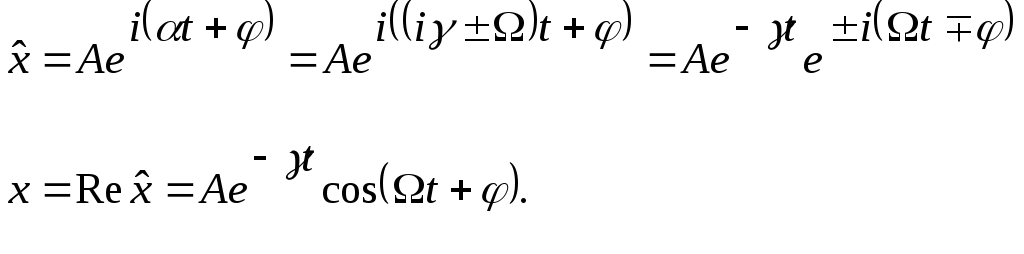 Логарифмическое отношение двух амплитуд разделенной одним периодом называется логарифмическим декрементом затухания. Заметим, что полученное решение будет справедливо, если Если 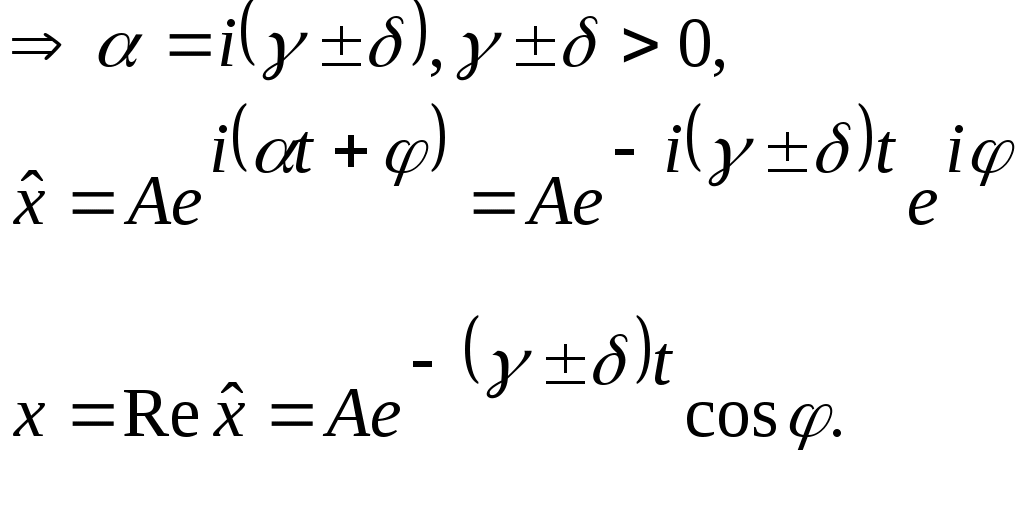 В этом случае никаких колебаний в системе не происходит, она просто стремится к положению равновесия, в зависимости от того, какие были начальные условия, в этом случае говорят, что в системе наблюдается «апериодический режим». Если § 1.3. Энергия свободных колебаний. Колебания рассмотренный в § 1.1 и § 1.2 принято называть свободными, так как они происходят в системах без воздействия внешних сил. Внешнее влияние происходит лишь в начальный момент времени, когда система выходит из состояния равновесия. Рассмотрим полную энергию гармонических колебаний на примере пружинного маятника, координаты которого Полная энергия 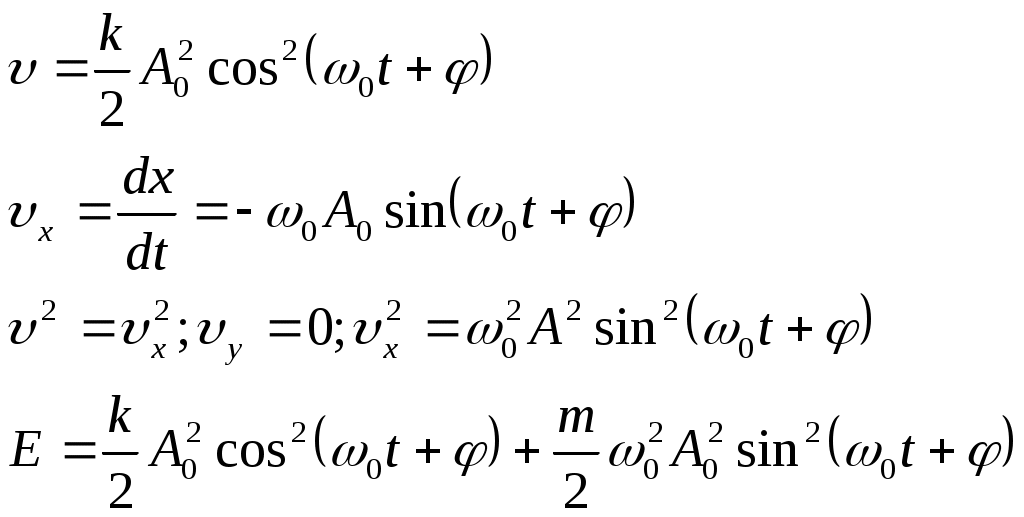 Учтём, что 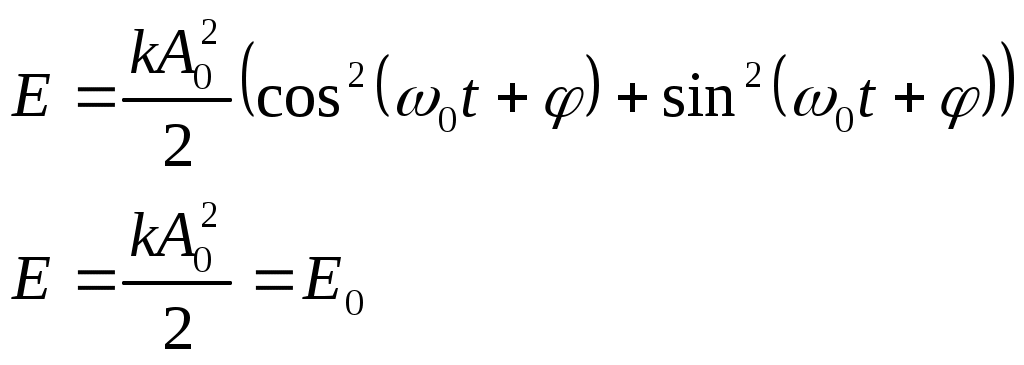 Полная энергия гармонических колебаний постоянна и пропорциональна квадрату амплитуду. Рассмотрим полную энергию затухающих колебаний пружинного маятника координата которого меняется по закону 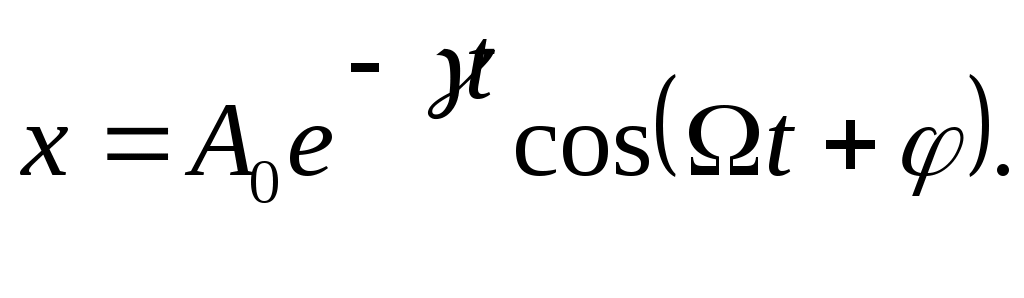 При этом будем считать, что затухание слабое, то есть При этом будем считать, что затухание слабое, то есть 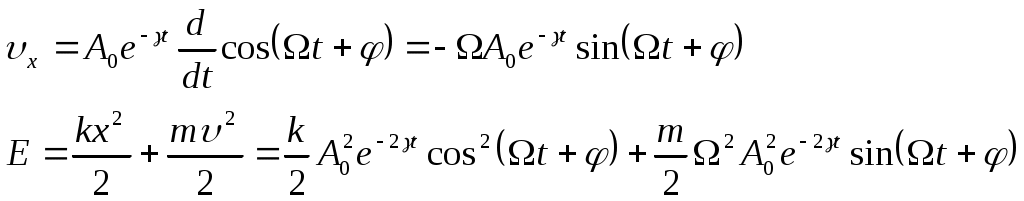 Знаем, что 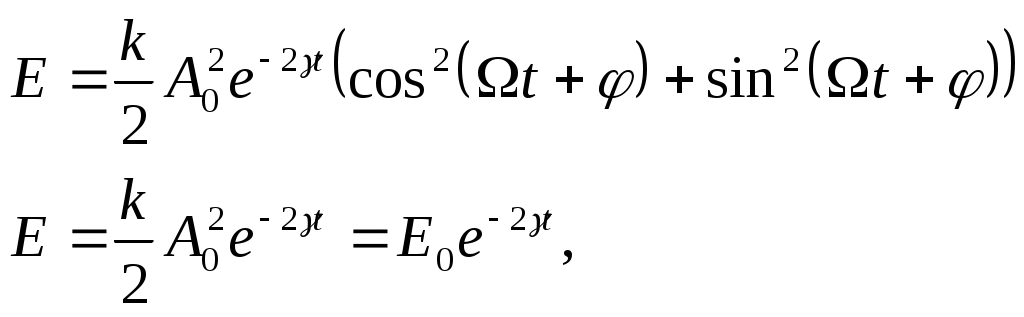 То есть энергия затухающих колебаний будет уменьшаться, точно так же как квадрат амплитуды. Добротность осциллятора называется: Q = 2П (энергия, запасенная осциллятором/ энергия, теряемая за период). Энергия, которую теряет осциллятор, будет: Зная добротность можно оценить, сколько колебаний со временем система выделит с помощью § 1.4. Вынужденные колебания. Анализ решения. Резонансные характеристики. Рассмотрим систему, на которую действует внешняя сила 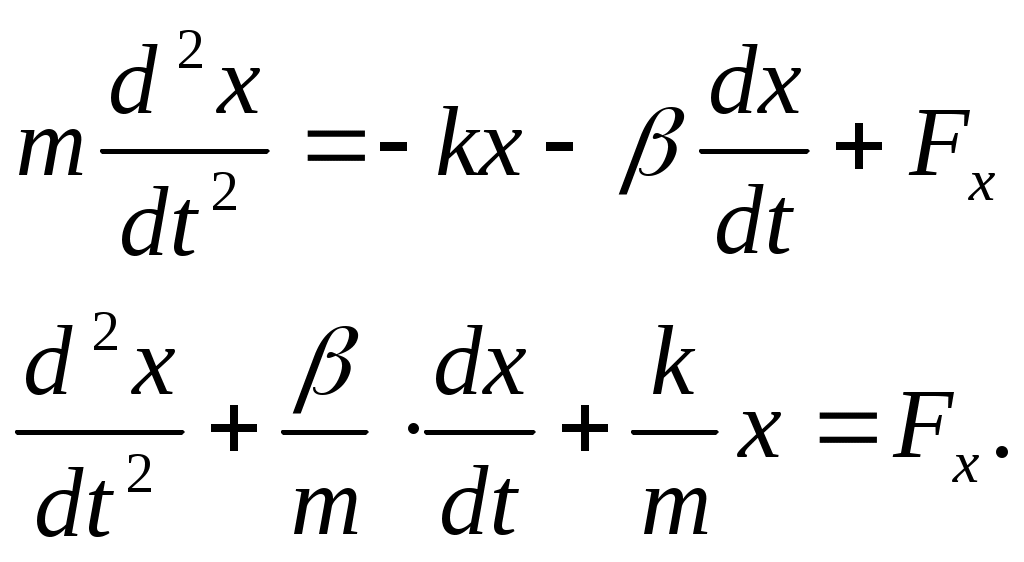 Рассмотрим самый важный случай, когда внешняя сила периодична. Тогда уравнение примет вид: Для того чтобы найти решение этого уравнения, рассмотрим комплексное уравнение реальная часть которого совпадает с нашим уравнением. 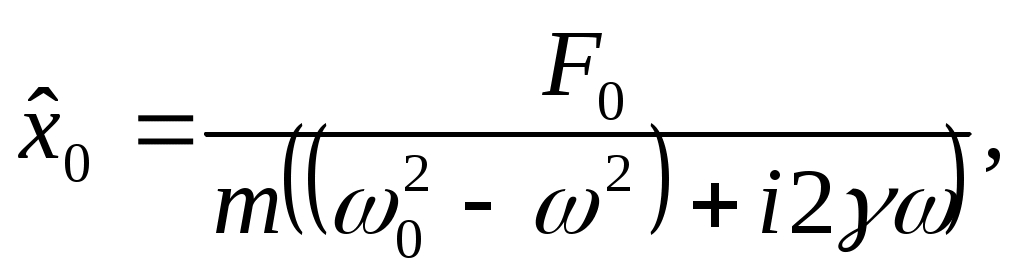 надо учесть, что надо учесть, что 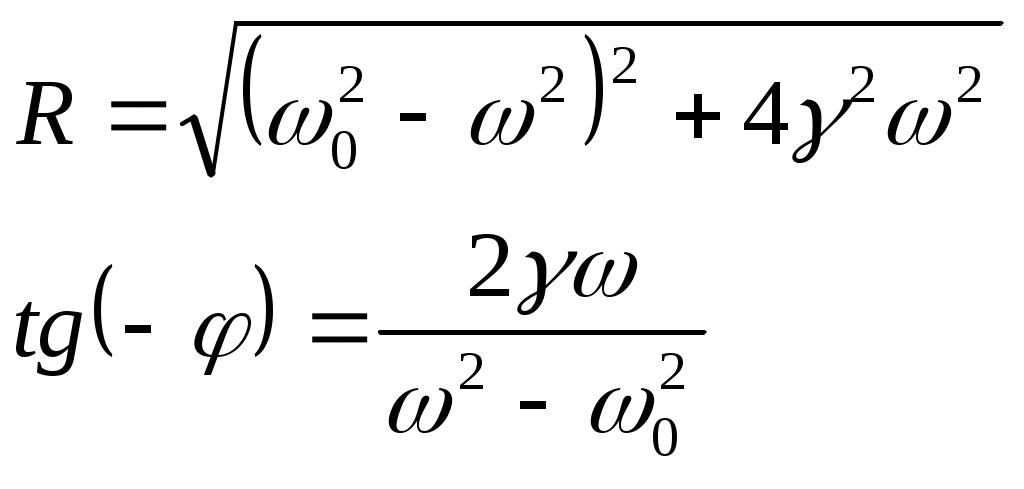 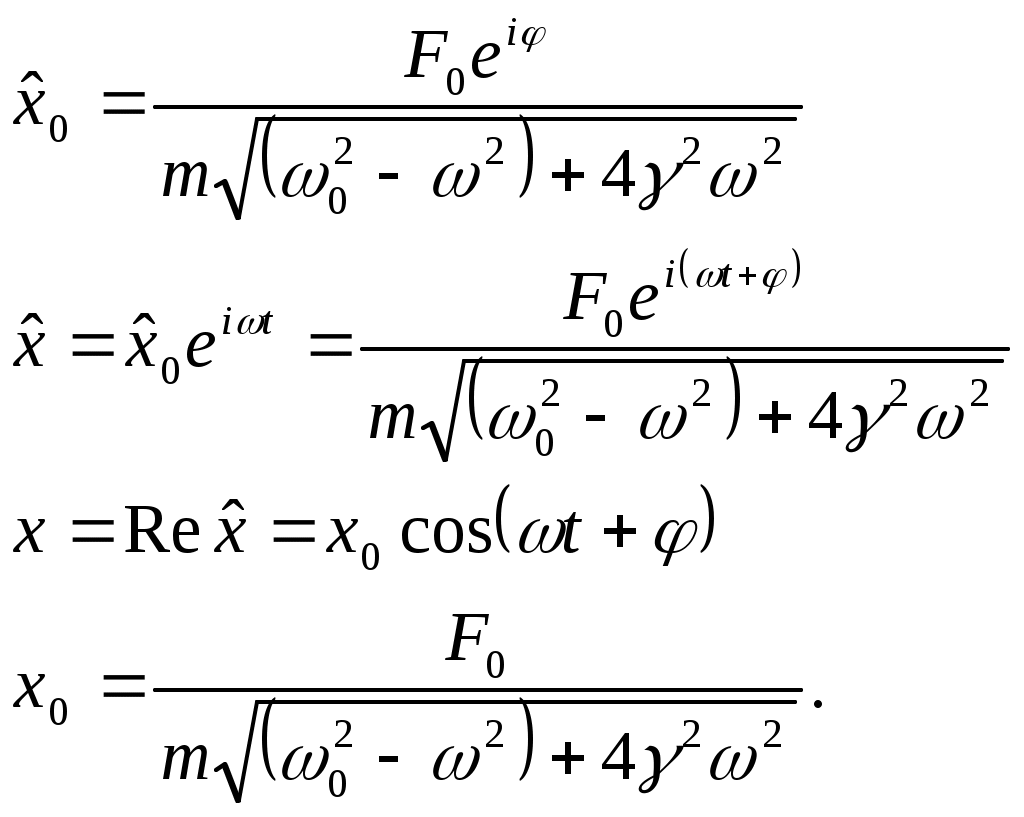 Таким образом, найденное решение уравнения вынужденных колебаний представляет собой гармонические колебания, амплитуда которых полностью определяется параметрами осциллятора и частотой ωR, при которой амплитуда максимальная, называется резонансной частотой. Если ω = ωR, говорят, что в системе наблюдается резонанс амплитуд. Для нахождения резонансной частоты надо приравнять к нулю Легко заметить, что достаточно прировнять к нулю производного подкоренного выражения Зависимость базового сдвига Рассмотрим скорость вынужденных колебаний: 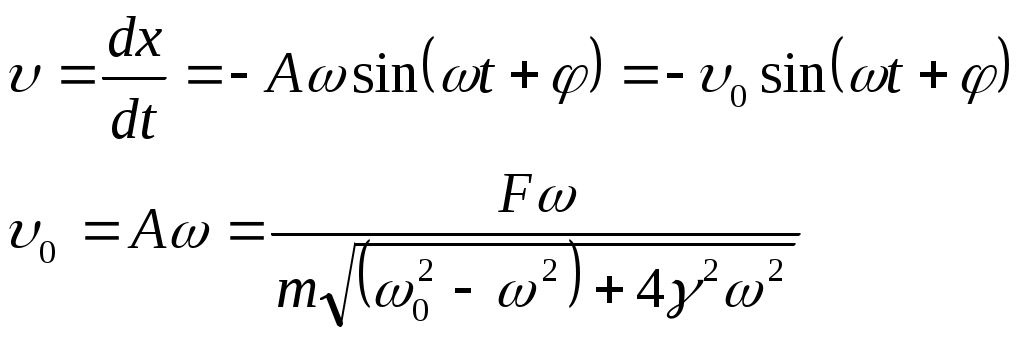 Последнее выражение называется амплитудой скорости. Полученная зависимость называется резонансом скоростей. Для определения частоты, при которой Полученное решение уравнения вынужденных колебаний представляет собой гармоническое колебание. В §1.3 говорилось, что полная энергия гармонических колебаний сохраняется, если сумма мощностей всех не потенциальных сил будет равна нулю. В нашей системе таких сил будет две: это сила трения и внешняя сила. Как известно мощность силы будет 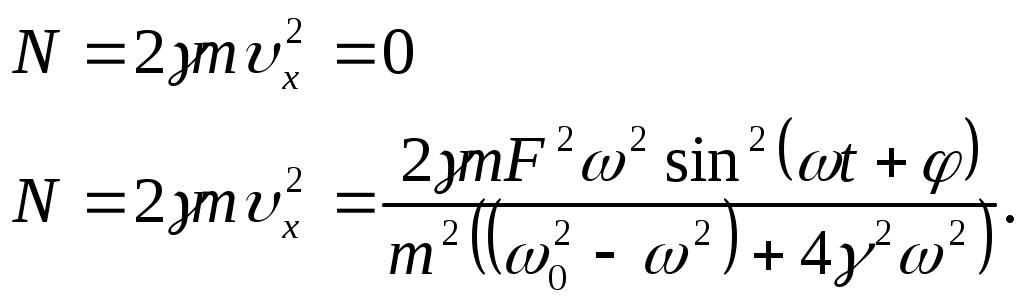 Очевидно, что среднее значение мощности вынужденной силы будет: 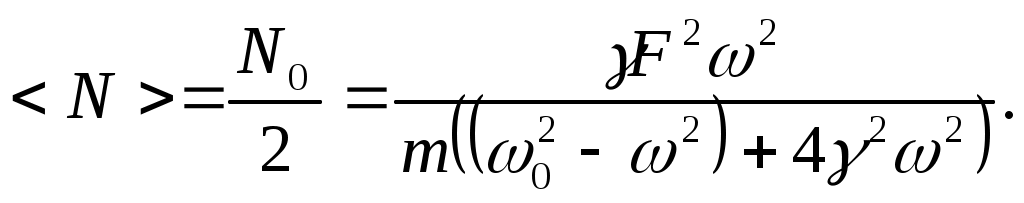 Так как средняя мощность частоты пропорциональна квадрату амплитуды скорости, то резонанс мощности будет происходить при той же частоте, что и резонанс скорости, то есть при собственной частоте. Осциллятор, в котором происходят вынужденные колебания, принято характеризовать полушириной ∆ω резонансной кривой, которая определяется на уровне половины максимальной мощности. Рассмотрим системы со слабым затуханием ∆ω << ω0, так как с уменьшением затухания ширина кривой уменьшается. Nm = γF2/4mγ2 Nm/2 = γF2/8mγ2 = F2/8mγ 8γ2ω0 = 4ω02∆ω2 + 4γ2ω02 ∆ω= γ |
