|
|
лекции по физике - 1 курс 2 семестр. Лекции по физике за второй семестр
§ 6. Частица в потенциальной яме. Дискретность энергетических состояний.
Рассмотрим частицу, которая находится в потенциальном поле, имеющем форму бесконечно глубокой ямы.
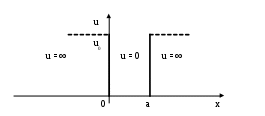
Как было показано в § 5, волновая функция частицы в области, где u > E , будет:
φ(x) e±qx , где q = q = (2m(u0 - E)/ ħ2)1/2
Если u → ∞, то q → ∞, а φ(x) → 0. Таким образом, в случае бесконечно глубокой ямы при x < 0 и x > a, φ(x) = 0, а если 0 < x < a, u = 0, тогда φ(x) = Aeikx+ Be-ikx (см. § 5)
k = (2mE/ ħ2)1/2
Из левого граничного условия следует:
φ(0) = 0 = B + A; B = -A
φ(x) = A(ekx – e-kx ) = C sin(kx)
Из правого граничного условия следует:
φ(a) = 0
sinka = 0; ka=Пn, где n = 1,2,3... (k = 0 - частицы нет)
k = (2mE/ ħ2)1/2
Е = ħ2 k2/2m = (ħ2/2m)(П2/a2) n2
Если частица находится в потенциальной яме, то ее энергетический спектр дискретен.
Е = Е0 = (ħ2/2m)(П2/a2) n2
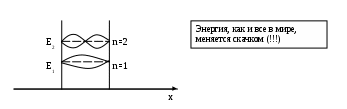

Таким образом, частица, которая находится в потенциальной яме, может принимать лишь дискретные значения энергии, и сила на такую частицу не действует. Условие дискретности энергетического спектра напрямую связано с характером движения частицы. Если движение частицы ограничено, то спектр дискретен, а если не ограничено, то ее энергетический спектр непрерывен. А если область ограничена, дискретный спектр неограничен и непрерывен.
§ 7. Атом водорода
Атом водорода состоит из тяжелого ядра и легкого электрона, поэтому центр масс находится почти в центре ядра.
Потенциальная энергия электрона в атоме водорода будет: u = qe2/4Пε0R
Если энергия электрона E < 0, то такой электрон находится в потенциальной яме, и его движение ограниченно атомом водорода.
Если Е становится > 0, то электрон выходит из потенциальной ямы и его движение становится неограниченным.
Рассмотрим сферически симметричный случай. Так как волновая функция ψ(R) сферически симметрична. В этом случае энергия электрона будет принимать дискретное значение.
En = - Er/n2 n = 1, 2, 3...
Er= 13,6 = const
n – главное квантовое число
В сферически симметричном случае волновая функция имеет вид
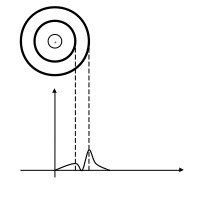
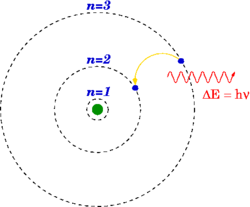
В сферически симметричном случае нельзя говорить о моменте импульса электрона равен нулю. Изменить энергию электрона можно лишь скачком (квантово). Чтобы увеличить энергию, электрон должен получить квант энергии от электромагнитного излучения (поглотить фотон). При уменьшении он излучает фотон.
∆E = ħω (энергия запуска фотона)
Если волновая функция электрона сферически несимметрична φ(R), то электрон может иметь момент импульса
L = [l(l+1)ħ] 1/2
Проекция момента импульса на производную ось Z будет mħ, где m - магнитное квантовое число, ħ – орбитальное квантовое число.
Lz = m ħ, где m = -l, … 0, 1, 2… l
Каждое квантовое число влияет на энергию состояния, и при этом спектры излучения/поглощения приобретают тонкую структуру. Наиболее вероятны такие переходы, при которых ∆l меняется на единицу.
§ 8. Принцип Паули. Периодическая таблица элементов.
В классической механике две одинаковые частицы (два электрона) всегда можно было различить, так как всегда можно было проследить за движением каждой из них. В квантовой механике не существует траектории движения частиц (принцип неопределенности), поэтому проследить за движением каждой частицы принципиально невозможно.
Рассмотрим две одинаковые частицы. Волновая функция первой частицы φ1, а второй φ2. Пусть первая частица находится в точке с координатами R1, а вторая соответственно R2. Тогда |φ1(R1)| 2 определяет плотность вероятности обнаружить частицу в точке с координатой R1. |φ2(R2)| 2 определяет возможность обнаружить частицу в точке с координатой R2.
Если частица независима, то совместная вероятность того, что первая частица находится в точке R1, а вторая при этом – в точке R2, должна быть равна произведению вероятностей. Общая функция двух частиц должна быть φ1(R1) φ2(R2) пропорциональная произведению двух волновых функций. Поменяем частицы местами. Тогда их общая волновая функция будет φ1(R2) φ2(R1).
То есть общая волновая функция частиц изменится, но так как частицы неразличимы, то от перемены мест частиц их общая волновая функция измениться не должна. Таким образом, полученные общие волновые функции частиц не удовлетворяют принципу неразличимости частиц. Для того чтобы выполнялись оба условия для общей волновой функции, необходимо, чтобы:
1) частицы были неразличимы
2) общая волновая функция зависела от произведения волновых функций
Тогда волновую функцию можно записать в виде:
φ12 = 0,5 [φ1(R1) φ2(R2) + φ1(R2) φ2(R1)]
Знак (+) надо ставить для волновых функций частиц с целым спином. Такие частицы называются частицами Бозе, или “бозонами”.
Знак (–) надо ставить для волновых функций частиц с полуцелым спектром. Такие частицы называются частицами Ферми, или “фермионами”.
Легко заметить, что в одной системе не может находится двух одинаковых фермичастиц с одинаковыми волновыми функциями.
φ12 = 0,5 [φ(R1) φ(R2) - φ(R2) φ(R1)] = 0
Так как состояние частицы определяется ее волновой функцией, а она в свою очередь определяется квантовыми числами частицы (n, l, m, S), то в одной системе не может быть двух частиц со всеми одинаковыми квантовыми числами.
Рассмотрим многоэлектронный атом.
Если в атоме находится один электрон, то он может иметь любые квантовые числа. При этом электрон всегда будет стремиться занять состояние с наименьшей энергией:
n = 1; l = 0; m = 0; S = ½
Если у атома два электрона:
n = 1; l = 0; m = 0; S = -½
Таким образом, в атоме гелия с n = 1 может находиться два электрона. Химические взаимодействия атомов – это результат электромагнитного взаимодействия. Так как каждый атом в целом нейтрален, что электрические взаимодействия между ними смогут существовать только за счет несимметричного расположения зарядов в атоме.
В атоме гелия все состояния с n = 1 полностью заполнены, поэтому электроны в атоме гелия располагаются симметрично относительно ядра и такой атом химически неактивен, что отличает гелий от водорода.
Электроны с одинаковыми главными квантовыми числами n образуют одну электронную оболочку. Если оболочка полностью заполнена, то распределение электронов относительно ядра симметрично и такой атом химически нейтрален. Оболочка с n =1 называется k-оболочкой.
Следующая оболочка L с n = 2. На этой оболочке может быть несколько электронов.
n =2; l = 0; m = 0; S = ±1/2
l = 1; m = 0; S = ±1/2
m = 1; S = ±1/2
m = -1; S = ±1/2
Для того чтобы полностью заполнить L-оболочку, необходимо 8 электронов. После того, как заполнена k-оболочка, третий электрон попадает на L-оболочку, для заполнения которой, как уже сообщалось, требуется 8 электронов. Поэтому литий очень химически активен. При постепенном заполнении L-оболочки химическая активность убывает, и, когда она полностью заполнена, мы получим инертный газ.
§ 9. Электрон в периодическом поле. Энергетические зоны.
Рассмотрим электрон, который находится в периодическом поле, представляющем собой последовательность потенциальных ям с интервалом d.
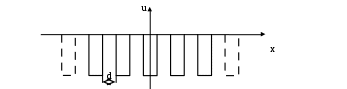
Предположим, что электрон находился в одной из этих ям, тогда за счет туннельного эффекта он может попасть с соседние ямы, не теряя энергию. То есть существует вероятность обнаружить электрон с той же самой энергией в любой яме. Так как все ямы одинаковы, то вероятность обнаружить электрон в любой из них одна и та же. То есть волновая функция электрона в таком поле будет одна и та же. Зависимость энергии электрона от волнового числа k в периодическом поле будет практически такой же, как у свободного электрона.
E = P2/2m = ħ2k2/2m
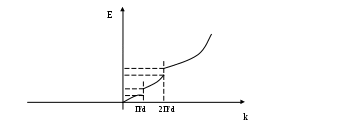
Однако в периодическом поле будут существовать некоторые особенности. Волновая функция электрона на каждой границе ям будет испытывать отражение. В общем случае все отраженные волны равны нулю, за исключением, когда отраженные волны находятся в фазе. Это возможно, когда геометрическая разность хода между отраженными волнами будет равна целому числу длин волн.
2d = nλ = 2Пn/k; λ = 2П/k
k = Пn/d - при таких k отраженные волны будут образовывать значительную отраженную волну, при сложении которой с падающей волной в системе возникает стоячая волна, то есть чередование узлов и пучностей.
При этом возможны два варианта:
1) пучность находится над ямой
2) узел находится над ямой
В первом случае говорят, что электрон захвачен ямой. Во втором случае говорят, что электрон находится вне ямы. Энергия электрона в этих случаях будет размыта.
Когда электрон находится в яме, его энергия будет меньше энергии свободного электрона. Когда электрон находится вне ямы, его энергия будет больше энергии свободного электрона.
Электрон в периодическом поле имеет непрерывный спектр энергии, так как его движение неограниченно, как и у свободной частицы. Влияние периодического поля приводит к возникновению в непрерывном спектре запрещенных зон энергии.
Рассмотрим кристаллическую решетку твердого тела. Потенциальная энергия электрона у каждого узла решетки представляет собой потенциальную яму. Если твердое тело имеет кристаллическое строение, то потенциальная энергия электрона внутри этого тела будет периодической последовательностью потенциальных ям. Движение электрона в твердом теле, таким образом, будет похоже на движение электрона в периодическом поле. Отличие состоит в том, что движение электрона в твердом теле ограничено размерами тела, что означает, что энергетический спектр в разрешенных зонах энергии будет дискретным. Из-за того, что размеры твердого тела много больше размера электрона, что интервал между ближайшими уровнями энергии будет ничтожно мал, и поэтому энергия электрона под действием внешнего поля может меняться непрерывно, то есть внешнее поле действует на электрон и его скорость при этом меняется. Электрон может двигаться под действием электрического поля.
Если электронов много, то картина резко изменяется. По принципу Паули в одном состоянии может находиться только один электрон. Если все состояния в разрешенной зоне энергии заполнены, то энергия электронов под действием внешнего поля измениться не может.
Валентная зона – последняя полностью заполненная зона энергии.
Зона проводимости – следующая зона за валентной.
Если между валентной и пустой зоной проводимости находится широкая запрещенная зона шириной ∆ε >> kT, то такое тело называется диэлектриком.
Если ширина запрещенной зоны ∆ε << kT или валентная зона полностью перекрывается зоной проводимости, то такое тело называется проводником.
Когда ∆ε ≈ kT, то такие тела называются полупроводниками.
Скорость электрона в твердом теле совпадает с групповой скоростью волны:
E = ħω
V = Vg = dω/dk = (1/ħ) (dE/dk)
a = dV/dt = (1/ħ)(d/dt)(dE/dk) = (d2E/dk2)(1/ħ)(dħk/dt) = (1/ħ2) (d2E/dk2)F
m = ħ2/(d2E/dk2) (1)
Такое представление поведения электрона в твердом теле называется зонной теорией. Суть зонной теории состоит в следующем: сложное взаимодействие электронов с внешним полем и ионами кристаллической решетки, заменяется некоторым ящиком формы твердого тела, в котором нет никаких ионов, а есть только электроны. Эти электроны ведут себя как свободные электроны с тем лишь отличием, что в их энергетическом спектре появляются запрещенные энергетические зоны и вместо массы электрона надо использовать эффективную массу (1)
ОГЛАВЛЕНИЕ:
Часть III. Колебания и волны
Глава 1. Колебания
§ 1.1. Свободные гармонические колебания. Уравнение и начальные условия………………...2
§ 1.2. Затухающие колебания……………………………………………………………………….4
§ 1.3. Энергия свободных колебаний……………………………………………………………....6
§ 1.4. Вынужденные колебания. Анализ решения. Резонансные характеристики………………7
§ 1.5. Вынужденные колебания. Переходный процесс……………………………………………9
§ 1.6. Сложение гармонических колебаний двух частот………………………………………….11
§ 1.7. Физические основы анализа Фурье………………………………………………………….13
Глава 2. Волны
§2.1. Волновой процесс. Волновая функция……………………………………………………….14
§ 2.2 Параметрические волны……………………………………………………………………….16
§2.3. Распространение волн в ограниченной среде. Стоячие волны……………………………...18
§2.4. Интерференция волн двух источников………………………………………………………..19
§2.5. Многолучевая интерференция…………………………………………………………………22
§2.6. Дифракция. Признак Гюйгенса………………………………………………………………..23
§2.7. Дифракционная решетка……………………………………………………………………….25
§2.8. Принцип Гюйгенса – Френеля. Дифракция Френеля………………………………………...26
§2.9. Волновой пакет…………………………………………………………………………………28
§2.10. Групповая скорость. Метода стационарных фаз……………………………………………30
§2.11. Пространственная и временная когерентность. Поляризация……………………………..31
§2.12. Приближение геометрической оптики. Уравнение Эйконала. Принцип Ферма………….33
§2.13. Электромагнитные волны в вакууме………………………………………………………...34
§2.14. Энергия электромагнитного поля. Вектор Умова-Пойнтинга……………………………..35
Часть IV. Квантовая механика
§ 1. Экспериментальные основы квантовой механики…………………………………………….37
§ 2. Волны де Бройля…………………………………………………………………………………38
§ 3. Уравнение Шредингера………………………………………………………………………….39
§ 4. Принцип неопределенности Гейзенберга………………………………………………………41
§ 5. Движение частицы в поле с потенциальным барьером. Туннельный эффект……………….42
§ 6. Частица в потенциальной яме. Дискретность энергетических состояний…………………...44
§ 7. Атом водорода……………………………………………………………………………………46
§ 8. Принцип Паули. Периодическая таблица элементов………………………………………….47
§ 9. Электрон в периодическом поле. Энергетические зоны……………………………………...49
|
|
|
 Скачать 0.99 Mb.
Скачать 0.99 Mb.