теория информации. ТИ (Best). Лекции по предмету "Теория информации" Красноярск 2002
 Скачать 1.06 Mb.
|
Количественное определения избыточностиНаличие вероятностных зависимостей между элементами сообщения уменьшает количество информации, приходящейся на каждый элемент сообщения. Пример, который подтверждает справедливость данного утверждения. Пример: Пусть имеется два элемента a, в. Рассмотрим случаи передачи информации с помощью этих элементов: 1) Элементы независимы и равновероятны  1 бит/символ m – количество переданных символовЭлементы независимы и неравновероятны    бит/символЭлементы взаимозависимы и равновероятны p(a) = p(b) = ½ Пусть p(a / a) = p(b / b) = p1 – вероятность повторения символов p(a / b) = p(b / a) = p2 - вероятность чередования символов 
Элементы взаимозависимы и неравновероятны p(a) = ¾; p(b) = ¼ p(a / a) = 2/3 p(b / a) = 1/3 p(a / b) = 1 p(b / b) = 0 I| =  =  0.685 бит/символПусть передаётся сообщение из n взаимозависимых и не равновероятных элементов. I = n * I| Если устранить внутренние вероятностные связи, то информация возрастёт до максимального значения Imax . При этом тоже количество информации может содержаться в сообщении из меньшего числа элементов n0.  В данном случае мерой избыточности может служить относительное число лишних элементов. Обозначим избыточность символом D. - мера избыточностиЕсли принять, что избыточность определяется только взаимосвязью элементов, то  Если принять, что избыточность определяется только распределением вероятностей, то в качестве  , m – количество элементовТаким образом, выделяют две частных избыточности: Частная избыточность, обусловленная взаимосвязью между элементами 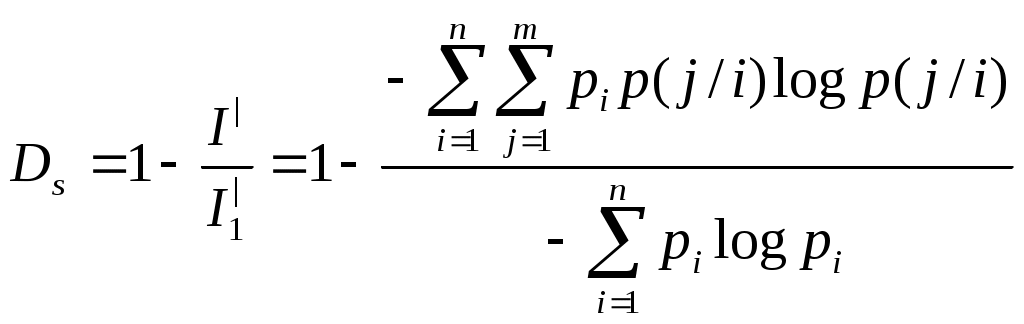 Частная избыточность, зависящая от распределения вероятностей 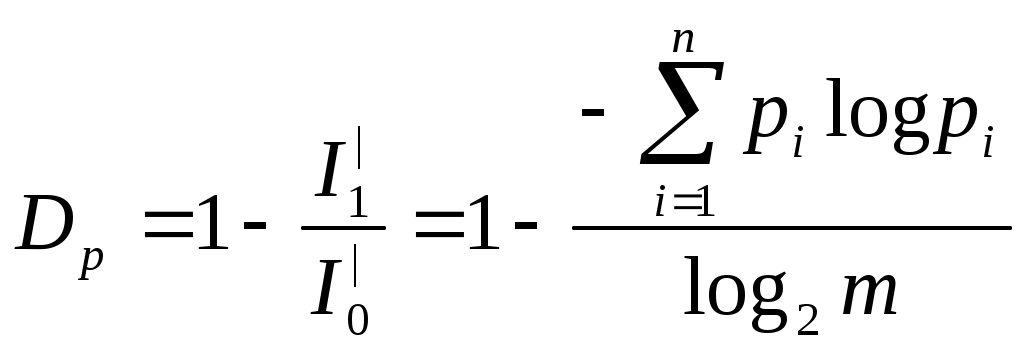 m – количество символов алфавитаВыделяют полную информацию избыточность D = Dp + Ds – DpDs  Dp + ВыРассмотрим основные цифры и порядки для рассмотрения примера  - относительная величина Ds * Dp = 0.03 принебрегаем Пример избыточности в нашем языке можно проиллюстрировать следующими цифрами. Если бы все комбинации букв были возможны, то имея 30 букв, можно было бы составить 301 = 30 однобуквенных слов. 302 = 900 – двухбуквенных слова. 303 = 27 000 – трёхбуквенных слова. 304 = 810 000 – четырёх буквенных слова. Обычный язык содержит 50 000 слов, т.е. среднее число букв в слове, составляет примерно 3,5. В обычном в языке среднее число букв в слове семь, следовательно, возможные комбинации 307 = 21 * 109 - столько слов можно было бы иметь, следовательно, количество букв, которые являются словами =  . Один из методов борьбы с избыточностью применение неравномерных кодов. Метод построения оптимального неравномерного кода Шеннона - Фана. Пусть в алфавите имеется n букв и вероятности появления этих букв. Расположим эти буквы в порядке убывания их вероятностей. Затем разбиваем их на две группы так, чтобы суммарная вероятность в каждой группе по возможности была одинаковой (верхнюю группу кодируем единицей, а нижнюю нулём). Это будет первый символ кода. каждую из полученных групп делим снова на две части возможно близкой к суммарной вероятности, присваиваем каждой группе двойной символ: (один или ноль). Процесс деления продолжаем, пока не придём к первой группе. Пример: Данный алфавит, содержит шесть букв.
  В случае равномерного кодирования потребовалось бы три бита (23 = 8). Для данного кода  Длина буквы 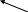 бит/символ Подсчитаем энтропию данного алфавита  бит/сим m – количество символов вторичного алфавитаЕсли вторичный алфавит – двоичный, то m = 2, следовательно  .Пример: Задан алфавит из восьми букв и вероятности их появления. Построить оптимальный неравномерный код Шеннона-Фана.
 бит бит/символКоэффициент статического сжатия 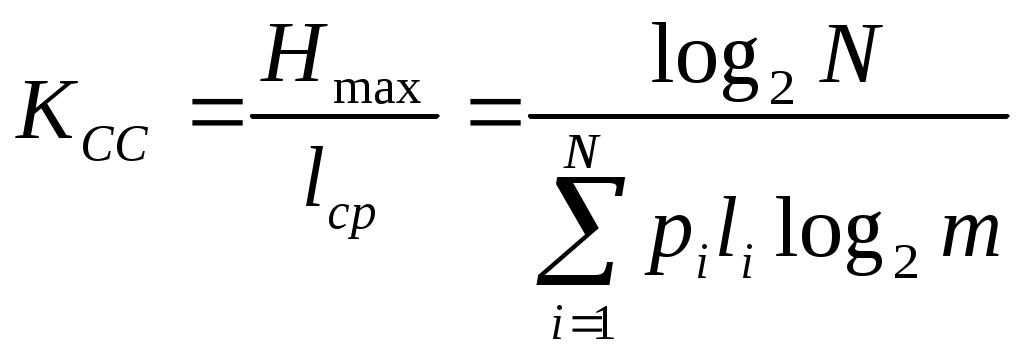 Коэффициент общей эффективности 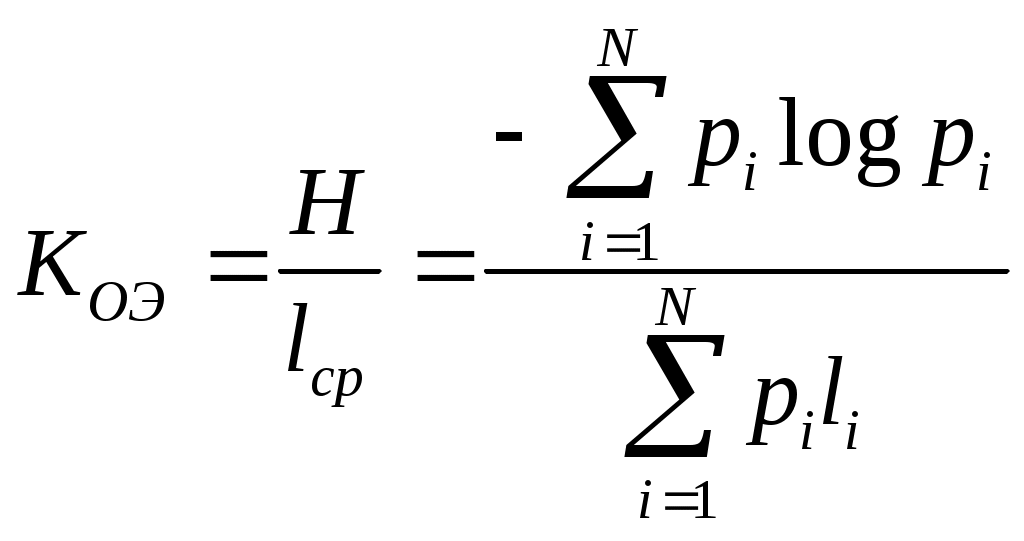 КСС и КОЭ характеризуют оптимальность алфавита Пример: Построить оптимальный код Шеннона-Фана. 
lср = 2.4 бит  бит/символ – т.к. разделили неравномерно три столбца, лучше не получиться.  |
