теория информации. ТИ (Best). Лекции по предмету "Теория информации" Красноярск 2002

• Название: Лекции по предмету "Теория информации" Красноярск 2002
• Анкор: теория информации
• Дата: 10.12.2022
• Размер: 1.06 Mb.
• Имя файла: ТИ (Best).doc
• Тип: Лекции; #837351
• страница: 3 из 12

Энтропия сложной системы

Под объединением двух систем X и Y с возможными состояниями x₁,x₂,…,x_n , y_1, y_2,…,y_{m ,} понимается сложная система (x, y), состояние которых x_i,y_i; представляют собой все возможные комбинации состояний x_i,y_i .

Число возможных состояний равно m х n.

Обозначим символом p_i,j , вероятность того, что система может находиться в состоянии p(x_i,y_i). Тогда вероятность p_ij можно представить в виде таблицы совместных вероятностей.

таблица совместных вероятностей xi & yi	x1	x2	…	xn
y1	p11	p21	…	pn1
y2	p12	p22		pn2
…	…	…	…	…
ym	p1m	p2m	…	pnm

; ; H(x, y) = M[- log p(x, y)].

Пусть системы X, Y независимы. Тогда по теореме умножения вероятностей имеем:
p(x, y) = p(x) * p(y)
Прологарифмируем левую и правую часть
log p(x, y) = log p(x) + log p(y)
H(x, y) = M[- log p(x) – log p(y)]
H(x, y) = H(x) + H(y), если независимые системы, то их энтропии складываются.

Условная энтропия. Объединение зависимых систем.

Пусть имеем две зависимые системы X и Y. Пусть система X приняла состояние x_i, а система Y приняла состояние y_i , тогда обозначим p(y_{i /} x_i) – это условная вероятность того, что система Y примет состояние y_i, при условии, что система X приняла состояние x_i.

Неопределённость системы в состоянии Y определяется частной условной энтропией.

- система X находится в конкретном состоянии

; - условное математическое ожидание

Полная условная энтропия

Для определения полной условной энтропии, каждая частная условная энтропия умножается на вероятность соответствующего состояния и все произведения складываются.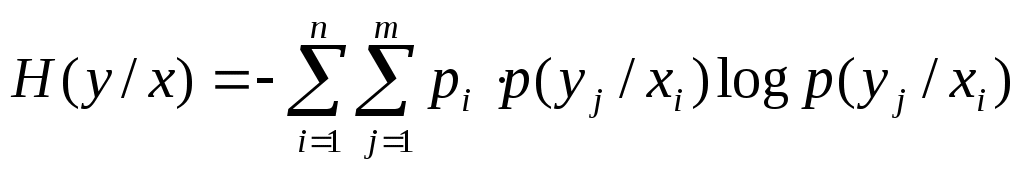

p_i = p(x_i) – вероятность наступления события x_i

;
p_i * p(y_j / x_i) = p_ij
Тогда
; H(Y / x) = M[ - log P(y / x)]

В целом полная условная энтропия характеризует степень неопределённости состояния системы Y, оставшуюся после того, как состояние системы X полностью определилось.
Пример: Имеются две системы, объединённые в одну, вероятности состояния которых заданы таблицей совместных вероятностей. Определить полную условную энтропию.

Определим вероятности каждого события. Для этого складываем p_ij по столбцам.

xi & yi	x1	x2	x3	rj
y1	0.1	0.2	0	0.3
y2	0	0.3	0	0.3
y3	0	0.2	0.2	0.4
pi	0.1	0.7	0.2

Построить таблицу условных вероятностей p(y / x). в каждой строке

yi& xj	x1	x2	x3
y1	1	0.2/0.7	0
y2	0	0.3/0.7	0
y3	0	0.2/0.7	1

бит/символ
Составим таблицу условных вероятностей P(x / y).

xi& yi	x1	x2	x3
y1	0.1/0.3	0.2/0.3	0
y2	0	1	0
y3	0	0.2/0.4	0.2/0.4

H(x / y) = 0.3[(0.1/0.3) + (0.2/0.3)]+ 0.4[(0.2/0.4 + (0.2/0.4)] = 0.68 бит/символ
Н - характеризует потери сигналов при прохождении через канал связи.

Теорема сложения энтропий
Если две системы X и Y объединятся в одну, то энтропия объединений системы равна энтропии одной из систем плюс условная энтропия второй системы относительно первой.
H(x, y) = H(x) + H(y / x)
Доказательство этой теоремы:
Запишем H(x, y) через. математическое ожидание
H(x, y) = M[ - log p(x, y)]
По теореме умножения вероятностей
p(x, y) = p(x) * p(y / x)
log p(x, y) = log p(x) + log p(y / x)
M[x, y] = M[ - log p(x)] + M[ - log p(y / x)]
H(x, y) = H(x) + H(y / x)
Интерес представляют частные случаи:

• 
  Когда системы независимы, условная энтропия H(y / x) = H(y) и получаем теорему сложения энтропий H(x, y) = H(x) + H(y).
  

H(x, y)  H(x) + H(y)

• 
  Когда состояние одной системы X полностью определяет состояние другой системы Y. В этом случае условная энтропия равна нулю.
  

H(y / x) = 0 H(y, x) = H(x)
Пример: Передаются два элемента a, b. Определить количество переданной информации в случае, когда:

1) Элементы взаимозависимы и не равновероятны
p(a) = ; p(b) = ; p(a / a) = p(b / a) =

p(b / b) = 0 p(a / b) = 1
I = H – вероятность события а

I = H = - p(a)[ p(a / a) log p(a / a) + p(b / a) log p(b / a) ] – p(b)[ p(a / b) log p(a / b) + p(b / b) log p(b / b)] = 0.685 бит/символ .
2) не равновероятны и независимы:
p(a) = _; p(b) =

I = - p(a) log p(a) – p(b) log p(b) = - log - log = 0.815 бит/символ
3) элементы независимы и равновероятны:
p(a) = p(b) = ; I = log₂ = 1