теория информации. ТИ (Best). Лекции по предмету "Теория информации" Красноярск 2002

• Название: Лекции по предмету "Теория информации" Красноярск 2002
• Анкор: теория информации
• Дата: 10.12.2022
• Размер: 1.06 Mb.
• Имя файла: ТИ (Best).doc
• Тип: Лекции; #837351
• страница: 1 из 12

Кафедра ИУС

Лекции по предмету

"Теория информации"

Красноярск 2002

Информация. Язык. Общество

Всякий организм, в том числе и общ-й скрепляется наличием средств использования, хранения и передачи информации. Очень мало стабилизирующих процессов.

Теория информации развивалась как наука в конце 40-х г.г. В её основу положены труды Шеннона, Винера, Колмогорова, Котельникова. Это полуматематическая наука, т.е. прикладное приложение к математике.

Измерение информации

Важным вопросом в теории информации является установленные меры информации. В качестве меры информации выделяют структурные и статические меры. Структурные меры рассматривают дискретное строение массивов информации и измеряют информацию подсчётом числа возможных информационных измерений. Статические методы учитывают вероятность появления информационных символов и в качестве меры информации используют понятие энтропия – мера неопределённости состояния систем.

Структурный метод

Структурные методы имеют дело с информационными массивами. Массив информации представим в виде кубика.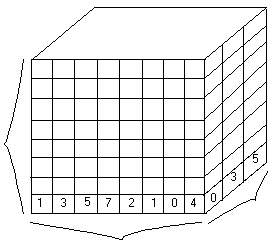




n – длина передаваемого числа;

m – глубина числа;

Поле – набор из элементов чисел m из гнезда выдвигаются нужное число,

а число определено.

поле

m

- гнездо


n


Все ячейки называются числовой грядой (один слой). Совокупность слоев – это поле.

Количество чисел, которое может быть представлено с помощью одной числовой гряды:

В 1928г американец Хартли предложил использовать логическую меру: - это мера информации по Хартли (аддитивная мера по Хартли) количество информации, измеренное такой мерой, измеряется в битах (это название даёт основание log₂). Если глубина числа m = 2 – это двоичная мера информации (0 или 1), если m = 1, то кол-во информации равно один бит. Это соответствует одному элементарному событию.

Статический метод

Обычно элементы сообщений не равновероятны, и это обстоятельство влияет на количество переданной информации. Пусть имеется алфавит из m элементов h₁, h₂, …,h_m – элементы алфавита. Вероятности появления символов равны p₁, p₂, …,p_m. Составим из этих элементов сообщения, содержащее n элементов. Среди них будут n₁ элементов h₁, n₂ элементов h₂, … n_m элементов h_m .

Предположим, что появление каждого элемента независимое событие. Тогда вероятность появления определённой комбинации выражается произведением единичных вероятностей отдельных элементов и эту вероятность можно записать:



При достаточно большой длине числа n, можно считать, что n_i определяется как p_i*n. Кроме того можно считать, что все сообщения равновероятны, тогда вероятность отдельного сообщения: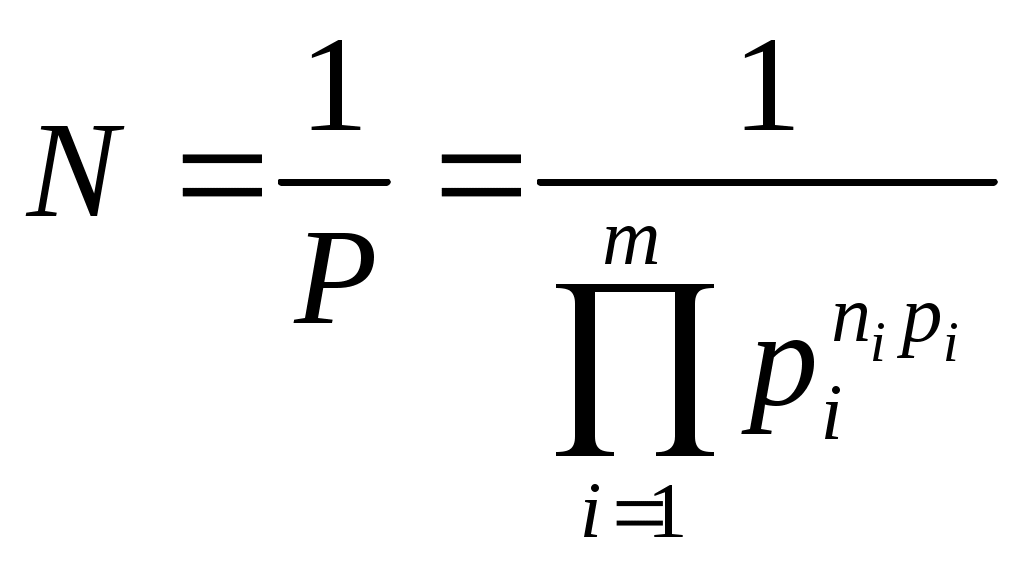
N – количество переданных сообщений;

I = log₂N – количество информации =
Кол-во информации, отнесённое к одному символу

- энтропия

Такая мера информации была введена Шенноном. Количество информации по Шеннону определяется как I. Измеряется [бит/символ]. Она характеризует количество переданной информации при неравновероятности появления символов и характеризует неопределённость состояния сообщения.