теория информации. ТИ (Best). Лекции по предмету "Теория информации" Красноярск 2002

• Название: Лекции по предмету "Теория информации" Красноярск 2002
• Анкор: теория информации
• Дата: 10.12.2022
• Размер: 1.06 Mb.
• Имя файла: ТИ (Best).doc
• Тип: Лекции; #837351
• страница: 5 из 12

Энтропия и информация

Пусть имеется система X с энтропией H(x). После получении информации о состоянии системы; система полностью определилась, т.е энтропия равна нулю, следовательно, информация, получаемая в результате выяснения состояния системы x равна уменьшению энтропии.
I_x = H(x) – 0 = H(x)
Количество информации приобретённое при полном выяснении состояния системы равна энтропии.
- часть информации о системе
- называют частной информацией о системе или информацией от отдельного сообщения.

Для системы с равновозможными состояниями



Полная информация


Пример: На шахматной доске в одной из клеток поставлена фигура. Вероятность нахождения фигуры на любой клетке одинакова. Определить информацию, получаемую от сообщения о нахождении фигуры в какой-либо клетке.
I_x = log 64 = 6 бит
Пример 2: Определить частную информацию от сообщения о нахождении фигуры в одной из четырёх клеток.
P = ; - вероятность сообщения = 4 бит
Пример 3: Определить частную информацию, содержащаяся в сообщении случайного лица о своём дне рожденье.
- вероятность полученного сообщения; бит – количество информации

Пример 4: Определить полную информацию от сообщения о дне рождения случайного лица.
x₁ – день рожденье

x_{2 –} не день рожденье
бит
Пример 5: По цели может быть произведено n выстрелов. Вероятность поражения цели при каждом выстреле p. После k-ого выстрела (1 к  n) производятся разведка, сообщение поражена или не поражена цель. Определить к при условии, чтобы количество информации, доставляемая разведкой была максимальной.

x_k – система (цель после к-ого выстрела) имеет два состояния:

x_{1 –} цель поражена;

x₂ – промах
p₁ = 1 – (1 - p)^k p₂ = (1 - p)^k
Информация будет максимальна, когда p₁ = p_2, следовательно

1 – (1 - p)^k = (1 - p)^k , k =

p = 0.2; к = 3

Взаимная информация

Имеется две системы: X и Y. Они взаимосвязаны. Необходимо определить, какое количество информации по системе X даст наблюдение за системой Y. Такую информацию определяют, как уменьшение энтропии системы X в результате получения сведений о системе Y.
I_yx = H(x) – H(x / y)

I_yx = I_xy = I_xy

1. 
   Если системы X и Y независимы, то
   

H(x / y) = H(x) и I_yx = 0 - информации не будет

2) Система полностью зависимы

H(x / y) = H(y / x) = 0 I_yx = H(x) = H(y)
Выражения для взаимной информации можно получить через взаимную энтропию

H(x / y) = H(x, y) – H(y) I_yx = H(x) + H(y) – H(x, y)
Формула для расчёта взаимной информации

H(x) = M[ - log p(x)], H(y) = M[ - log p(y)] H(x, y) = M[ - log p(x, y)]
I_yx = M[ - log p(x) – log p(y) + log p(x, y)]
П

Сумма равна единице

Этих сведений достаточно, чтобы определить взаим-

ную информацию, создавшуюся в системе


ример: Найти полную взаимную информацию, содержащуюся в системах X и Y. Если задача на матрицы совместных вероятностей.

xi & yi	x1	x2	x3	rj
y1	0.1	0.2	0	0.3
y2	0	0.3	0	0.3
y3	0	0.2	0.2	0.4
pi	0.1	0.7	0.2

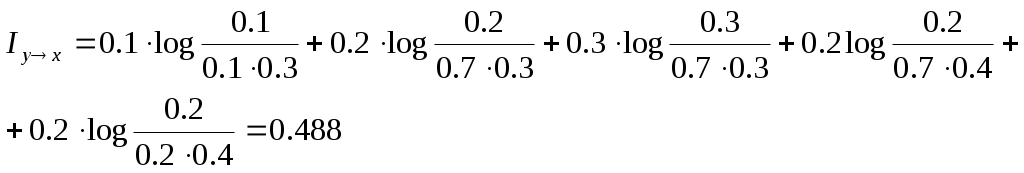бит