теория информации. ТИ (Best). Лекции по предмету "Теория информации" Красноярск 2002
 Скачать 1.06 Mb.
|
Блочное кодированиеПусть первичный алфавит содержит 2-е буквы: а и б. p(A) = 0.7; p(B) = 0.3 H = - 0.7*log 0.7 – 0.3 log 0.3 = 0.881 бит/символ Составим новый алфавит из 2-х буквенных комбинаций
Lср = 1 * 0.49 + 2 * 0.21 + 3 * 0.21 + 4 * 0.09 = 1.81 бит На одну букву  бит < 1 lср > H 3%Пример: Составим алфавит из трёх буквенных комбинаций.
lср = 2.686 бит  .895 бит - это больше 1,5% и H, следовательно, можно делить по четыре группы.Избыточность от округленияПример: Кодируются цифры от 0 до 10. Чтобы их представить в виде двоичных, надо 23<10<24 4 бита 1 символ – 4 бита Кодируем блоки по 2 цифры 00 01 … 99 Для передачи информации с помощью двоичной системы 26<99<27 7 бит На 1 символ: 7/ 2 = 3,5 бита Кодируются блоки по 3 цифры 000 210 = 1024, 10 бит информации, следовательно, на один символ: 10/3 = 3,3 бита 001 … 999 Подсчитаем энтропию Н = log n = log 10 = 3,32 бит Чтобы определить избыточность, вызванную округлением, воспользуемся:  где m1 – число символов первичного алфавита; m2 – число символов вторичного алфавита; L – длина кодовой комбинации. , Пример: Передается алфавит из 5 символов: 1, 2, 3, 4, 5, следовательно, m1=5 с помощью двоичных символов 0,1 , следовательно, m2=2. Для передачи сообщения потребуется: 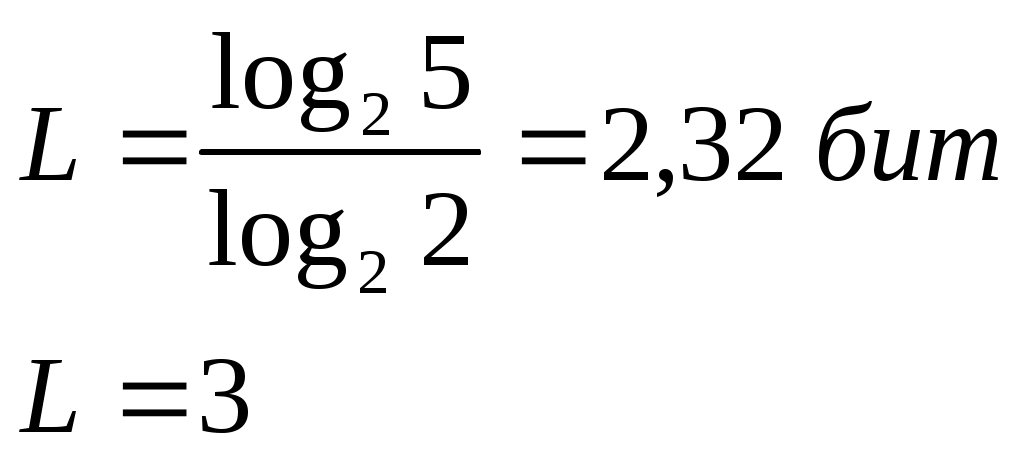 D0 – избыточность от округления  - коэффициент;К – большее целое число. Пример:  Пример: Определить избыточность сообщений от округления при побуквенном и поблочном кодировании, если кодируются цифровые сообщения и передаются в двоичном коде. Кодирование осуществляется блоками по 4, 5, 6 цифр. Первичный алфавит m1=10 Вторичный алфавит m2 = 2 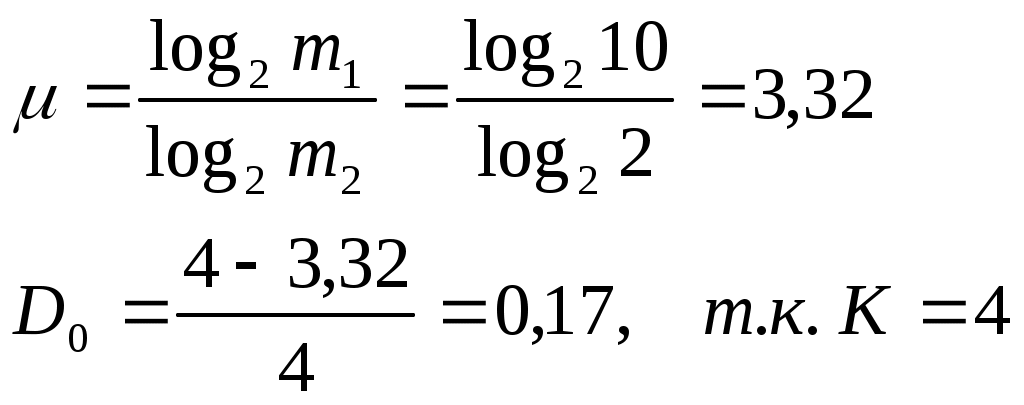 Первичный алфавит из 2-х букв m1=10000 m2=2  Первичный алфавит из блоков по пять m1=100000  Кодируются символы по шесть букв m1=106  , следовательно, этот алфавит наиболее близок к оптимальному. |