теория информации. ТИ (Best). Лекции по предмету "Теория информации" Красноярск 2002

• Название: Лекции по предмету "Теория информации" Красноярск 2002
• Анкор: теория информации
• Дата: 10.12.2022
• Размер: 1.06 Mb.
• Имя файла: ТИ (Best).doc
• Тип: Лекции; #837351
• страница: 10 из 12

Пример: Сообщения передаются в двоичном коде. Время передачи от нуля до одной секунды, r₀ = 1 сек, секунд. Определить скорость передачи информации для случая:

1) Символы равновероятны и независимы.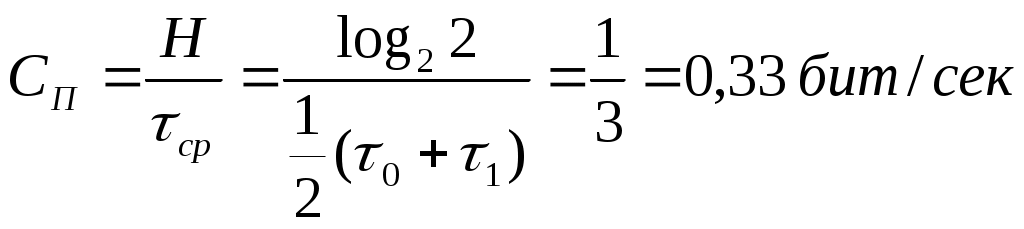



2) Символы неравновероятны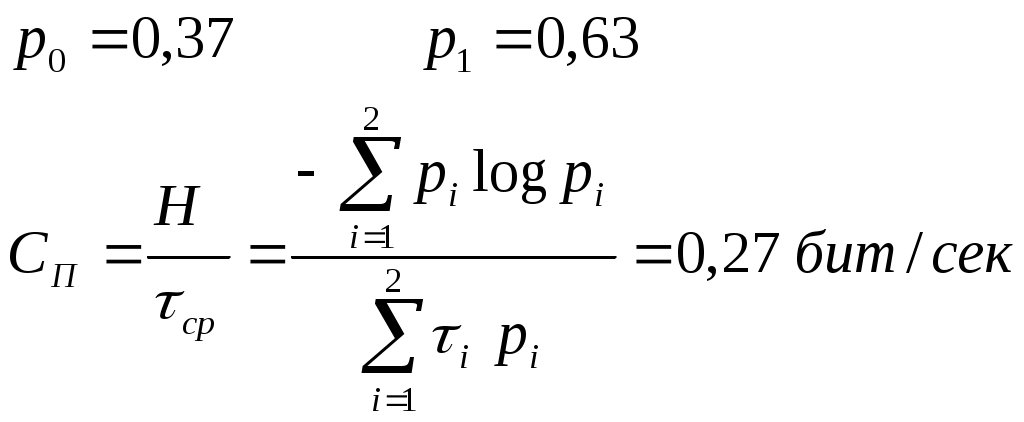

Дискретный канал с помехами
Характеризуется канальной матрицей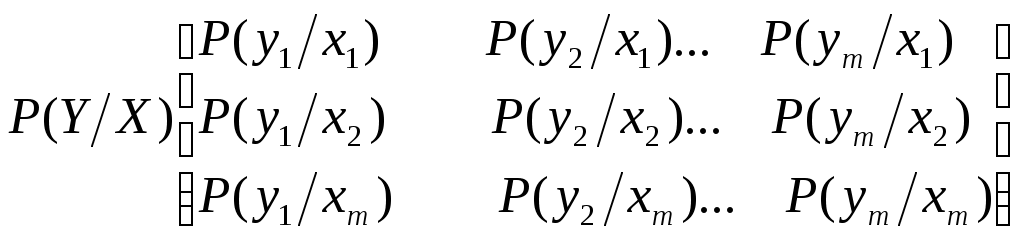


…


Взаимная информация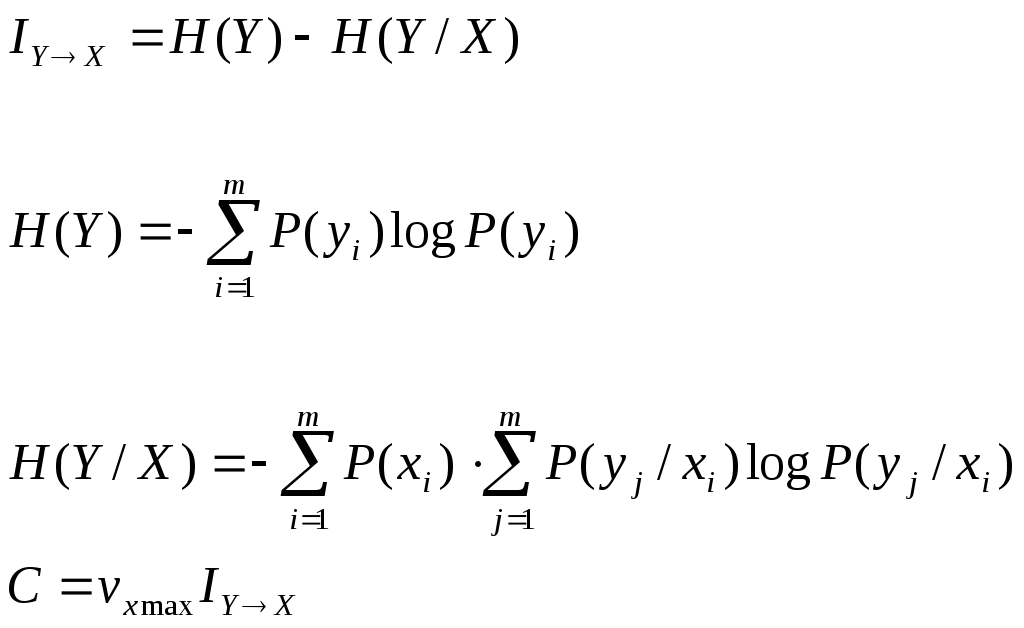


Энтропия на выходе приёмника

Средняя условная энтропия

- это максимальное значение определить сложно.

…

…


Определим пропускную способность канала связи, по которому передаются двоичные сигналы со скоростью v_x, если вероятность искажения сигнала равна p.

Имеет источник информации , приёмник информации .

Разложение выполним в виде диаграммы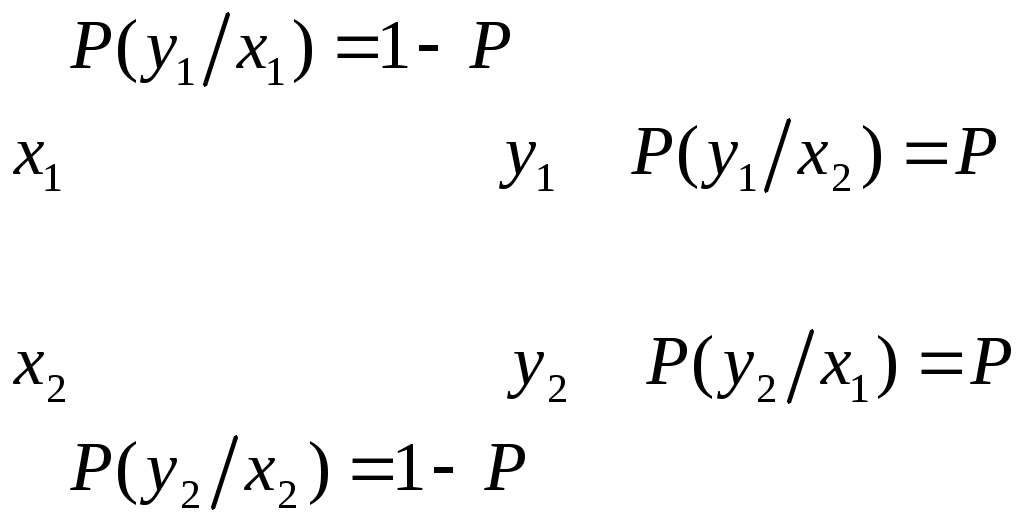


Правильный приём

Канал такого типа называют симметричным бинарным, (т.к. два числа)

Искажение


Определим среднюю условную энтропию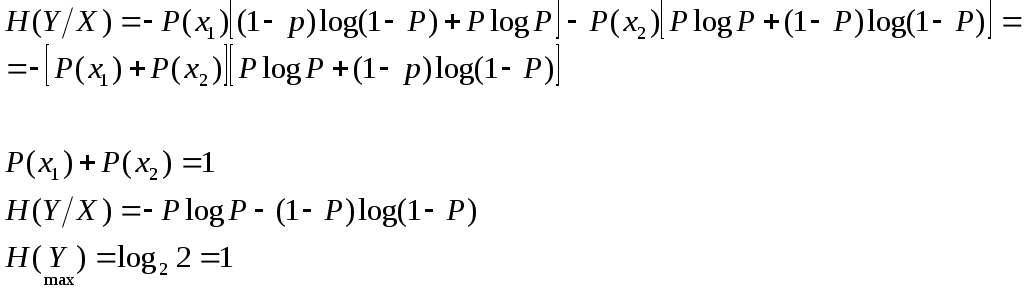


Учитывая, что

, получим, что

 объединили

- , т.е потери не будут зависеть от характерис-тики источника

Поэтому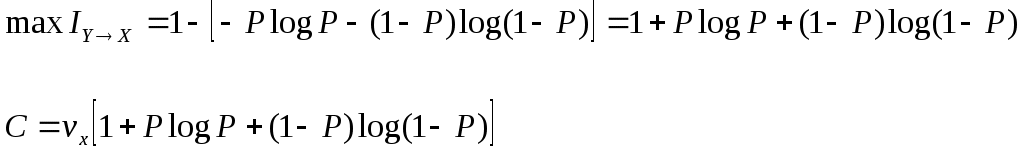


Пропускная способность канала


Рассмотрим два крайних условия:

1. Вероятность искажения (Р=0), следовательно, помех нет, следовательно, С = v_x и она имеет свое максимальное значение

2. Р=1/2. Значение С = 0 – это минимальное значение пропускной способности
Пример: Определить пропускную способность канала связи, способного передавать 100 симв./сек . Каждый символ искажается с вероятностью 0,01.


Теорема о кодировании Шеннона для

дискретного канала с помехами
Если источник информации имеет энтропию H(z), а канал обладает пропускной способностью С, то:

1. Сообщение, вырабатываемое источником, всегда можно закодировать так, чтобы скорость передачи v_z была близка величине v_{z max.}



И чтобы при этом вероятность ошибки в определении переданного символа была меньше заданного числа.

2. Не существует метода кодирования, позволяющего вести передачу со скоростью выше

v_{z max} и с малой вероятностью ошибки.

То есть, если H’(z) ≤ C, то может быть подобран специальный код, позволяющий вести передачу с малой вероятностью ошибки. Если H’(z) > C то такого кода не существует.

Очевидно, что при уменьшении скорости передачи, можно повысить достоверность, например, методом многократного повторения. Для обеспечения нулевой ошибки, кажется, что скорость передачи должна стремиться к нулю. Теорема же утверждает, что всегда можно обеспечить скорость передачи равной V_{z max} путем выбора подходящего ввода.
Корректирующие коды
Это коды, которые позволяют обнаруживать и исправлять ошибки.

n – значность кода (из скольки символов состоит данная кодовая комбинация)
N₀ = 2ⁿ, n – число возможных кодовых комбинаций.

Идея возможности обнаружения ошибок заключается в том, что для передачи используются не все комбинации, а только их часть N.

И это значение N0.

Используемые комбинации N называются разрешенные, а остальные N₀–N – это запрещенные комбинации.

Если в результате действия помех разрешенная комбинация превращается в запрещенную, то это обнаруживает наличие ошибки. Если совокупность ошибок превращает одну разрешенную комбинацию в другую разрешенную комбинацию, то такие ошибки обнаружены не будут.

Примером кода, обнаружившего одиночную ошибку, является коды с контролем по четности. Сущность таких кодов состоит в следующем:

К исходной кодовой комбинации добавляют 1 или 0, таким образом, чтобы количество (сумма) единиц всегда была четной. Сбой любого одного символа обнаружит ошибку.

информационный

контрольный Код 1 00 01 10 11

Код 2 00 01 10 11

0 1 1 0

Чтобы принять сигнал правильно, надо повторить передачу.

Количество символов, на которое одна кодовая комбинация отличающаяся от другой кодовой комбинации, называется кодовым расстоянием и обозначается буквой d. d₀ – минимальное кодовое расстояние – минимальное количество символов, на которое кодовая комбинация отличается друг от друга.

Для того, чтобы определить кодовое расстояние достаточно просуммировать кодовые комбинации по правилам двоичного поля и подсчитать число единиц в полученном результате.
Пример: Для кода 1

А₁ = 00 0  0 = 0 Правила:

А₂ = 01 1  0 = 1 четн. – 0

А₃ = 10 0  1 = 1 нечетн. – 1

А₄ = 11 1  1 = 0

Определим кодовую комбинацию

А₁А₂  d = 1 А₃А₄  d = 1

01 01

Для кода 2

А₁=000 А₂А₄ 011 А₃А₂ 101

А₂=011 110 d = 2 011 d = 2

А₃=101 101 110

А₄=110
Ошибку можно не только обнаружить, но и исправить, если принятая кодовая комбинация ближе к исходной, чем к любой другой разрешённой комбинации.
Пример: Построим код: К коду 2 добавим два символа, повторив первых два символа получим код 3:
Код 2

А₁=000

А₂=011

А₃=101

А₄=110
Код 3

00 01 10 11

000 101 110 011

информационные разряды контрольные разряды

Определим кодовое расстояние между комбинациями

Строим матрицу кодовых расстояний

	А1	А2	А3	А4	d0 = 3
А1	0	3	3	4
А2		0	4	3
А3			0	3
А4				0

Пусть передаётся комбинация А₃, и она содержит ошибку



матрица кодовых расстояний

	А1	А2	А3	А4
Vx	4	3	1	2

v_x ближе всего к А₃, следовательно посылалась А₃ и мы ошибку исправили.

Корректирующая способность кода зависит от минимального кодового расстояния d₀. Если

d₀ = 3, то он может исправлять ошибку, то есть корректирующую способность кода можно повышать, если увеличивать минимальное кодовое расстояние.

Для построения кодов, которые обнаруживают и исправляют одиночную ошибку d₀ = 3, должно выполняться неравенство:

, где

n_и – количество информационных разрядов

n – значность кода

n_к – количество контрольных разрядов

n = n_и + n_к
Поэтому результаты сведем в таблицу:

n	5	6	7	8	9	10	11	12	13	14	15
nи	2	3	4	4	5	6	7	8	9	10	11
nк	3	3	3	4	4	4	4	4	4	4	4

Предположим, что строим код на тридцать два сообщения n_и = 5, выделяем столбец

n_к = 4

n = 9
Расчеты можно вести по формуле.

Для кода, который обнаруживает двойную ошибку, а исправляет одиночную:

- значения округляются в большую сторону

- до большего целого числа
Обозначим буквой:

r – кратность обнаруживающих ошибок;

s – кратность исправляемых ошибок;

Тогда для кодов обнаруживающих и исправляющих ошибки:

d₀ = r + s + 1,

для кодов, которые только обнаруживают ошибки d₀ = n + 1,

для кодов, которые только исправляют ошибки d₀ = 2s + 1 (когда r > s).

Если

d₀ r s

1 0 0 отличие комбинации

2 1 0 обнаружение одиночной ошибки

3 1 1 обнаружение одиночной ошибки и исправление одиночной ошибки

3 2 0 обнаруживающий 2-ую ошибку
Количество контрольных разрядов и значность кода для разных минимальных кодовых расстояний, связано соотношением:

Для кодов, обнаруживающих все трехкратные ошибки.



количество обнаруженных ошибок

Для кодов, исправляющих двойные ошибки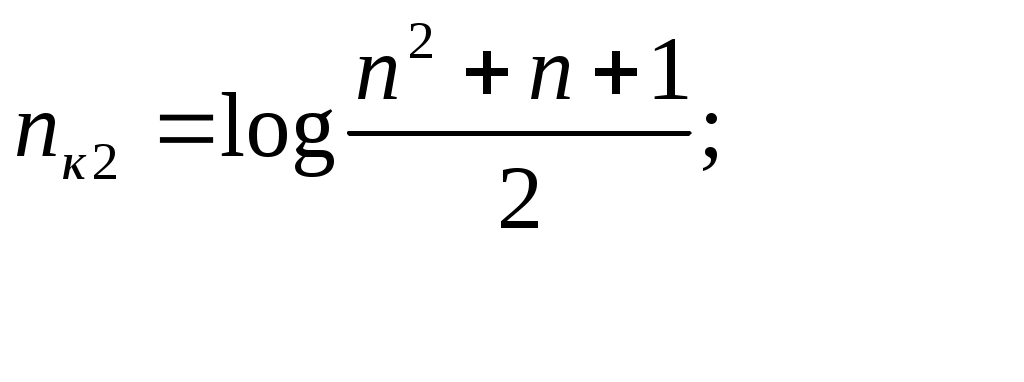



Для кодов, исправляющих тройные ошибки:



Для кодов, исправляющих S ошибок:


Пример: Требуется передавать, обнаруживающим трёхкратные ошибки, все комбинации пятизначного двоичного кода. Чему равна общая длина кода ?
r – кратность обнаруживающих ошибок.

s – кратность исправляемых ошибок.


n_и = 5; n_к = 1 + log[6 + log6] = 5

n = n_и + n_к = 10
Пример: Определить количество информационных разрядов кода длиной в пятнадцать символов, если код исправляет две ошибки.

n=15



n_и = n - n_к = 15 – 7 = 8
Исправление ошибок с помощью полной

кодовой таблицы
Процесс исправления ошибок поясняется с помощью диаграммы.

A_k – разрешённые комбинации B_j – запрещённые комбинации
А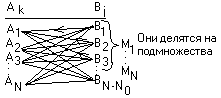
₁ может искажена и может превратиться в B₁ или B₂ и т.д. в любую из запрещённых комбинаций. Запрещённые комбинации делятся на подмножества H_k.

Способ приема состоит в том, что если принимается комбинация B_j, которая попадает в подмножество М_к, то считается, что принята комбинация А_к (M₁ соответствует тому, что передавалась комбинация A₁).

Исправляющая способность кода будет зависеть от выбора разбиения или от стратегии.
Пример: Рассмотрим пример построения КУ. Пусть l_i – вектор ошибки, он имеет те же размерность, что и кодовая комбинация. 1 – искажения есть, 0 - искажений нет. Пусть кодируется набор из 4-х комбинаций.
А₁=0001

А₂=0101

А₃=1110

А₄=1111

Bj=А_к+l_i

li	Ак				q
	0001	0101	1110	1111	1
0001 0010 0100 1000	0000 0011 - 1001	0100 0111 - 1101	- 1100 1010 0110	- 1101 1011 0111
0011 0101 1001 0110 1010 1100	0010 0100 1000 0111 1011 1101	0110 0000 1100 0011 - 1001	1101 1011 0111 1000 0100 0011	1100 1010 0110 1001 - 0011	2
0111 1011 1101 1110	0110 1010 1100 -	0010 - 1000 1011	1001 - 0011 0000	1000 0100 0010 -	3
1111	-	1010	-	0000	4

Разбиение
Разбиение запрещенных кодовых комбинаций на множества зависит от статистики ошибок и выбранной стратегии. Если ошибки в каждом символе независимы, то вероятность ошибок убывает с повышением ее кратности. Для уменьшения средней вероятности ошибки следует в начале исправлять ошибки меньшей кратности.

На практике действуют следующим образом: оставляют комбинации в сроках с низшей кратностью и вычеркивают одинаковые комбинации в строках с высшей кратностью. Действуя, таким образом получают таблицу комбинаций:

М1	М2	М3	М4	q
0000 0011 1001	0100 0111 -	1100 1010 0110	1101 1011 -	1
0010	-	1000	-	2

Т.е. Исправили десять одинарных и две двойные ошибки.

Если статистика ошибок такова, что большую вероятность имеют ошибки высшей кратности, то разбиение изменяют: оставляют комбинации в строках с высшей кратностью и вычеркивают в строках с низшей.

“-“ значит действие помехи переходит в разрешенную комбинацию и мы ее обнаруживаем.

М1	М2	М3	М4	q
1101	-	0111	-	2
0110 1100	1000 1011	0001 0011	0100 0010	3
-	1010	-	0000	4

Если статистика ошибок такова, что какая-нибудь комбинация искажается больше, чем другие, например, комбинация А₁, то стратегия разбиения будет другая: оставляем все кодовые комбинации соответствующие А₁, т.е. М₁, а остальные вычеркиваем: комбинации, которые не совпадают, остаются

А1 М1	А2 М2	А3 М3	А4 М4	q
0000 0011 1001	- - -	1100 0010 0110		1
0010 0100 1000 0111 1011 1101				2

Систематические коды
Это коды, в которых контрольные и информационные разряды размещаются по определенной системе. Закономерности, заложенные в структуре этих кодов, позволяют проводить декодирование более простым способом, чем методом полной кодовой таблийы.

Кодовый вектор – последовательность 0-й и 1-й кодовой комбинации.

Вес кодового вектора – число единиц в кодовой комбинации.

Нулевой вектор – кодовая комбинация, состоящая из одних нулей.
n – значность кода (из скольки символов состоит кодовая комбинация);

n_u – число информационных разрядов;

n_k – число контрольных разрядов;
Пример: Для систематических кодов применяют обозначение:

Код(n, n_u) Код (5,3)
Построение систематических кодов производится следующим образом: в качестве первого берется нулевой вектор, затем составляется производящая матрица. Она имеет n_и – строк, n – столбцов. В качестве строк производящей матрицы берутся любые линейно независимые n-значные векторы, отстоящие друг от друга не менее, чем на заданное кодовое расстояние. Строки матрицы G – являются кодовыми векторами. Первый вектор - нулевой.

Линейно независимыми называются векторы, для которых выполняется условие:

v₁, v₂,...,v_к

v₁ + v₂ + ...+ v_к ≠ 0
Остальные кодовые векторы определяются количеством:

где

- всего (общее число кодовых векторов);

- находится в производящей матрице;

1 –нулевой вектор.
Остальные кодовые векторы получаются в результате суммирования строк производящей матрицы G в различных сочетаниях.

Для обнаружения ошибок составляется множество проверочных векторов, ортогональных векторам кода. Т.е. если кодовый вектор v образован символами а₁, а₂,…, а_n, а ортогональный вектор u образован символами – b₁, b₂,..., b_n, то



Из векторов u составляется проверочная матрица Н. Она имеет n_к – строк, n-столбцов. Строками матрицы Н являются любые линейно-независимые векторы u.
Пример: Пусть строится код (5,3) с минимальным кодовым расстоянием d₀=2. Он позволяет обнаруживать все одиночные ошибки. Составим производящую матрицу G:

Три строки, т.к. n_u = 3, n = 5 – столбцы

Комбинации Результат комбинации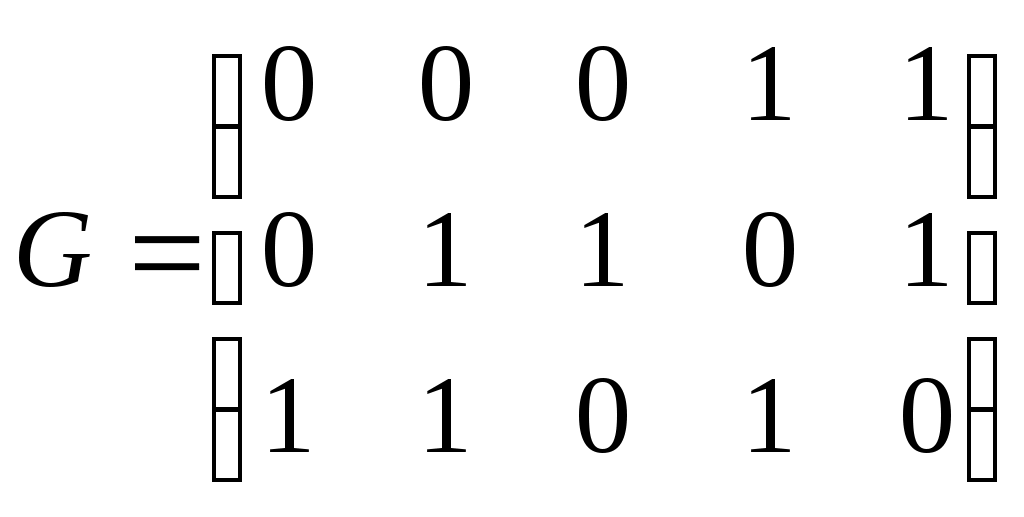


Нулевой вектор

Строки матрицы

G

1 + 2

2 + 3

1 + 3

1 + 2 + 3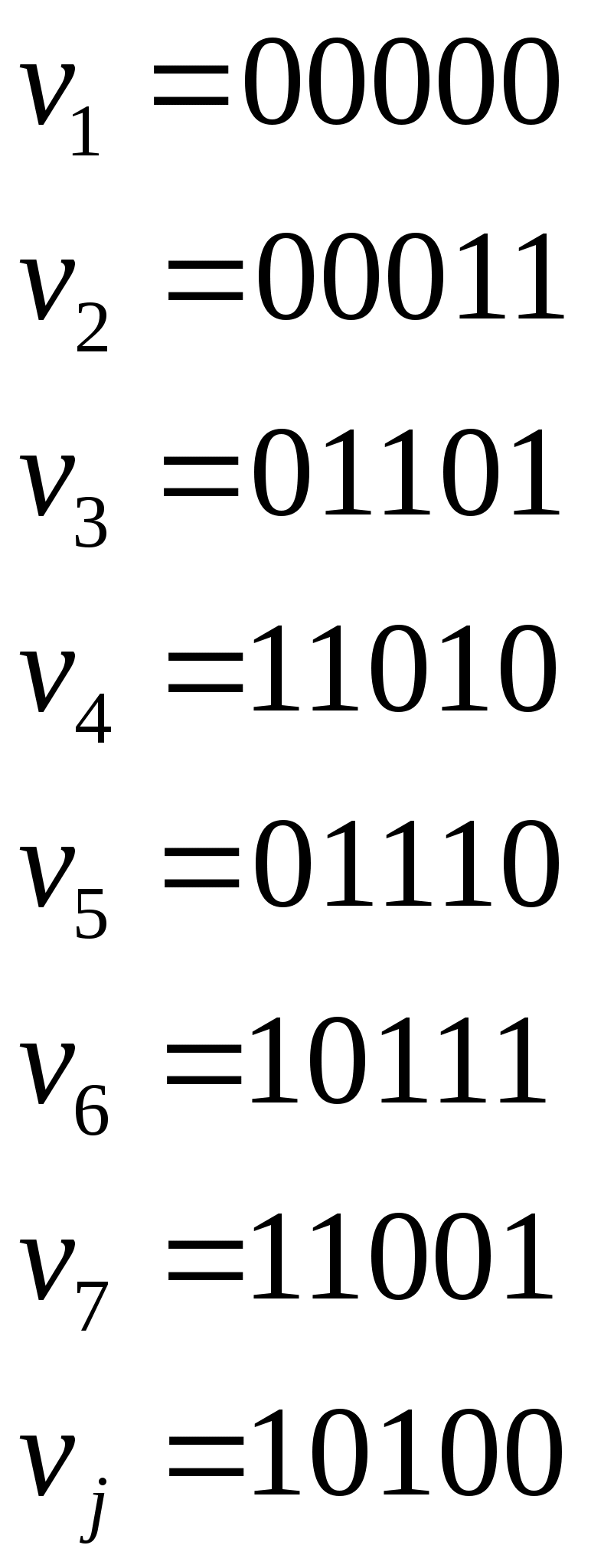

Можно было бы построить G из любой другой тройки векторов, кроме сочетаний v₂v₃v₅, v₂v₄,v₁ и т.д. (семь штук), т.к. эти сочетания линейно зависимы, т.е. v₂ + v₄ + v₇ ≠0.

Построим ортогональные векторы u (проверочные).

Составим для векторов v₂, v₃, v_8. Эти вектора имеют минимальное количество единиц.

v₂ 0  b₁ + 0  b₂ + 0  b₃ + 1  b₄ + 1  b₅ = 0

b₄ + b₅ = 0

v₃ b₂ + b₃ + b₅ = 0

v₈ b₁ + b₃ = 0
Для любого вектора u должно выполняться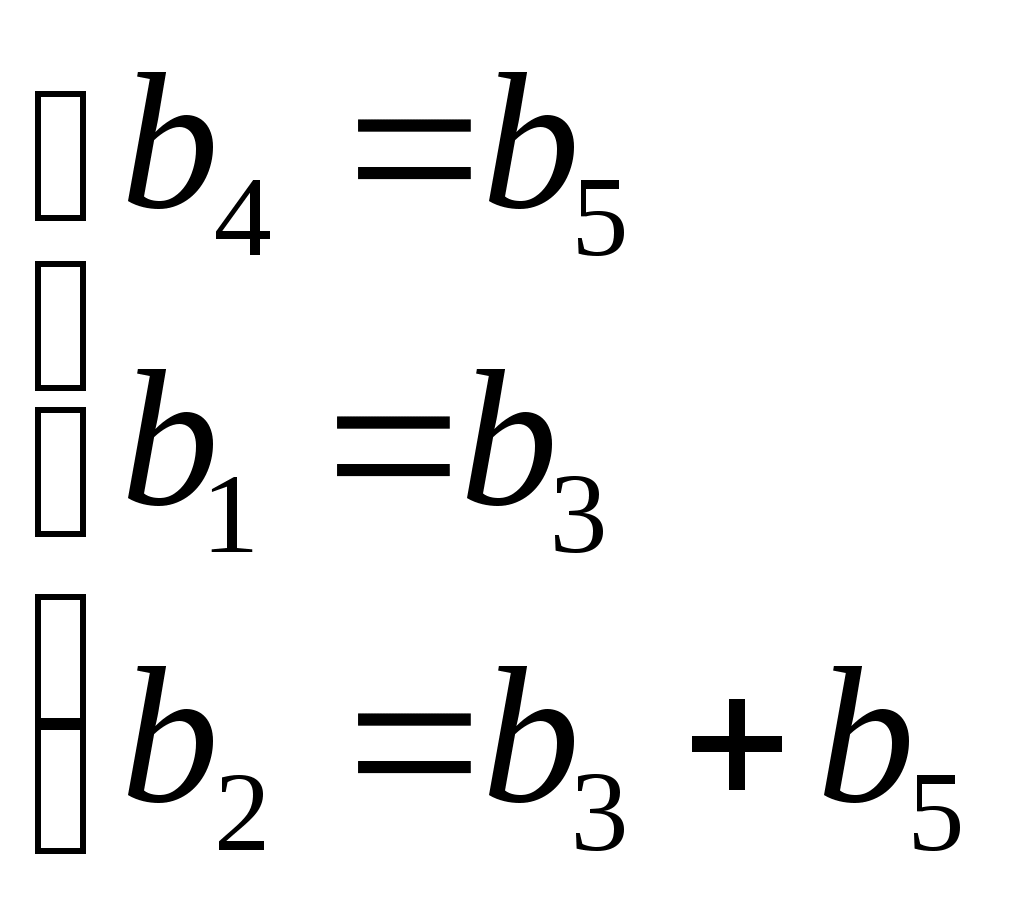


Перебирая все удовлетворяющие этим условия сочетания, получили:

u₁ = 00000

u₂ = 01011

u₃ = 10111

u₄ = 11100
Из этих векторов необходимо составить проверочную матрицу Н

- т.к. они линейно независимы
Декодирование систематических кодов
1. Декодирование с помощью полной кодовой таблицы. Рассчитаем параметры этой таблицы
N = 2⁵ = 32 – код пяти значений

N₀ = 2³ = 8 – разрешённая комбинаяция

N - N₀=32-8=24 – запрещённая коибинация ( кодовых исправлений 24 ошибки )
Строим полную кодовую таблицу. В качестве первой строки используем разрешенные комбинации v₁ – v₈

00000	00011	01101	11010 01110 10111 11001 10100
00001 00100 01000	00010 00111 01011	01100 01001 00101	…

Общий метод декодирования состоит в следующем: Приняв некий вектор v_x, содержащий ошибку, его отыскивают в полной кодовой таблице и соотносят с тем кодовым вектором, который стоит в верхней строке этого столбца.

Пример: v_x=00111, находим в таблице и соотносят с 01 строкой, т.е. v = 00011
Достоинство метода: его универсальность, возможность применять различные стратегии.
Недостаток: громоздкость кода и только 3-и ошибки.
2. Декодирование с проверкой на четность.
С помощью ортогональных векторов u из матрицы Н можно установить связь между составляющими векторов v.
Используя условие ортогональности:



Составляющие 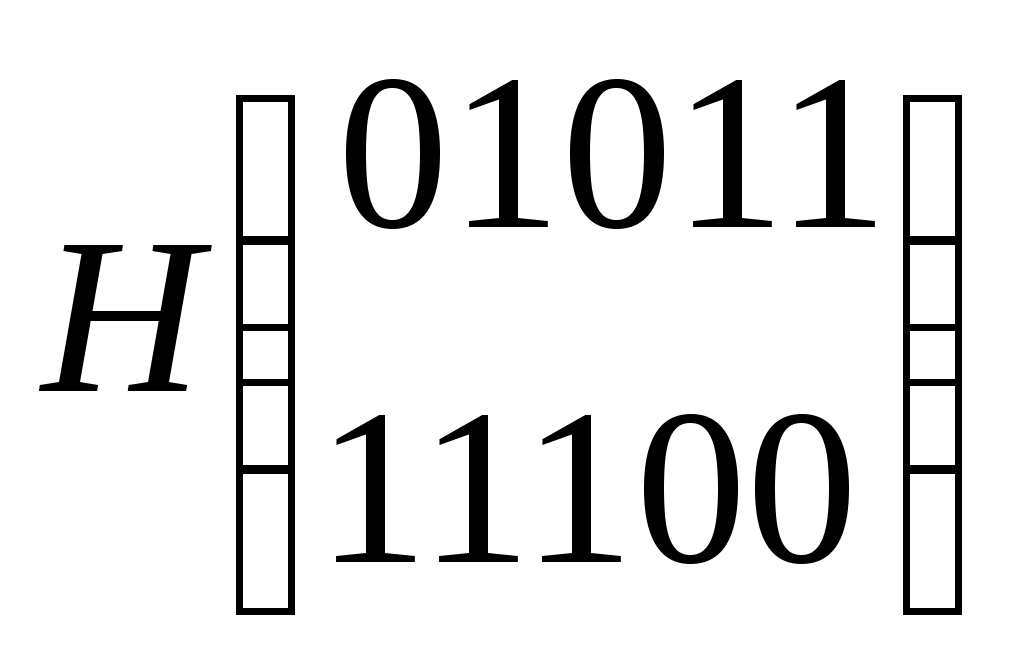- берутся из матрицы Н, а - из принятого вектора.

схема проверок:

На основании векторов u можно записать схему проверок



Пример: , пусть принят вектор v_x = 00110. Он имеет координаты а₁ а₂ а₃ а₄ а_5. Составим схему проверок.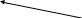



Если бы ошибок не было бы, то здесь были бы нули.
Возможность кода к исправлению ошибки можно объяснить схемой

	N символов
N-проверки	1	2	3	4	5
1		+		+	+
1	+	+	+

Следовательно, данный код может исправить во втором бите, обнаружить ошибку четвёртом или пятом бите, обнаружить ошибку в первом и третьем бите.

Для исправления всех ошибок надо, чтобы каждый бит появлялся в оригинальной комбинации строк в таблице проверки, и так будет, когда d₀=3 и добавиться ещё одна проверка.

3. 
   Декодирование с помощью корректирующего вектора
   

Составляется корректирующий вектор, принятая кодовая комбинация умножается на корректирующий вектор, если принятая комбинация без ошибок, то корректирующий вектор равен нулю (т.е. результат умножается).Если есть ошибка, то результат ненулевой, каждой ошибке ставится в соответствие свой ненулевой результат умножения.

Составляющие вектора С c₁,c₂,..,c_i представляют собой скалярное произведение принятого вектора v_x на строки исправляющей матрицы . Вектор представляется двоичным числом С = c₁,c₂,…,c_к. Если ошибок нет, то С = 0
Рассмотрим i-ую строку полной кодовой таблицы

- i-ая строка полная кодовая таблица
Умножим эту строку на вектор u_j, то получим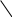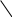



=0 =0 =0
- в каждой строке будет одной и той же величиной для любой кодовой комбинации.

Метод декодирования состоит из следующих операций:

1. 
   По полной кодовой таблице и матрицы Н вычисляют корректирующий вектор С;
   
2. 
   Принятый вектор v_x умножают на векторы матрицы Н и вычисляют корректирующий вектор.
   
3. 
   Сравнивают полученные значения корректирующего вектора с имеющимся шаблоном и определяют ошибку
   

Пример: Нужно выбрать систему кодирования. Возьмём ту же систему кодов и H.

1. Определение шаблонов корректирующего вектора

Векторы ошибок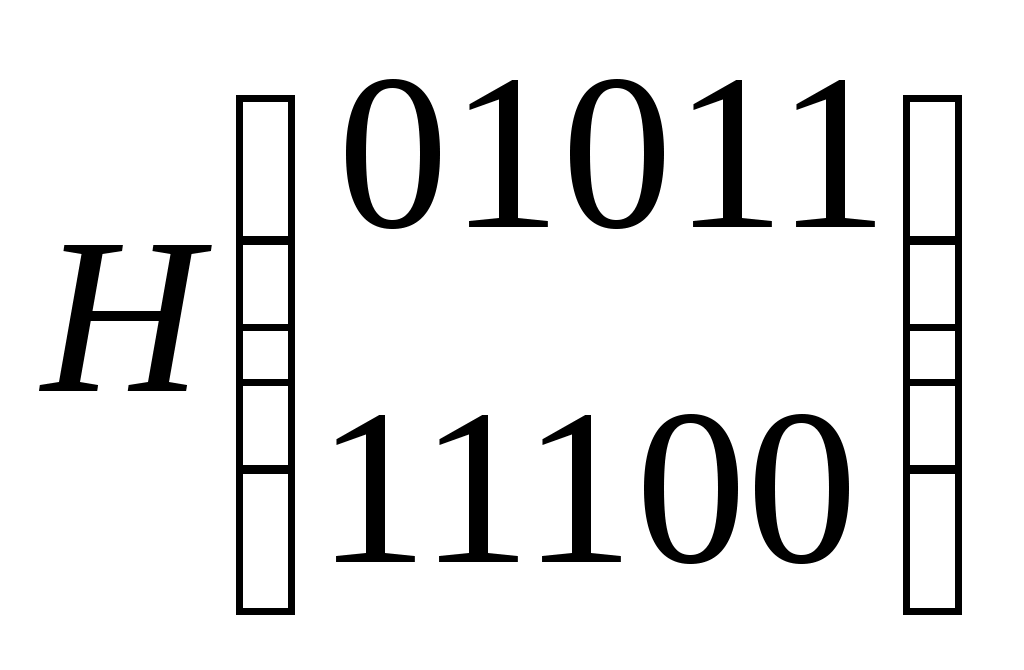


шаблоны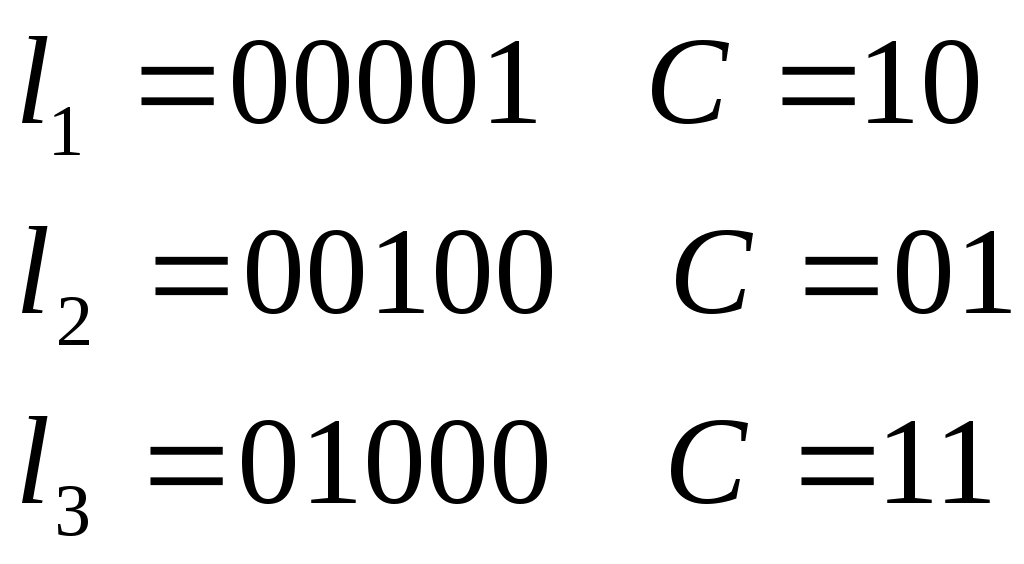


Для вектора e₁ построение шаблона.

e₁:

e₁u₁ = 0000101011 = 1  C₁ = 1

e₁u₂ = 0000111100 = 0  C₂ = 0

Следовательно, вектору e₁ ставится в соответствие вектор С = (10)

Для e₂:

e₂u₁ = 0010001011 = 0  C₁ = 0

e₂u₂ = 0010011100 = 1  C₂ = 1

Для e₃:

e₃u₁ = 0100001011 = 1  C₁ = 1

e₃u₂ = 0100011100 = 1  C₂ = 1
Шаблоны известны на приёмной стороне ещё до посылки комбинации
2. Определение корректирующего вектора
Пусть принят вектор v_x = 01001


Сравниваем полученный вектор ошибки с нашим шаблоном и определяем, что это e₂.
3) Исправляем ошибку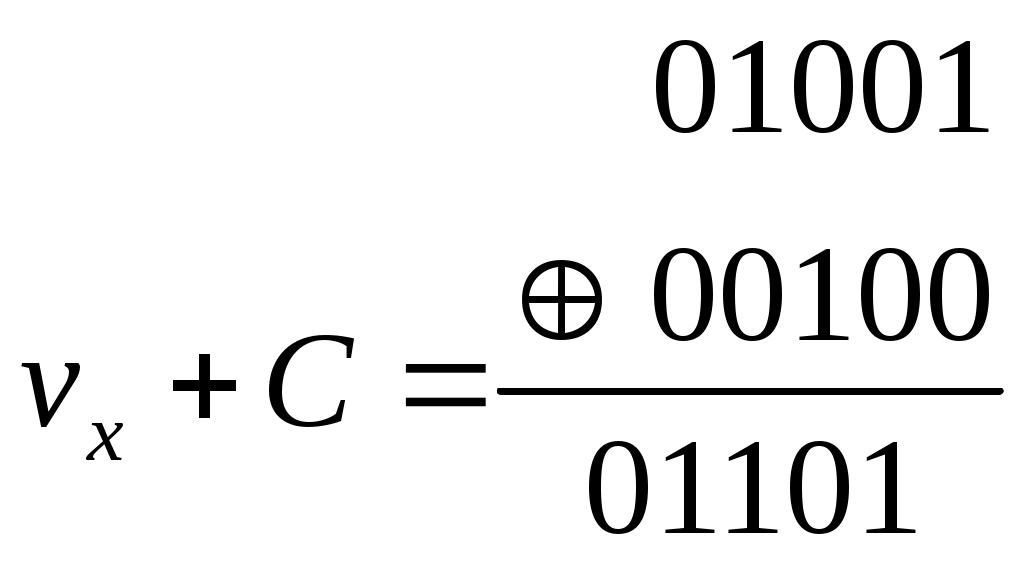

, что соответствует комбинации v₃.

Можно строить образующую матрицу достаточно простым способом, например, единичной матрицей n_u  n_i.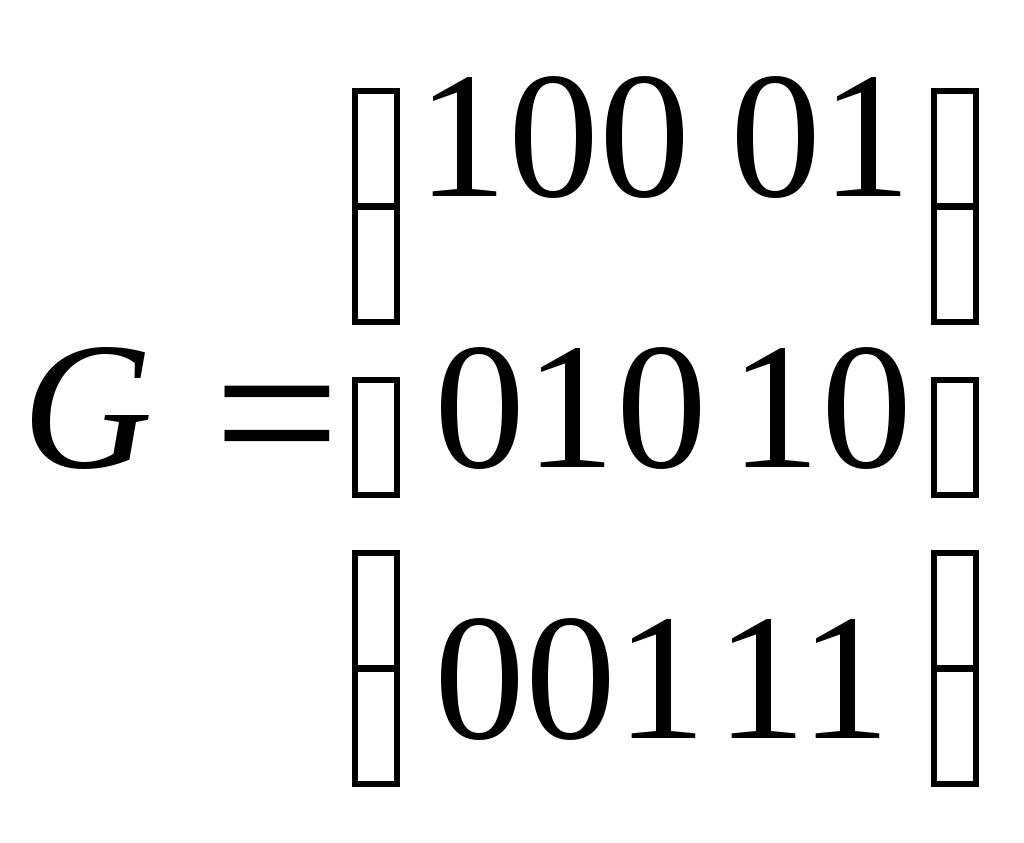

Эта матрица порождает восемь кодов, которые также позволяют обнаружить одиночную ошибку.

Преимущество кода состоит в том, что его можно легко составить, в исправляющих способностях выйгрыша нет.