теория информации. ТИ (Best). Лекции по предмету "Теория информации" Красноярск 2002

• Название: Лекции по предмету "Теория информации" Красноярск 2002
• Анкор: теория информации
• Дата: 10.12.2022
• Размер: 1.06 Mb.
• Имя файла: ТИ (Best).doc
• Тип: Лекции; #837351
• страница: 6 из 12

Частная информация о системе

Пусть имеется две системы X и Y и они взаимосвязаны. Определим частную информацию о системе X, содержащуюся в отдельном сообщении.



По теореме умножения вероятностей:

p_i,j = r_j * p(x_i / y_j) – подставим в
;
Частная информация как и полная, не может быть отрицательной величиной. Для вычисления частной информации через совместные вероятности используют преобразования.
, тогда
Пример: Система X и Y характеризуется таблицей вероятностей.

Определить частную информацию о системе х, содержащуюся в сообщении y1. xi & yi	x1	x2	rj
y1	0.1	0.2	0.3
y2	0.3	0.4	0.7
pi	0.4	0.6

бит
Частная информация о событии, получаемая в результате сообщения о другом событии.

Если вероятность события p_i увеличивает вероятность, т.е. p(x_i, y_j) больше p_i, то информация больше нуля ( ). В противном случае, информация .
Энтропия и информация для систем с непрерывным множеством состояний
Существуют непрерывные системы. Например, время безотказной работы прибора, координаты точки попадания при выстреле.

Рассмотрим систему х, которая определяется непрерывной случайной величиной х с плотностью распределения f(x).

Определим энтропию системы. Заменим непрерывную кривую f(x) ступенчатой.

Площади прямоугольников f(x_i)*x – вероятности попадания в них случайных величин.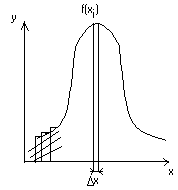





Энтропия системы: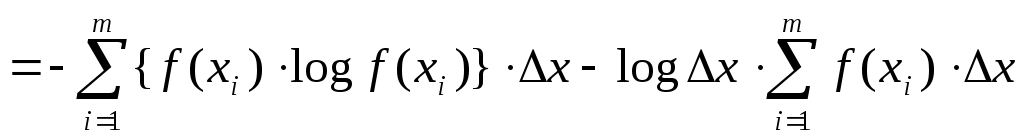





При достаточно малых сумму можно заменить интегралами

, т.к. интеграл вероятностей, следовательно

- энтропия непрерывной системы

Когда величина , особый случай. В этом случае и , т.е. чем выше точность определения состояния системы, тем выше неопределённость (H(x)).

- приведённая энтропия

Условная энтропия непрерывной системы
Пусть имеется две системы: X и Y, они взаимозависимы и непрерывны.

f(x, y) – плотность распределения для состояния определнной системы.

f₁(x) – плотность распределения системы X.

f₂(y) – плотность распределения системы Y.

f(y/x), f(x/y) – условная плотность распределения. Имея эти плотности, можно определить

условную энтропию.
Частная условная энтропия



Полная средняя условная энтропия получившаяся в результате осреднения



Для непрерывных систем – энтропия совместимых систем равна сумме энтропий.
H(x, y) = H(x) + H(y / x)
Пример: Найти энтропию непрерывной системы X, все состояния которой на участке от 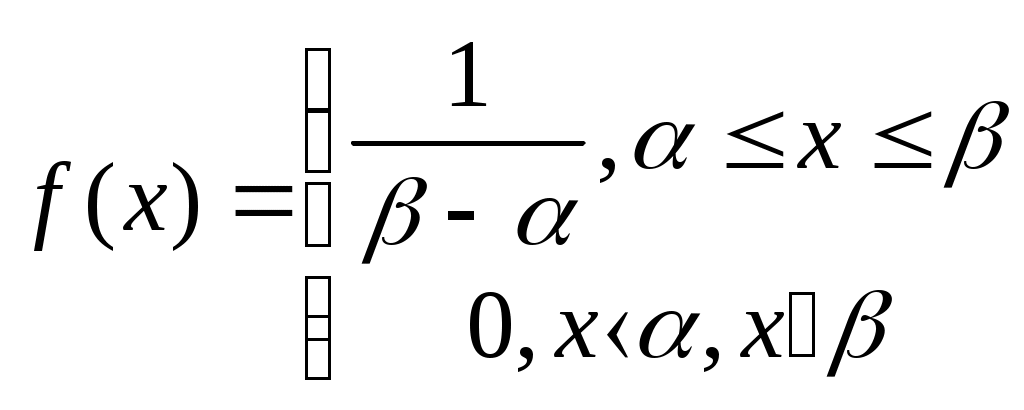до равновероятны.


H^* = =

Пример: Для нормального закона распределения.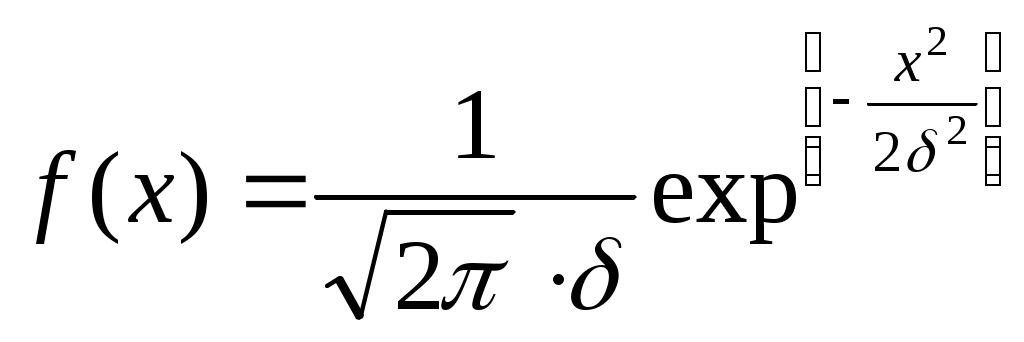

H(x) =

Подставляем f(x) и log в интеграл, получим после вычисления



Проводимые исследования различных законов распределения показали, что наилучшим законом распределения является равномерный закон. Если накладываются ограничения - мощность сигнала равная постоянной величине, - наилучшим законом распределения является нормальный.