теория информации. ТИ (Best). Лекции по предмету "Теория информации" Красноярск 2002

• Название: Лекции по предмету "Теория информации" Красноярск 2002
• Анкор: теория информации
• Дата: 10.12.2022
• Размер: 1.06 Mb.
• Имя файла: ТИ (Best).doc
• Тип: Лекции; #837351
• страница: 12 из 12

Декодирование кода Хэминга

В процессе декодирования производится проверка на чётность по схеме проверок и строится вектор ошибок S(S_k, …,S₁). Если проверочная сумма равна нулю, то в вектор ошибки записывается ноль иначе записывается единица. Всего делается n_k проверок. В результате первой проверки определяется составляющая S₁, последней составляющая S_k. Если принятая кодовая комбинация содержит ошибку, то в векторе S образуется число, которое указывает номер ошибочной позиции.


a₁a₂a₃a₄a₅a₆a₇


Пример: Послана комбинация v_k = 0100101. Принятая комбинация v_x = 0100111, т.е. имеется ошибка в шестом разряде Составим схему проверок.
1) a₁ + a₃ + a₅ + a₇ = 0 + 0 + 1 + 1 = 0  S₁ = 0

2) a₂ + a₃ + a₆ + a₇ = 1 + 0 + 1 + 1 = 1  S₂ = 1

3) a₁ + a₅ + a₆ + a₇ = 0 + 1 + 1 + 1 = 1  S₃ = 1
S = 110  это двоичное число шесть, что соответствует разряду a₆, следовательно, ошибка в шестом разряде.

Для исправления одинарной и обнаружение двойной ошибки, кроме проверок по контрольным позициям проводят проверку на чётность для каждого кода. Для этого при формировании кода каждому коду в конце кодовой комбинации добавляется контрольный символ так, чтобы сумма единиц в полученной комбинации всегда была чётной.
Особенности декодирования.
При наличии одной ошибки проверкой на чётность можно обнаружить ошибку. Проверки по позициям укажут номер ошибочной позиции. При наличии двойной ошибки, проверка на чётность не фиксирует ошибку. Проверки по позициям укажут наличие ошибки.
Пример: Построить код Хэминга для исправления одиночной и обнаружения двойной ошибки четырёх значного двоичного кода.

0001 n_u = 4 n_k = 3
Макет кода

а₁а₂а₃а₄а₅а₆а₇

k₁k₂0k₃001k₄
Схема проверок:

1) a₁ + a₃ + a₅ + a₇ = k₁ + 0 + 0 + 1 = 0  k₁ = 1

2) a₂ + a₃ + a₆ + a₇ = k₂ + 0 + 0 + 1 = 0  k₂ = 1

3) a₁ + a₅ + a₆ + a₇ = k₃ + 0 + 0 + 1 = 0  k₃ = 1


11010010

1101001k₄ Количество единиц чётное, следовательно сам код
Рассмотрим пример для v_k = 01001011. Пример обнаружения единичной ошибки.


a₁a₂a₃a₄a₅a₆a₇


v_k = 01001011  ошибка в четвёртом разряде

v_x = 01011011

1. 
   Проведим проверки на чётность, которые указывают наличие одиночной ошибки.
   
2. 
   Проведим проверку по позициям.
   

Составляем схему проверок

1) a₁ + a₃ + a₅ + a₇ = 0 + 0 + 1 + 1 = 0  s₁ = 0

2) a₂ + a₃ + a₆ + a₇ = 1 + 0 + 0 + 1 = 0  s₂ = 0  S = (001)  a₄

3) a₁ + a₅ + a₆ + a₇ = 1 + 1 + 0 + 1 = 1  s₄ = 1
Пример: Обнаружение двойной ошибки.
V_k = 01001011

V_x = 11011011

1. 
   Делаем проверку на чётность, число единиц чётное, следовательно, проверка ошибки не обнаруживает.
   
2. 
   Делаем проверки по позициям
   

Схема

1) a₁ + a₃ + a₅ + a₇ = 1 + 0 + 1 + 1 = 1  s₁ = 1

2) a₂ + a₃ + a₆ + a₇ = 1 + 0 + 0 + 1 = 0  s₂ = 0  S = (101)

3) a₁ + a₅ + a₆ + a₇ = 1 + 1 + 0 + 1 = 1  s₃ = 1
В этом случае S не указывает разряд ошибки, но S просто показывает, что она есть.
Циклические коды
Циклические коды названы так, потому что у них часть комбинаций может быть получена путём сдвига одной или нескольких комбинаций. Для проверки и обнаружения ошибок используется операции циклического сдвига. Циклические коды относятся к числу систематических кодов.

Идея построения циклических кодов базируется на использовании неприводимых в поле двоичных чисел многочленов.

Не приводимыми называют многочлены, которые делятся без остатка на себя и на единицу. Под полем двоичных чисел подразумевается, что все операции проводятся по правилам сложения (и т.д.) двоичных чисел. Неприводимые многочлены играют роль производящих многочленов. Если информацию кодовой комбинации умножить на выбранный неприводимый многочлен, то получим циклический код. Корректирующая способность кода будет определяться видом неприводимого многочлена. В теории циклических кодов, кодовые векторы принято представлять в виде полиномов.

x³x²x¹x⁰

Например: u(x) = x³ + x² +1  1 1 0 1
Построим циклический код. Образующий многочлен к(х) = х³ + х + 1 = 1011. При построении циклических кодов существует несколько приёмов.

1. Умножим кодовый вектор u(x) на одночлен той же степени, что и образующий многочлен.

u 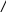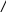(x) * xⁿ = (x³ + x² + 1) * x³ = x⁶ + x⁵ + x³ = 1101000

инф.. корректирующие разряды

часть

Чтобы уточнить значения корректирующих разрядов производят деление . Делить можно используя полиномы и значения двоичных разрядов.
Разделим один многочлен на другой

1 101 000 1011  001

1 011 1101001

1100

1011

1110

1011

1010

1011

001  остаток от деления - он прибавляется к исходной комбинации
1101000

+ 001

1101001 - искомый циклический код
В общем виде можно записать

, где Q(x) – частное; K(x) – остаток

Умножим левую и правую часть k(x) и получим:

u(x) * xⁿ = Q(x) * K(x) + R(x)

u(x) * xⁿ + R(x) = Q(x) * K(x) – знак перед R(x) не имеет значение

= F(x) – это цикловой код.
Т.о. получается дваспособа образования циклического кода:

1) Путём умножения одной из комбинаций информационной части кода на образующий многочлен:

Q(x) * K(x) = I(x)
2) Умножение заданной комбинации на одночлен и той же степени, что и выбранный образующий многочлен с добалением остатка от деления.

Эти способы являются теоретическим основанием для построения кодирующих и декодирующих устройств.

Образующий многочлен K(x) принимает участие в образовании в каждой кодовой комбинации. Поэтому любой многочлен циклического кода делится на образующий без остатка. Если при делении обнаружен остаток, значит принятая комбинация содержит ошибку.

Для построении циклических кодов обычно используют образующую матрицу.
Способы построения образующей матрицы:

Первый способ

1) Образующая матрица получатся как результат слияния двух матриц: Первая - единичная повёрнутая размером n_u.
n_u = 4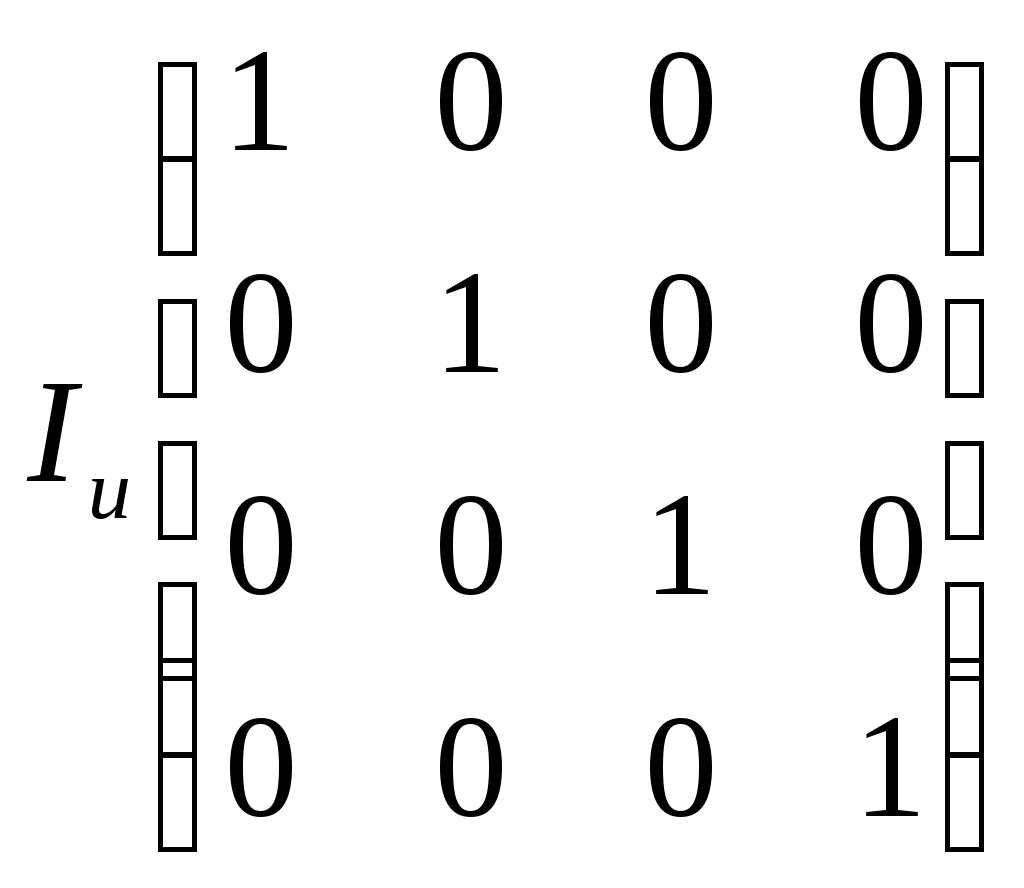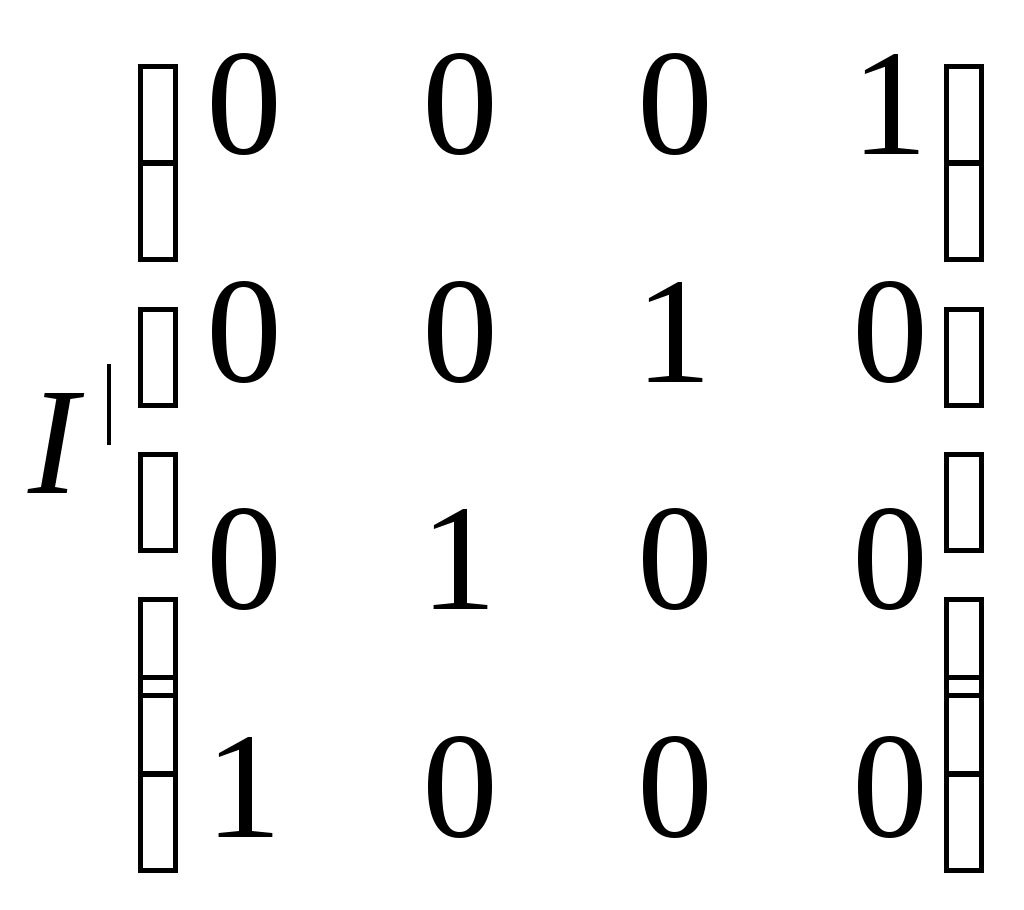
Дополнительная матрица имеет n_u – строк и n_k – столбцов. Для определения строк дополнительной матрицы используют результаты делений последней строки первой повёрнутой матрицы на образующий многочлен.
1 0000 … k(x)




В качестве строк дополнительной матрицы используются остатки от деления.
Пример: k(x) = 1011

Рассмотрим процедуру деления
1
Остаток

011

110

111

101

001

010

100

00000… 1011

1011

01100

1011

1110

1011

1010

1011

001000

1011




В дополнительной матрице используются лишь те остатки, вес которых W = d₀ – 1. d₀ – минимальное кодовое расстояние. Строки образующей матрицы представляют собой первые комбинации искомого кода. Остальные комбинации получают суммированием различных сочетаниям строк.
Второй способ

Образующая матрица может быть построена в результате умножения элементов единичной матрицы размером n_u на образующий многочлен.
Третий способ

Образующая матрица может быть получена в результате циклического сдвига любой комбинации, полученной по способу два.
Декодирование циклических кодов
Остатки от деления полученного вектора на образующий многочлен является опознавательным. Идея обнаружения ошибки заключается в следующем принятая кодовая комбинация делится на образующий многочлен. Если есть остаток, то производится циклический сдвиг принятой кодовой комбинации. Затем сдвинутая комбинация снова делится на образующий многочлен. После ряда циклических сдвигов определяется такое положение, при котором остаток минимален.
Таблица неприводимых двоичных многочленов

Код	Многочлен	Код	Многочлен
11	x + 1	10001	x4 + 1
101	x2 + 1	10011	x4 + x + 1
111	x2 + x +1	10101	x4 + x2 +1
1001	x3 + 1	10111	x4 + x2 +x + 1
1011	x3 + x +1	11001	x4 + x3 + 1
1101	x3 + x2 + 1	11011	x4 + x3 + x + 1
1111	x3 + x2 + x + 1	11101	x4 + x3 + x3 +1
		11111	x4 + x3 + x2 + x + 1

Построение декодированного конкретного циклического кода
Код, исправляющий одиночную ошибку. d₀ = 3.

1) Расчёт соотношении между контрольными и информационными символами кода.
n_k = log((n_u + 1) + log(n_u + 1))
2) Выбор образующего многочлена производится по таблице непреводимых двоичных многочленов. Образующий многочлен следует выбирать с минимальным числом элементов. Его степень должна быть больше или равна числу контрольных разрядов. Число элементов должно быть .
Пример: Построим циклический код d₀ = 3 для передачи шестнадцати сообщений.
n_u = 4 n_k = 3
k(x) = 1011 Строим единичную повёрнутую матрицу размером n_u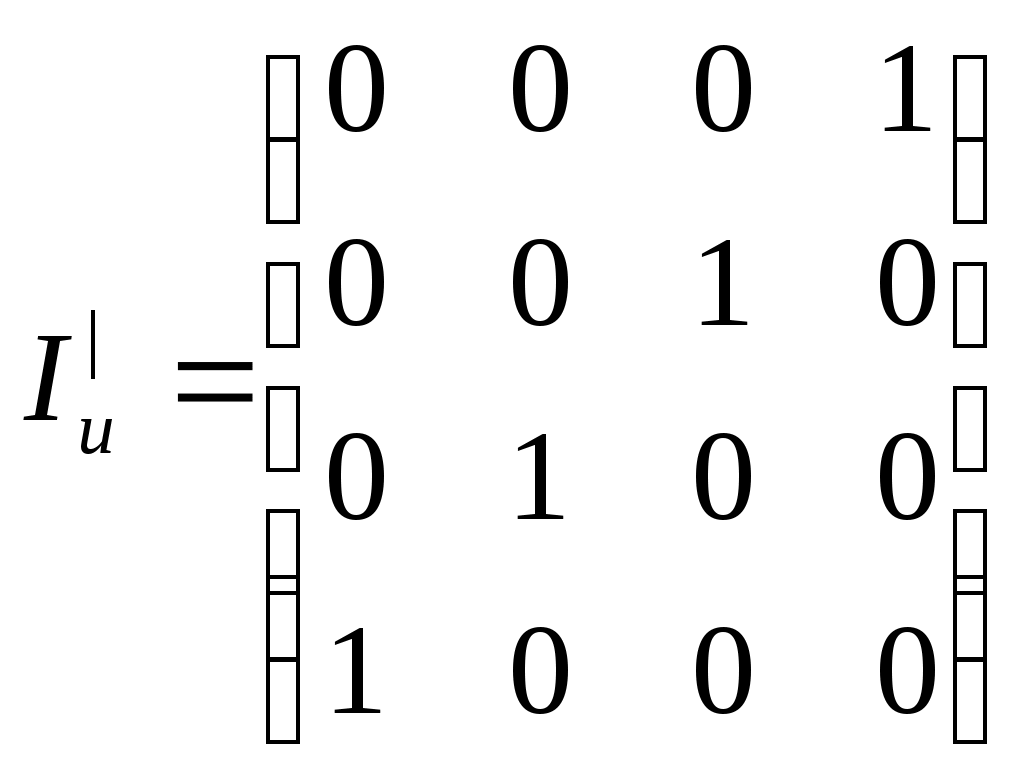

Находим остатки от делений последовательной строкина образующий многочлен.
1
Остаток

011

110

111

101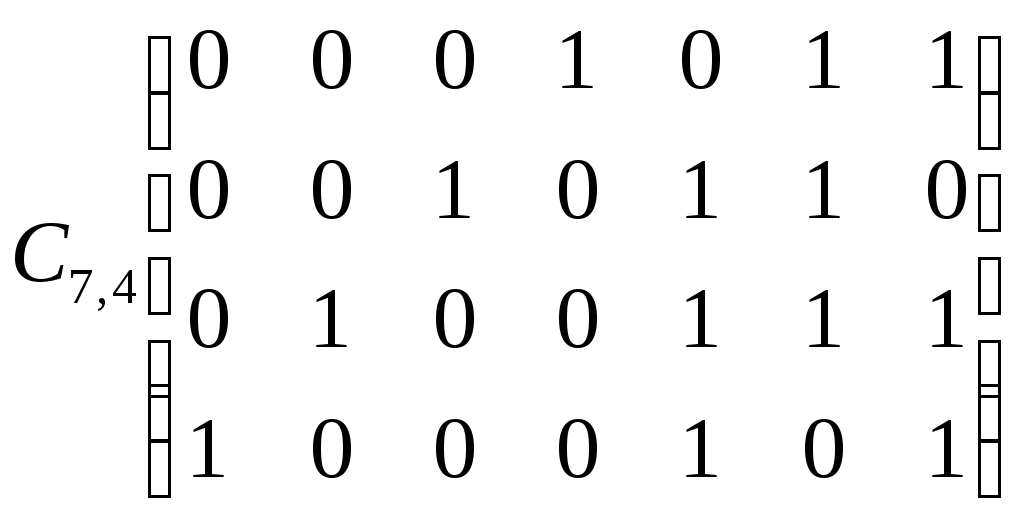


0000 1011

1011

01100

1011

1110

1011

101

1+2 2+4 1+2+3+4

1+3 3+4

1+4 1+2+3

2+3

Обнаружение и определение ошибок
Производится по остаткам деления принятого кодового вектора . Если в результате образовался остаток R(x) = 0, то комбинация принята без ошибок. Если есть остаток, то производят исправления. Для этого

1. 
   Определяют вес остатка
   

Если W_R S , где S – количество исправленных ошибок, то производят коррекцию. Для этого F(x) + R(x) и эта сумма даёт исправленную комбинацию.

Если вес W_R S , то производят циклический сдвиг F(x) влево, образуют новую комбинацию F₁(x).

Полученную комбинацию делят на обратный многочлен

- остаток

Если , то производят коррекцию F₁(x) + R₁(x), затем полученную комбинацию сдвигают вправо циклически на один разряд.
Если , то ещё раз сдвигаем циклически влево и т.д.
Пример: Пусть посылается комбинация u(x) = 0100111 (из обратной матрицы)

Пусть принята комбинация F(x) = 1100111, содержащая ошибку в единичном разряде

U(x) = 0100111 K(x) = 1011

F(x) = 1100111 S = 1

1 100111 1011

1 011

1111 R = 101

1011 W_R = 2 > S

1001

1011

101

1 001111 1011

1 011

1011 R₁ = 1

1011 = 1 = S  можем производить коррекцию

01
F₁(x) + R₁(x) 1001111

1

1001110
Циклически сдвигаем комбинацию вправо на один разряд 0100111 – исправляется кодовая комбинация.

Сложение двух соседних комбинаций циклического кода эквивалентно операции умножения первого слагаемого на x + 1.
000101 две комбинации из производящей матрицы

001010 (x² + 1) * (x +1) = x³ + x +x² +1 = 001111

001111
Образующие многочлены представляют собойьнеприводимые многочлены.
Коды, обнаруживающие трёхкратные ошибки
Методика построения следующая:

1) Выбор числа корректирующих разрядов

n_k – количество корректирующих разрядов



Значения логарифма округряется до целых чисел в большую сторону
Пример: n_u = 2 = 4

2) Выбор образующего многочлена. Он производится исходя из следующих соображений: для обнаружения трёхкратной ошибки надо иметь d₀ = r + 1 = 3 + 1 = 4 степень обратного многочлена должна быть больше или равна четырём, т.е.
Этот многочлен получают как произведение многочлена степени (n_k - 1)т.е. 3, который позволяет обнаруживать все двойственные ошибки и многочлены первой степени (x + 1), который обнаруживают любое количество нечётных ошибок. Полученный многочлен унаследует корректирующие свойства, т.е. он будет обнаруживать одиночную и тройную ошибки, используя корректирующие свойства многочлена x + 1 и будет обнаруживать двойные ошибки, используя свойства Шеннона, например x³ + x² +1.

Произведём умножение

M₁ = x + 1

M₃ = x³ + x² + 1

M₁ x M₃ = (x + 1)( x³ + x² + 1) = x⁴ + x² + x +1 = k(x)

x³ + x³ = 0 k(x) = 10111

x³ + x³ + x³ = x³
3) Построение образующей матрицы

П роизводят нахождением остатка последней строки единичной повёрнутой матрицы на обратный многочлен 100…к(х) - методика в прошлой лекции. Второй способ умножением строки единичной матрицы на образующий многочлен. Остальные комбинации получают суммированием комбинаций строк.
4) Обнаружение ошибок производят по остаткам от деления принятого кодового вектора на образующий многочлен. Если остатки есть, то принята ошибочная комбинация.

Пример: Строим код на четыре комбинации
01 х к(х) = 01 x 10111 = 010111

10 х к(х) = 10 х 10111 = 101110
Обратная матрица


Обнаружение ошибки

1) Тройная ошибка
v₁ = 010111

v _k = 111011 k_x = 10111

10111

10101 R_x = 10  обнаружена ошибка, надо повторить передачу

10111

0010
2) Двойная ошибка
v₁ = 010111

v
R_x = 1010 – есть остаток, следовательно, посланная комбинация содержит ошибку.
_k = 110011 k_x = 10111

10111

11101

10111

1010
3) Однократная ошибка
v₁ = 010111

v
R_x = 1110 – есть остаток, следовательно, принятая комбинаяция содержит ошибку. Какую ошибку мы не указываем.
_k = 110111 k_x = 10111

10111

11001

10111

1110
Пример: Построить образующий многочлен для создания циклического кода, обнаруживающего все трёхкратные ошибки при передаче 1000 сообщений.
1) Определение количества параметров кода
n_u = log₂ 1000 = 10

n_k 1 + log₂(n_u + 1 + log₂(n_u + 1)) = 1 + log₂(11 + log₂11)

n_k = 5

d₀ = r + 1 = 4 – число ненулевых членов образующего многочлена
Из таблицы нериводимых многочленов, выбираем многочлен степени n_{k – 1} = 4, который позволяет обнаруживать двойные ошибки.

M₄ = x⁴ + x + 1

M₁ = x + 1
k(x) = M₁ + M₄ = (x + 1)(x⁴ + x + 1) = x⁵ + x⁴ + x² + 1 110101

Линейно групповые коды (ЛГК)
Линейными называются коды, в которых проверочные и информационные символы связаны значениями с законами линейной комбинаторики. Т.е. с помощью определённой линейной комбинации можно построить кодовую комбинацию.

Свойства ЛГК:

1) Сумма (разность) кодовых векторов даёт вектор принадлежащий данному коду.

ЛГК относят к систематическим кодам. Минимальное кодовое расстояние равно минимальному весу ненулевых кодовых векторов. ЛГК обозначается (П, n_u) и задаются с помощью производящих матриц. Производящая матрица строится, как результат слияния информационной (И) и проверочной (П) матриц.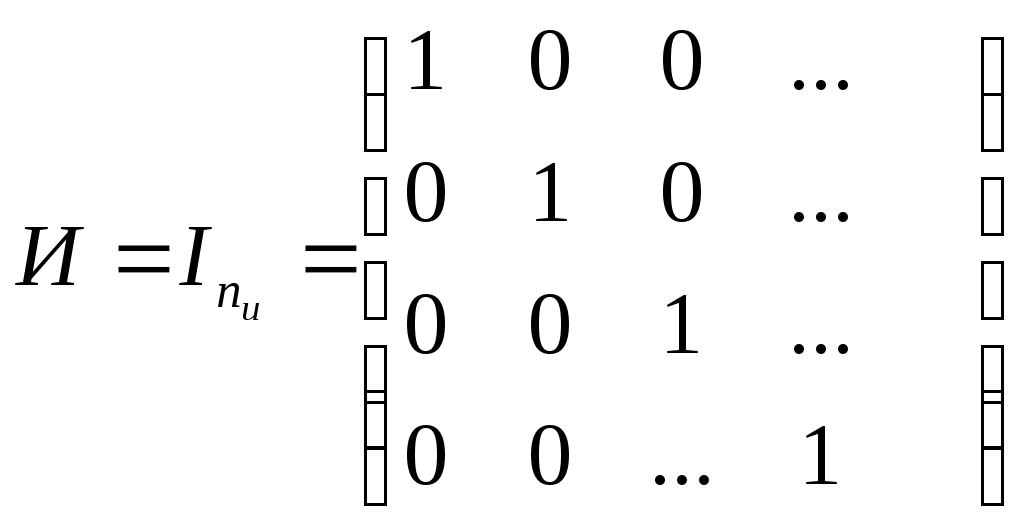



Матрица имеет n_k – столбцов и n_u – строк.

В качестве П выбирают комбинации один и ноль. При этом исходят из следующих соображений: чем больше единиц в матрице П, тем оптимальней считается матрица в точке обнаружения вероятности ошибок.

Вес каждой строки матрицы П W_П = d₀ – 1. Т.о. пораждающая матрица С приводится к следующему виду: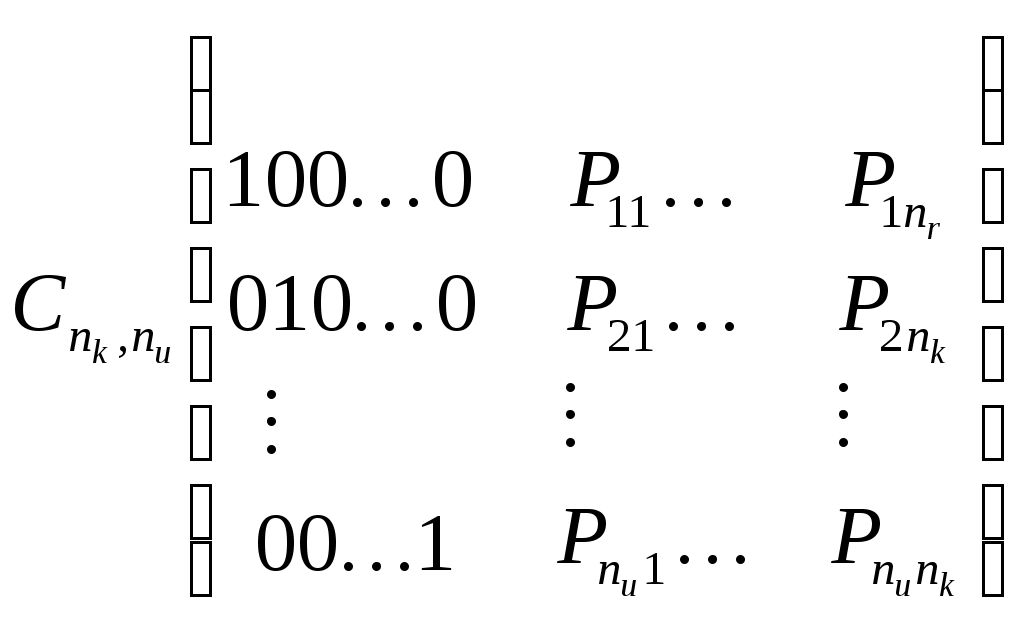



Строки производящей матрицы представляют собой n_u комбинации искомого кода. Остальные комбинации кода можно получить двумя способами:

1. 
   Их можно получить как результат сложения строк производящей матицы составленных в различных сочетаниях.
   
2. 
   ЛГК можно построить по производящей матрице, используя информационную часть кода, путём суммирования строк матрицы П.
   

П ример: Построить производящую матрицу для ЛГК, способную исправлять одиночную ошибку при передачи кода на 16 сообщений.

n_u = 4; n_k = log(n_u + 1 + log(n_u + 1)) = 3

d₀ = 3; n = 7 – значность кода

(единичная матрица)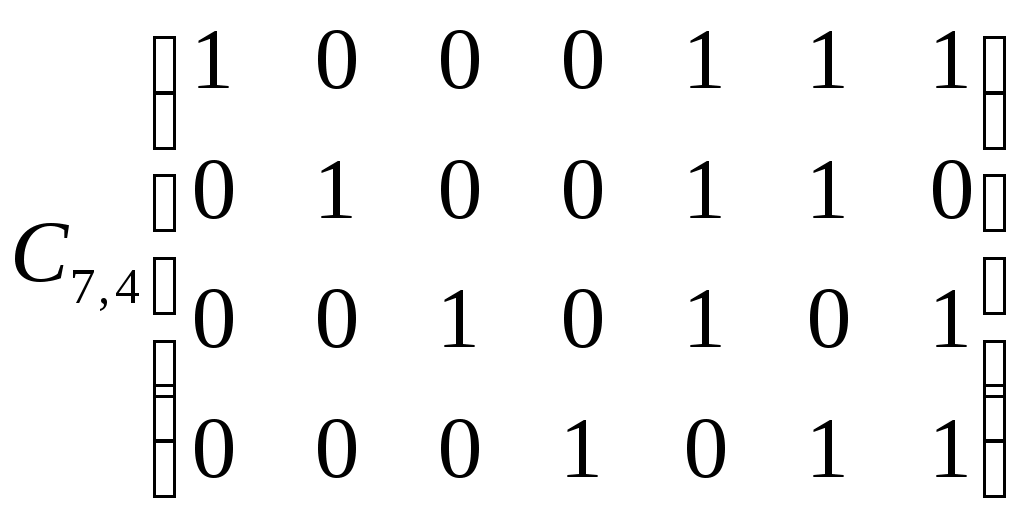


Пример: Построить образующую матрицу ЛГК, способную передавать 100 сообщений и исправлять одиночную ошибку.

N = 100 = ; n_u = 7; n_k = 4; n = 11;
Строим производящую матрицу: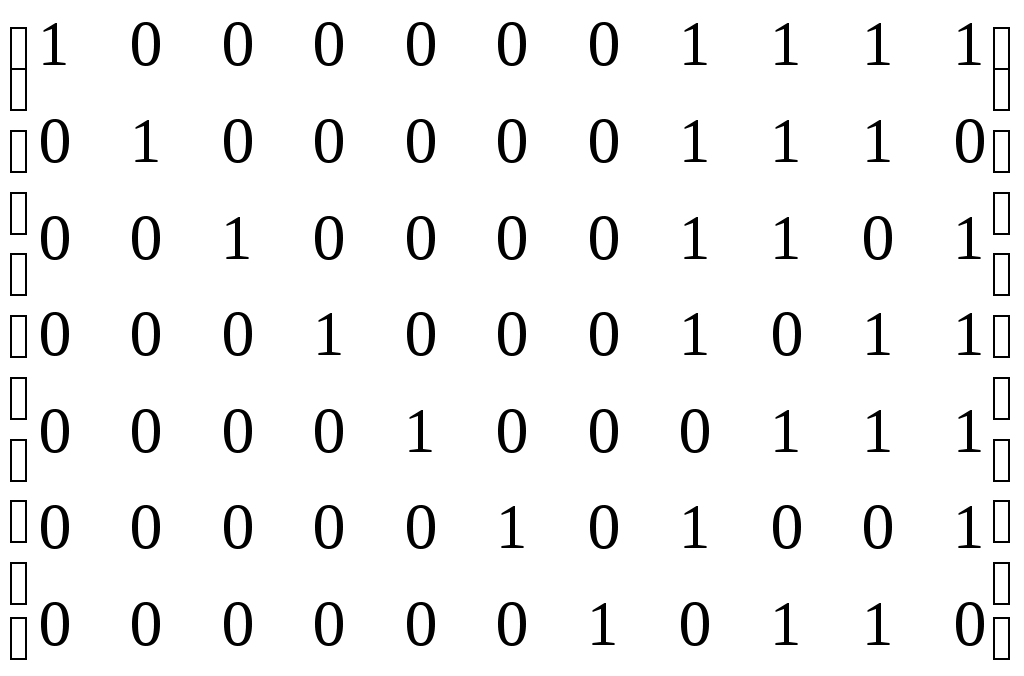





Пример: Построить групповой код по заданной производящей матрице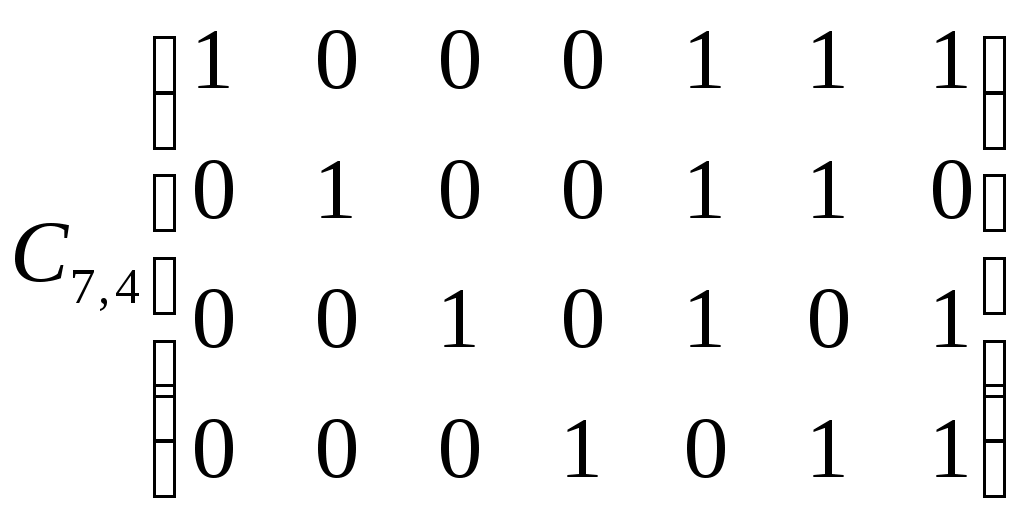


Выписываем информационные части кода:

1) 0000 5) 0010

2) 1000 6) 1010

3.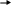 
   0 100 7) 0110 и т.д.
   
4. 
   1100 8) 1110
   

К каждой информационной части строим конкретный разряд:

1. 
   000
   
2. 
   111 – берём первую строку матрицы П
   
3. 
   110 – 2 – ю
   
4. 
   111 – складываем первую и вторую строку
   

110

001

5. 
   101
   
6. 
   111
   

101

010 - 1 - я + 3 - я

7. 
   110
   

101

011 - 2 - я + 3 - я

8. 
   111
   

110

001

100

Декодирование ЛГК

В процессе декодирования осуществляется проверки по определённой схеме. Число проверок равно числу контрольных разрядов. S(S₁, S₂, …, ) – строится проверочный вектор, который называется синдром. Если вес синдрома равен нулю, то комбинация принята правильно. Если какой – либо разряд содержит единицу, то имеется ошибка. Каждому разряду соответствует свой синдром. Вид синдрома определяется с помощью производящей матрицы. Набор синдромов содержится в специальной проверочной матрице H, которая строится из матрицы H = [П^ТI_nk] I_nk - единичная матрица. Столбцы матрицы представляют значение синдрома для каждого разряда.

Схема проверок: принятый сигнал v_x представляем в виде информационной части

v_x = (a₁, a₂, …,a_n, P₁, P₂,…,P_m)


Схема проверок строится:

1. 
   Проверка S₁
   

Суммируется разряд P₁ и те разряды из информационной части a₁ + …+ a_n, номера которых совпадают с номерами ненулевых разрядов первого столбца матрицы П.

2) Проверка S₂

Суммируется разряд P₂ и те разряды информационной части a₁ + …+ a_n, номера которых совпадают с номерами ненулевых разрядов второго столбца матрицы П.
Пример: Задана производящая матрица C_7,4 и составим схему проверок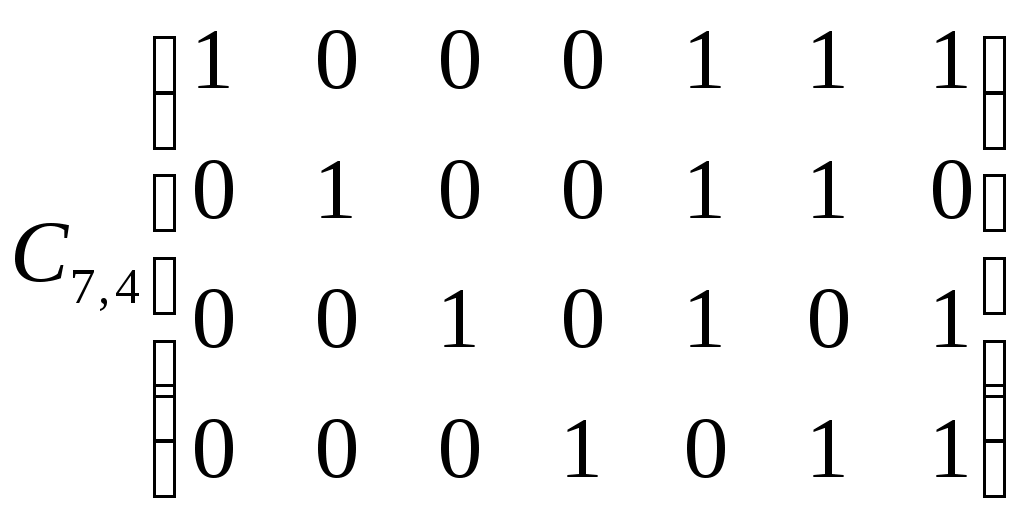


И П
S₁ = P₁ + a₂ + a₃ + a₄

S₂ = P₂ + a₁ + a₃ + a₄

S₃ = P₃ + a₁ + a₂ + a₃
Строим H: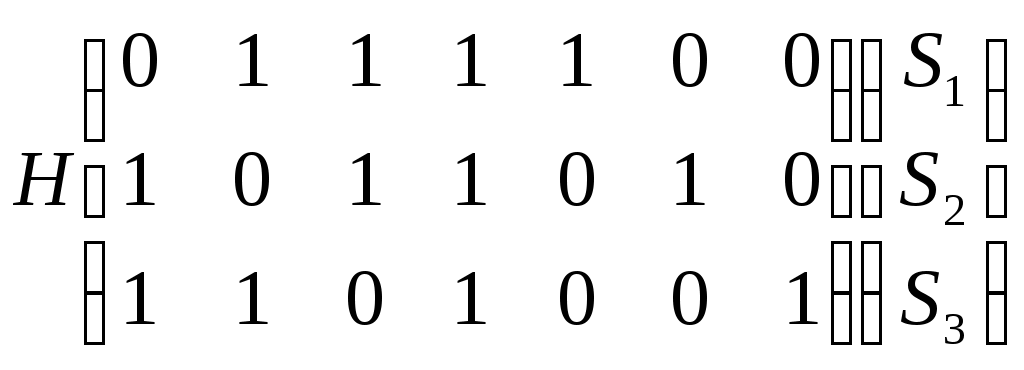



Если разряды синдрома соответствуют одному столбцу матрицы Н, т.е. S₁ = 0, S₂ = 1, S₃ = 1, то ошибка в первом разряде.
Пример: Пусть имеется информационная часть ЛГК, которая исправляет одиночную ошибку. Дана производящая матрица С_7,4. Получим корректирующие разряды, для этого сложим первую и вторую строку, следовательно, полный код.
a₁a₂ a₃a₄P₁P₂P₃

v₁ = 1100110 v_x = 1101110
Cхема проверок осталось такой же

Проведём проверки:

S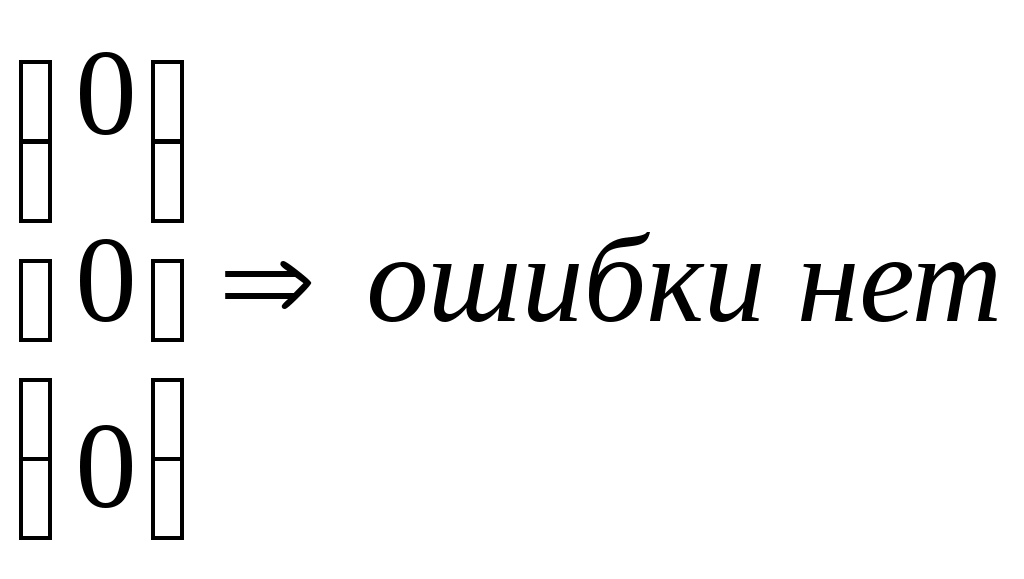

₁ = 1 + 1 + 0 + 0 = 0

S₂ = 1 + 1 + 0 + 0 = 0

S₃ = 0 + 1 + 1 + 0 = 0
П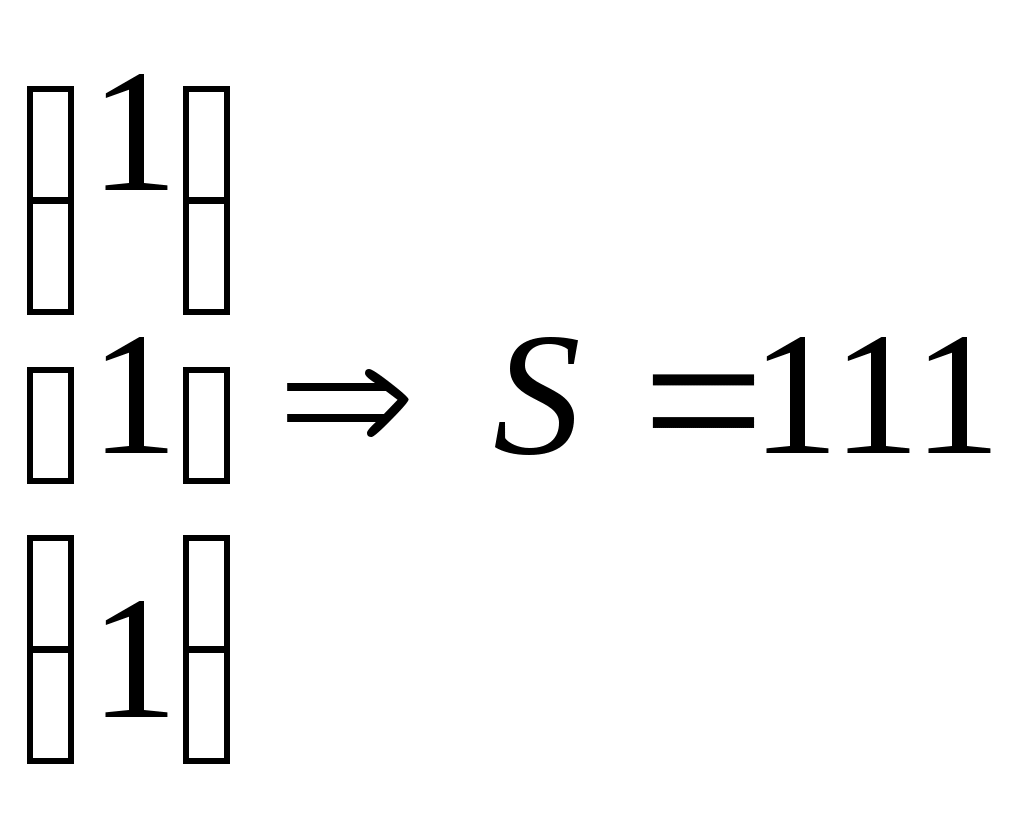

усть v_x = 1101110, т.е. ошибка в четвёртом разряде.
S₁ = 1 + 1 + 0 + 1 = 1

S₂ = 1 + 1 + 0 + 1 = 1 - это соответствует ошибке в четвёртому разряду

S₃ = 0 + 1 + 1 + 1 = 1

Информация. Язык. Общество 2

Измерение информации 2

Структурный метод 2

Статический метод 2

Энтропия и её свойства 3

Энтропия сложной системы 4

Условная энтропия. Объединение зависимых систем. 4

Полная условная энтропия 5

Определение информационных потерь в каналах связи 6

Энтропия и информация 8

Взаимная информация 9

Частная информация о системе 9

Количественное определения избыточности 12

Блочное кодирование 15

Передача информации по дискретным каналам связи 19

Код Хэминга 32

Декодирование кода Хэминга 33

Декодирование ЛГК 41