теория информации. ТИ (Best). Лекции по предмету "Теория информации" Красноярск 2002

• Название: Лекции по предмету "Теория информации" Красноярск 2002
• Анкор: теория информации
• Дата: 10.12.2022
• Размер: 1.06 Mb.
• Имя файла: ТИ (Best).doc
• Тип: Лекции; #837351
• страница: 9 из 12

Код Хафмана

Относят к группе неравномерных кодов. С помощью кодов Хафмана получают сообщения, в которых содержатся наименьшее среднее число символов на букву, т.е. это оптимизирующие коды.

Методика построения кодов следующая:

Пусть есть алфавит А, содержащий буквы а₁, а₂, …, а_n, вероятности появления которых р₁, р₂,…, р_n. Буквы алфавита располагаем в порядке убывания их вероятностей . Берем две последние буквы и объединяем их в одну букву b. Получаем новый алфавит А₁

а₁, а₂, …, а_n-2 b

p₁, р₂,…, р_n-2 p_n-1 + p_n
Алфавит А₁ называют сжатым, полученным из алфавита А путем однократного сжатия.

Буквы алфавита А₁ располагаем в порядке убывания их вероятностей. Затем проводим процедуру сжатия, получаем алфавит А₂. Продолжаем процедуру сжатия до тех пор, пока у нас не останется 2 буквы.

Буква а1 а2 а3 а4 а5 а6	А Вероятность 0,4 0 0,2 10 0,2 111 0,1 1101 0,05 11001 0,05 11000	Сжатые алфавиты
		А1 0,4 0 0,2 10 0,2 111 0,1 1101 0,1 1100	А2 0,4 0 0,2 10 0,2 111 0,2 110	А3 0,4 0 0,4 11 0,2 10	А4 0,6 (1) 0,4 (0)

Процедура кодирования
Две буквы последнего алфавита кодируем 1 и 0. Затем кодируется предыдущий алфавит. Процесс кодирования закончен. Чтобы определить эффективность, надо посчитать среднее число символов на алфавит.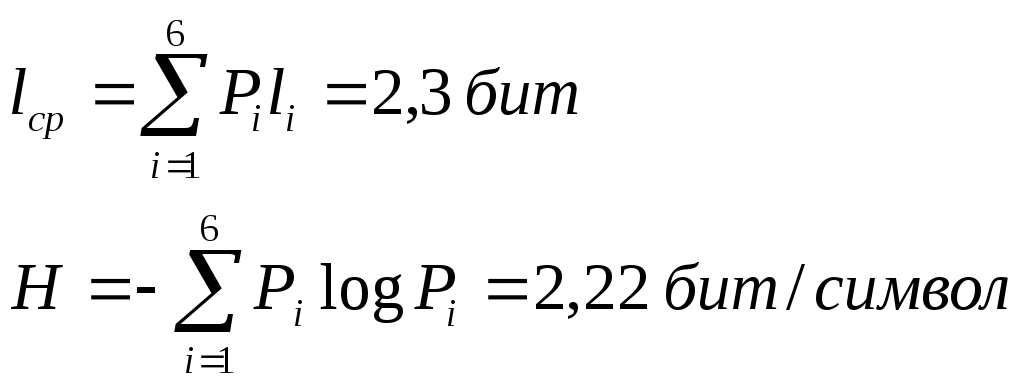



Кодирование алфавита по методу Хафмана не является однозначно определенной процедурой. Можно получать разные коды Хафмана.
Чтобы посмотреть изменение кода Хафмана, рассмотрим пример другой кодировки:

Буква а1 а2 а3 а4 а5 а6	А Вероятность 0,4 11 0,2 01 0,2 00 0,1 100 0,05 101 0,05 1010	Сжатые алфавиты
		А1 0,4 11 0,2 01 0,2 00 0,1 101 0,1 100	А2 0,4 11 0,2 10 0,2 01 0,2 00	А3 0,4 0 0,4 11 0,2 10	А4 0,6 (1) 0,4 (0)

Если посчитать , то оно не изменилось ,т.е. каким образом кодировать роли не играет.

Процедура декодирования кодов Хафмана является однозначной.

Используя методику Хафмана, можно строить оптимальные коды, если для кодирования используется m элементарных сигналов. При построении таких кодов используется процедура сжатия, при которой сливаются каждый раз m букв алфавита. Последовательность сжатия приводит к алфавиту из m букв.

Число букв исходного алфавита n должно быть представляемо n = m + k *(m -1), k – целое число. Этого условия всегда можно достичь, если ввести в исходный алфавит фиктивные буквы, вероятность которых равна нулю.

Дан алфавит из 6 букв с вероятностями. Построить троичный код Хафмана 0, 1, 2.
Требуемое число букв:

n = 3 + k * (3 - 1),

k = 1 n = 5

k = 2 n = 7

не хватает одной буквы а₇ с вероятностью равной нулю

Буква а1 а2 а3 а4 а5 а6 а7	А Вероятность 0 0,4 2 0,2 10 0,2 11 0,1 120 0,05 121 0,05 122 0	С ж а т и е
		А1 0 0,4 2 0,2 10 0,2 11 0,1 12 0,1	А2 0,4 (0) 0,4 (1) 0,2 (2)

Подсчитаем энтропию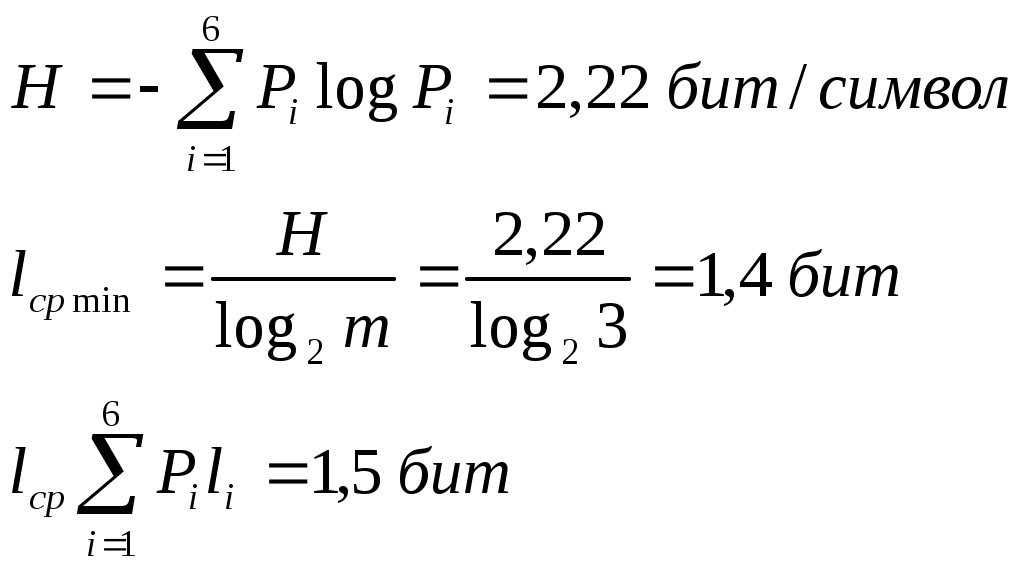

m – количество символов

Существует еще одна методика

С
1

0

1

(7)
хема получения кода Хафмана с помощью кодового дерева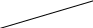




Д
1

0
ан алфавит. Располагаем буквы в порядке убывания вероятностей


1

0

(5)

0,5

(6)

1. 
   а
   0,28
   ₁ 0,5
   

0
0,22

0,08

0,05

(4)
01 а₂ 0,15

011 а₃ 0,12 1

0
(2)
10 а₄ 0,1 0

0
0,13
0011 а₅ 0,04 1

0
(3)
0010 а₆ 0,04 0

0
(1)
0001 а₇ 0,03 1

00000 а₈ 0,02 0

1. 
   Находят 2 буквы с вероятностями (а₇ и а₈) и проводят от них линию к точке, в которой вероятность равна их сумме
   
2. 
   Теперь меньшими вероятностями обладают буквы а₅ и а₆. Соединяют их линиями в одной точке с вероятностью 0.08
   
3. 
   Соединяем 0,08 и 0,05, получает 0,13
   
4. 
   Соединяем буквы а₃ и а₄
   
5. 
   Соединяем 0,15 и 0,13
   

И так далее…
Кодируем ветки

Обозначим цифрой один верхнюю линию узла, нижнюю ноль.

Коды представляют собой последовательность 0 и 1, которые встречаются по пути от точки с вероятностью единица, до кодируемой буквы.
Передача информации по дискретным каналам связи
Для анализа информационных возможностей канала связи используется обобщённая информационная модель каналов связи.





Z X Y И



ЛС
ИИ – источник информации

П₁, П₂ – преобразователи

ЛС – линия связи

ИП – источник помех

ПИ – приёмник информации

Источник информации создаёт cигналы z, которые кодируются в преобразователе П1, превращаются в сигналы x и поступают в линию связи (ЛС). В результате действия помех, сигнал Y на приёмном конце, отличается от X. Помехи создаются воображаемым источником помех (ИП) и поступают в линии связи в виде мешающего сигнала . Преобразователь П2 декодирует сигналы, и передаёт в приёмник информации. Приёмник информации перерабатывает принятое сообщение. Для организации эффективной передачи информации решают три задачи:

1. 
   Определение максимально возможной скорости передачи информации по каналу;
   
2. 
   Разработка кодов, позволяющих увеличить скорость передачи информации;
   
3. 
   Согласование канала с источником.
   

Важнейшей характеристикой канала является пропускная способность (обозначается символом С). - Наибольшая возможная скорость передачи информации по каналу. Пропускная способность определяют следующим образом:

, где V_x- средняя скорость передачи символов, I_yx – максимальное возможное значение среднего количества информации на один символ принятого сигнала.

, - средняя длительность передаваемых символов

Взаимная информация

- характеризует потери информации.
При отсутствии помех H(x / y) = 0 и . А максимальные I_yx = log₂m

Пропускная способность канала

m – количество символов алфавита, который кодируется
Основная теорема Шеннона о кодировании

для дискретного канала без помех
1). Дискретный канал без помех:

Основная теорема Шеннона утверждает: если источник информации имеет энтропию H(z), а канал связи обладает пропускной способностью, то:

1. Сообщения, вырабатываемое источником всегда можно закодировать так, чтобы скорость их передачи v_z была сколь угодно близка к v_{z max} .



2. Не существует способа кодирования, позволяющего сделать эту скорость больше, чем v_{z max.}

Величина - называется потоком информации, т.е. согласно Шеннона, при потоке информации существует способ кодирования, при котором можно вырабатывать всю информацию, переданную источником. Если то такого способа кодирования не существует.

Теорема Шеннона (другая). Если источник информации имеет энтропию Н(z), то сообщение всегда можно закодировать так, чтобы средняя длина кода l_ср была близка к величине



Доказательство: В качестве доказательства будем использовать методику Шеннона-Фана. Предположим, что при последовательном делении совокупности кодируемых букв по методу Шеннона-Фана на меньшие группы, каждый раз удается добиться равенства вероятностей двух получаемых групп.

1. После первого деления, получается группа с вероятностью ½;

2. После второго деления, получается группа с вероятностью ¼;

и т. д. ….

После -делений получим группы с вероятностью .

Если после -делений в группе будет одна буква, то она будет иметь -значное кодовое обозначение.

При выполнении этого условия длина кодового обозначения l_i будет связана с вероятностью p_i соотношением p_i=½l_i или, преобразуя это выражение, получим l_i = log = - log p_i.

В общем случае величина log p_i целым числом не будет, поэтому в качестве _i выбираю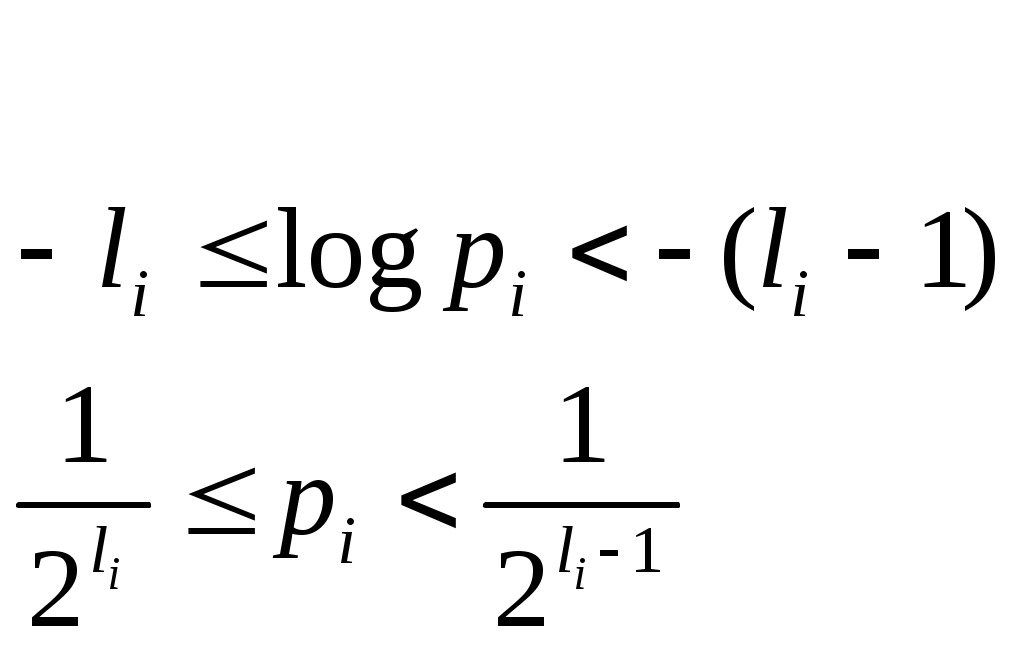т ближайшее большее целое число.

Величина _i будет лежать:



Далее Шеннон утверждал, что существует такой метод кодирования, при котором длина

_i = - log p_i

В качестве доказательства рассмотрим процедуру кодирования:

Пусть имеется алфавит с буквами и заданы вероятности их появления. Расположим буквы алфавита в порядке убывания их вероятностей.



к оды

z₁ Q₁ - числа Q_i будем определять следующим образом; Q₁ = 0

z₂ Q₂ Q₂=p(z₁)

_{… …} Q₃=p(z₁) + p(z₂)

z_n Q_n …

Q_n = p(z₁) + p(z₂) + … + p(z_n-1)
Все Q_i≠0, кроме первого, следовательно, совпадения с первым не будет, все Q_i – разные и меньше единицы. Шеннон предлагает перевести каждое Q_i число в двоичную дробь.

В целом .

Эти числа можно определить из соотношения:



q_i – либо 1, либо 0.

Пример: …

Разложение каждого числа ограничивается до тех пор, пока не будет выполняться равенство:


Пример: Дан алфавит состоит из восьми букв и их вероятности. Рассмотрим процедуру кодирования

Буква	Вероятность	- log pi	li	Qi	коды
z1	1/4	2	2	0	00
z2	1/4	2	2	1/4	01
z3	1/8	3	3	2/4	100
z4	1/8	3	3	5/8	101
z5	1/8	3	3	6/8	110
z6	1/16	4	4	7/8	1110
z7	1/32	5	5	15/16	11110
z8	1/32	5	5	31/32	11111

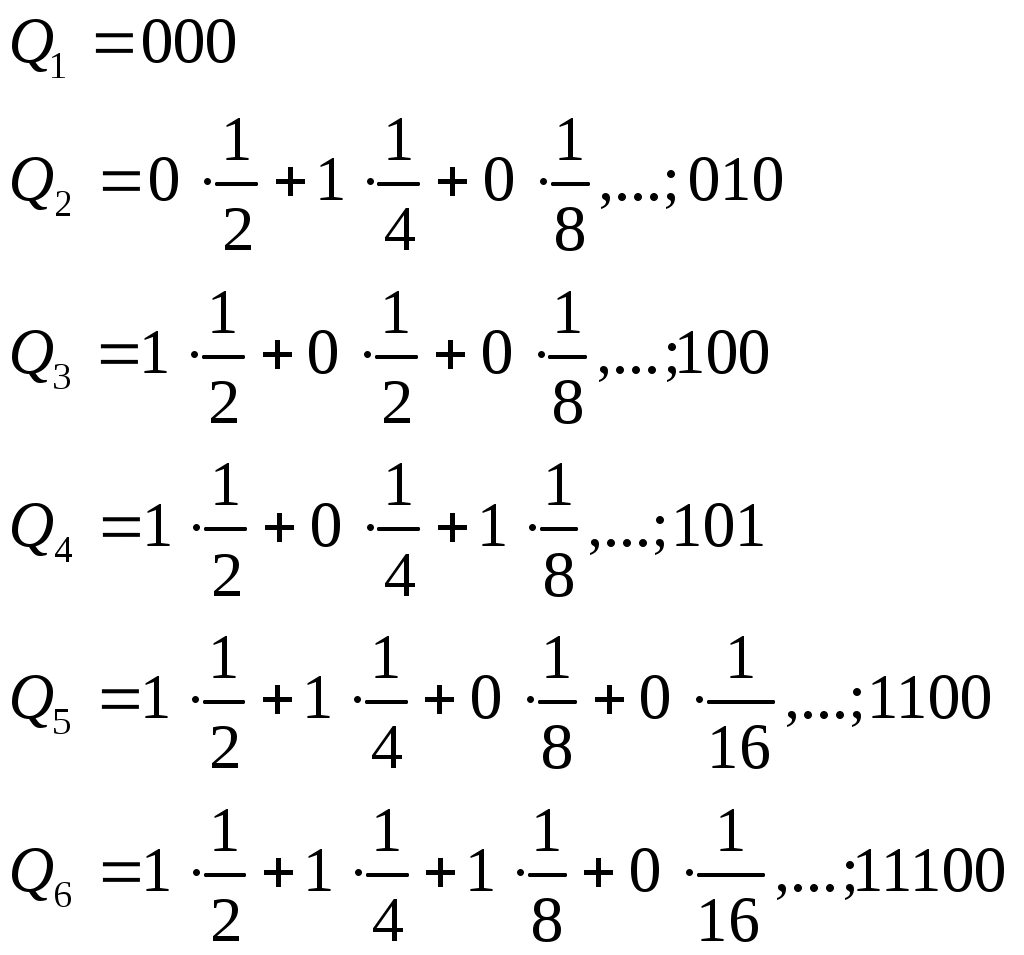Средняя длина кодового сообщения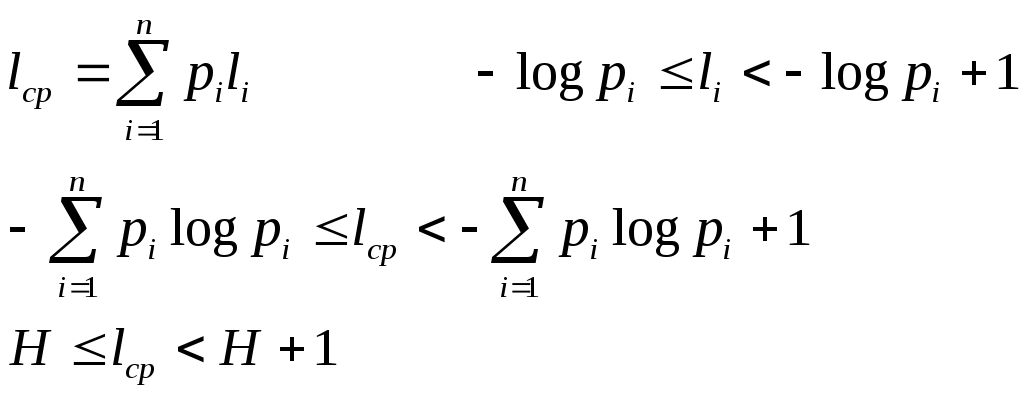



Теорема доказана
В случае кодирования буквенных блоков по N букв, получаем новый алфавит z’.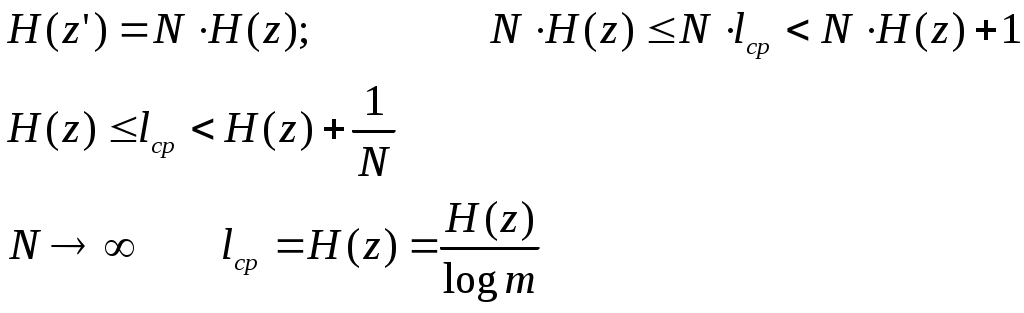

m – количество символов во вторичном алфавите, в двоичном - m = 2.

Скорость передачи Максимальная скорость