Ввод информации на рабочий лист. Лекция 1 интерфейс microsoft excel 4 лекция 2 работа с документом. Ввод и редактирование данных 6

• Название: Лекция 1 интерфейс microsoft excel 4 лекция 2 работа с документом. Ввод и редактирование данных 6
• Дата: 23.06.2022
• Размер: 4.72 Mb.
• Имя файла: Ввод информации на рабочий лист.doc
• Тип: Лекция; #611661
• страница: 4 из 6

ЛЕКЦИЯ 4: ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ. О ФИНАНСОВЫХ ФУНКЦИЯХ

Финансовые функции используют в планово-экономических расчетах. Всего в категории "Финансовые" имеется 53 функции.
Расчет амортизационных отчислений

Для расчета амортизационных отчислений необходимо знать, по крайней мере, три параметра:

1. 
   начальная стоимость имущества;
   
2. 
   остаточная стоимость по окончании эксплуатации;
   
3. 
   продолжительность эксплуатации.
   

Для расчета амортизационных отчислений могут быть использованы различные принципы и методики. В зависимости от этого могут быть применены и различные функции.
Линейный метод

В простейшем случае амортизация разносится равномерно на каждый год эксплуатации имущества. Для расчета величины амортизационных отчислений в этом случае используют функцию АПЛ.

Синтаксис функции:

АПЛ(А;В;С),

где A – начальная стоимость имущества;

В– остаточная стоимость имущества;

C – продолжительность эксплуатации.

Например, приобретено оборудование стоимостью 97000 руб. Продолжительность эксплуатации оборудования – 8 лет. Остаточная стоимость – 7500 руб. Величина амортизационных отчислений составит 11187,50 руб. за каждый и любой год эксплуатации (рис. 4.1).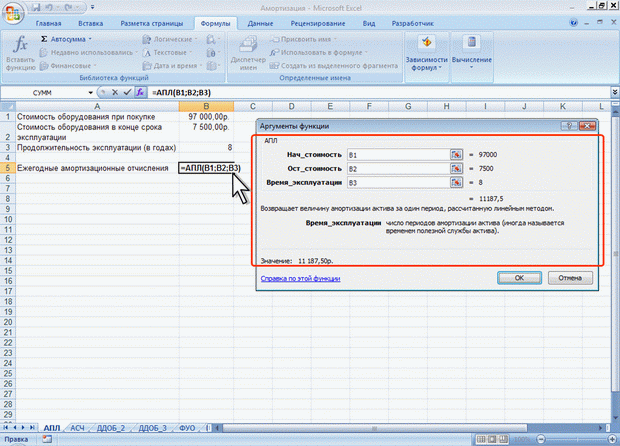



Рис. 4.1.  Расчет амортизационных отчислений линейным методом
Метод "суммы чисел"

В более сложном случае необходимо учитывать, что стоимость имущества в процессе его эксплуатации уменьшается. Следовательно, с каждым годом эксплуатации должны уменьшаться и амортизационные отчисления. Однако суммарно величина амортизационных отчислений должна составить разницу между начальной и остаточной стоимостью имущества. Для расчета величины амортизационных отчислений в этом случае используют функцию АСЧ.

Синтаксис функции:

АСЧ(А;В;С;D),

где A – начальная стоимость имущества;

В– остаточная стоимость имущества;

C – продолжительность эксплуатации;

D – год, для которого рассчитывается величина амортизационных отчислений.

Например, приобретено оборудование стоимостью 100000 руб. Продолжительность эксплуатации оборудования – 8 лет. Остаточная стоимость – 12000 руб. Величина амортизационных отчислений за первый год эксплуатации составит 19 555,56 руб., за второй год – 17 111,11 руб. и т. д. (рис. 4.2).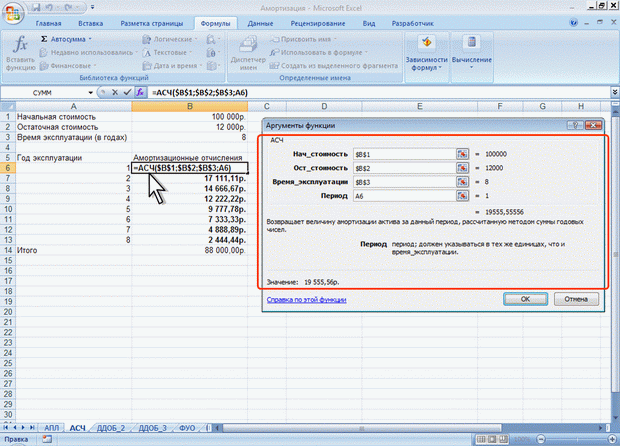



Рис. 4.2.  Расчет амортизационных отчислений методом "суммы чисел"
Метод двойного уменьшения остатка

Метод двойного уменьшения остатка вычисляет амортизацию, используя увеличенный коэффициент. Амортизация максимальна в первый период, в последующие периоды уменьшается. Для расчета величины амортизационных отчислений в этом случае используют функцию ДДОБ.

Синтаксис функции:

ДДОБ(А;В;С;D;Е),

где A – начальная стоимость имущества;

В– остаточная стоимость имущества;

C – продолжительность эксплуатации;

D – год, для которого рассчитывается величина амортизационных отчислений;

E – коэффициент, учитывающий процентную ставку снижающегося остатка. Если коэффициент опущен, то он полагается равным 2.

Например, приобретено оборудование стоимостью 100000 руб. Продолжительность эксплуатации оборудования – 8 лет. Остаточная стоимость – 12000 руб. Величина амортизационных отчислений за первый год эксплуатации составит 25000 руб., за второй год – 18 750,00 руб. и т. д. (рис. 4.3, рис. 4.1).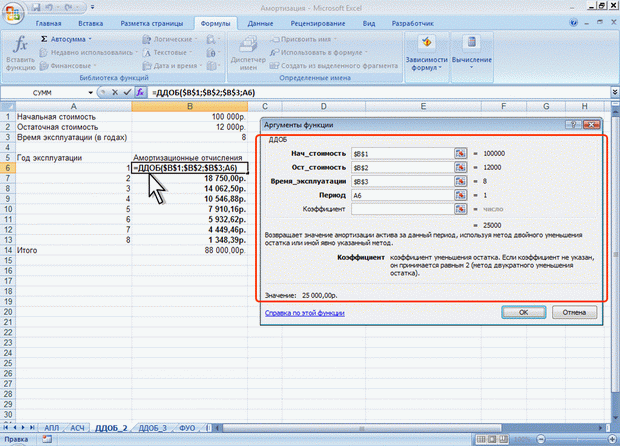



Рис. 4.3.  Расчет амортизационных отчислений методом двойного уменьшения остатка

При другом значении коэффициента уменьшения остатка, получатся другие значения амортизационных отчислений. Например, при уменьшении остатка в три раза, величина амортизационных отчислений за первый год эксплуатации составит 37500 руб., за второй год – 23 437,50 руб. и т. д. (рис. 4.4, рис. 4.1).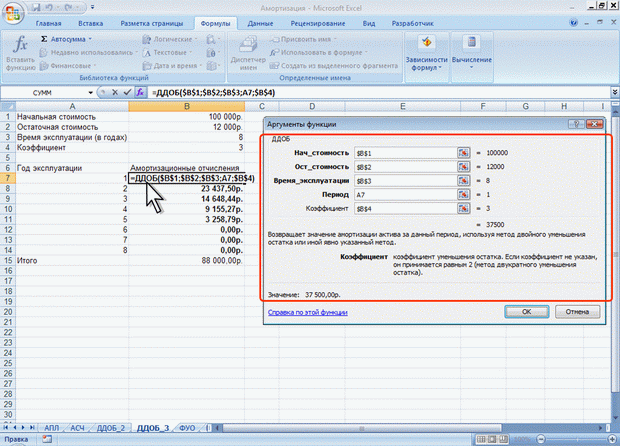



Рис. 4.4.  Расчет амортизационных отчислений методом тройного уменьшения остатка
Метод фиксированного уменьшения остатка

В тех случаях, когда имущество приобретается в середине года и необходимо рассчитывать амортизацию за несколько месяцев первого календарного года эксплуатации, а также за несколько месяцев последнего календарного года эксплуатации, следует применять функцию ФУО.

Синтаксис функции

ФУО(А;В;С;D;Е),

где A – начальная стоимость имущества;

В– остаточная стоимость имущества;

C – продолжительность эксплуатации;

D – год, для которого рассчитывается величина амортизационных отчислений;

E – месяцы первого календарного года эксплуатации.

Например, приобретено оборудование стоимостью 100000 руб. Продолжительность эксплуатации оборудования – 8 лет. Остаточная стоимость – 12000 руб. Величина амортизационных отчислений за три месяца первого календарного года эксплуатации составит 5 825,00 руб., за второй год – 21 942,78 руб. и т. д. За девять месяцев последнего (девятого) года эксплуатации – 2 569,92 руб. (рис. 4.5).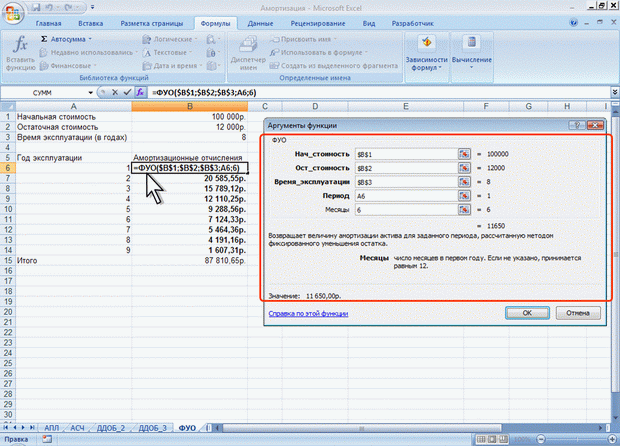



Рис. 4.5.  Расчет амортизационных отчислений методом фиксированного уменьшения остатка

К сожалению, часто эта функция дает некоторую погрешность в вычислениях.
Расчет амортизации для любого выбранного периода

При необходимости расчета амортизационных отчислений за любой произвольный период эксплуатации имущества следует использовать функцию ПУО.

Синтаксис функции

ПУО(А;В;С;D;Е;F;G),

где A – начальная стоимость имущества;

В– остаточная стоимость имущества;

C – продолжительность эксплуатации;

D – начальный период, для которого рассчитывается величина амортизационных отчислений;

E – конечный период, для которого рассчитывается величина амортизационных отчислений;

F – коэффициент, учитывающий процентную ставку снижающегося остатка. Если коэффициент опущен, то он полагается равным 2;

G – логическое значение, определяющее, следует ли использовать линейную амортизацию в том случае, когда амортизация превышает величину, рассчитанную методом снижающегося остатка. Если аргумент G имеет значение ЛОЖЬ или опущен, используется метод начисления линейной амортизации, если амортизация больше величины, рассчитанной методом снижающегося остатка. Если аргумент G имеет значение ИСТИНА, метод начисления линейной амортизации не используется, даже если амортизация больше величины, вычисленной методом снижающегося остатка.

Например, приобретено оборудование стоимостью 100000 руб. Продолжительность эксплуатации оборудования – 8 лет. Остаточная стоимость – 12000 руб. Величина амортизационных отчислений со второго по пятый годы эксплуатации включительно составит 32 519,53 руб. (рис. 4.6).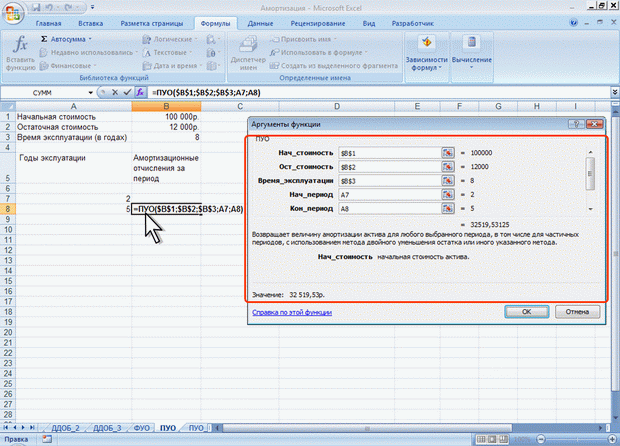



Рис. 4.6.  Расчет амортизации для любого выбранного периода (двойное уменьшение остатка)
Анализ инвестиций

Использование сложных процентов необходимо при вычислении доходности вкладов (инвестиций), сумм платежей по кредитам, сумм страховых платежей и т. п.

Во всех этих случаях для расчета необходимо знать, по крайней мере, три параметра:

1. 
   процентная ставка за период;
   
2. 
   общее число периодов платежей;
   
3. 
   выплата, производимая в каждый период или общая сумма.
   

Расчет суммы вклада (величины займа)

В зависимости от порядка расчетов могут быть различные функции. В простейших случаях для расчета можно использовать функцию БС. Эта функция вычисляет для будущего момента времени величину вложения, которое образуется в результате единовременного вложения и/или регулярных периодических вложений под определенный процент. Эту же функцию можно использовать для вычисления возможной величины займа под определенный процент, при определенных регулярных периодических выплатах по погашению займа.

Синтаксис функции

БС(А;В;С;D;Е),

где A – процентная ставка за период;

В– общее число платежей;

C – выплата, производимая в каждый период и не меняющаяся за все время выплаты;

D – требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, он полагается равным 0 (будущая стоимость займа, например, равна 0);

E – число 0 или 1, обозначающее, когда должна производиться выплата. 0 или опущен – в конце периода, 1 – в начале периода.

При создании формулы следует устанавливать одинаковую размерность периода для процентной ставки и числа платежей. Например, если платежи производятся один раз в год, то и процентная ставка должна быть дана в годовом исчислении, а если платежи производятся ежемесячно, то должна быть задана месячная процентная ставка.

Все аргументы, означающие денежные средства, которые должны быть выплачены (например, сберегательные вклады), представляются отрицательными числами; денежные средства, которые должны быть получены (например, дивиденды), представляются положительными числами.

При создании формулы не обязательно указывать все аргументы функции. Вместо отсутствующего аргумента в строке формул должна быть точка с запятой.
Например, необходимо рассчитать будущую сумму вклада в сумме 1000 руб., внесенного на 10 лет с ежегодным начислением 10% (рис. 4.7). Или будущую сумму вклада при тех же условиях, но с ежегодным внесением 1000 руб. (рис. 4.8).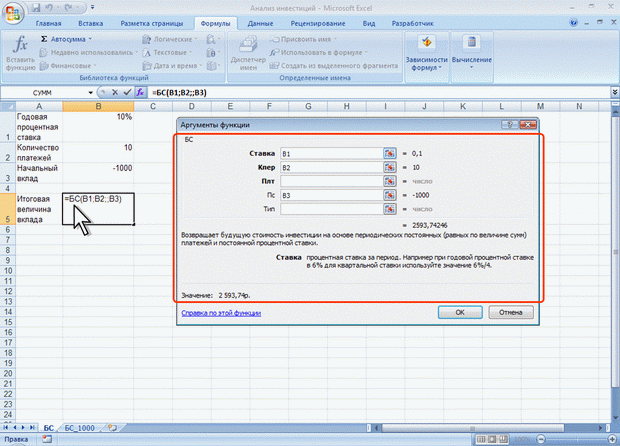



Рис. 4.7.  Расчет величины вклада с начальным взносом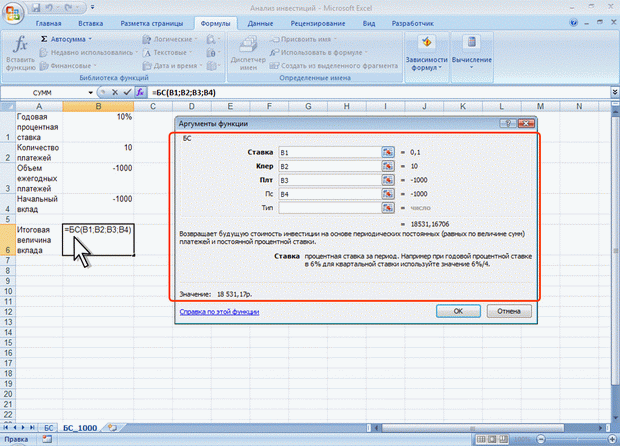



Рис. 4.8.  Расчет величины вклада с начальным взносом при регулярном пополнении

Результат вычисления: в первом случае - 2593,74 руб., во втором - 18531,17руб.
Или, необходимо рассчитать будущую сумму вклада при ежемесячном внесении 200 руб. в течение 8 лет с ежегодным начислением 6%. Начальный вклад равен 0 (рис. 4.9).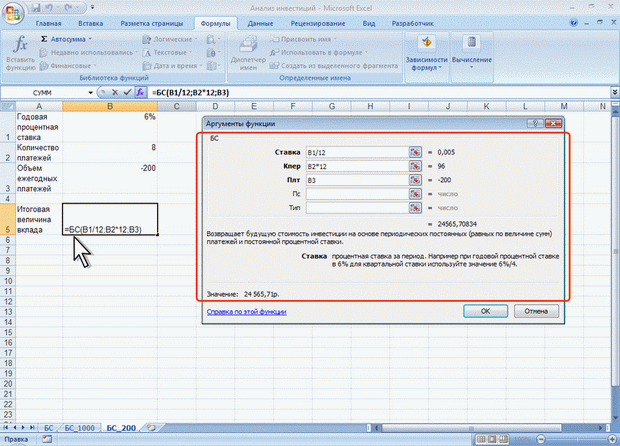



Рис. 4.9.  Расчет величины вклада без начального взноса при регулярном пополнении

Результат вычисления – 24 565, 71 руб.

Эту же формулу (см. рис. 4.9) можно использовать и для расчета величины возможного займа. Например, требуется рассчитать, какую сумму можно занять на 8 лет под 6% годовых, если есть возможность выплачивать ежемесячно по 200 руб. Результат будет тот же самый – 24 565,71 руб.

Расчет стоимости инвестиции

В зависимости от порядка расчетов могут быть различные функции. В простейших случаях для расчета можно использовать функцию ПС. Эта функция вычисляет для текущего момента времени необходимую величину вложения под определенный процент для того чтобы в будущем единовременного получить и/или периодически получать заданную сумму (доход).

Синтаксис функции

ПС(А;В;С;D;Е),

где A – процентная ставка за период.

В– общее число платежей.

C – выплата, производимая в каждый период и не меняющаяся за все время выплаты.

D – значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, он полагается равным 0.

E – число 0 или 1, обозначающее, когда должна производиться выплата. 0 или опущен – в конце периода, 1 – в начале периода.

При создании формулы следует устанавливать одинаковую размерность периода для процентной ставки и числа платежей. Например, если выплаты производятся один раз в год, то и процентная ставка должна быть дана в годовом исчислении, а если выплаты производятся ежемесячно, то должна быть задана месячная процентная ставка.

При создании формулы не обязательно указывать все аргументы функции. Вместо отсутствующего аргумента в строке формул должна быть точка с запятой.
Например, необходимо рассчитать величину вложения под 10 % годовых, которое будет ежегодно в течение 10 лет приносить доход 1000 руб. (рис. 4.10).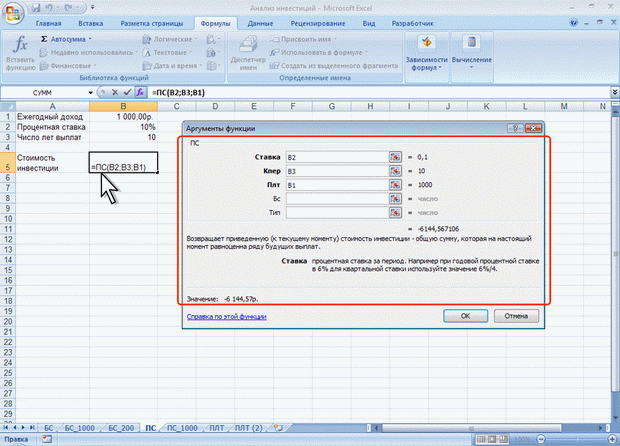



Рис. 4.10.  Расчет стоимости инвестиции

Результат вычисления получается отрицательным (-6 144,57 руб.) поскольку эту сумму необходимо заплатить.

Или, например, необходимо рассчитать величину вложения под 10 % годовых, которое через 10 лет принесет доход 10000 руб. (рис. 4.11).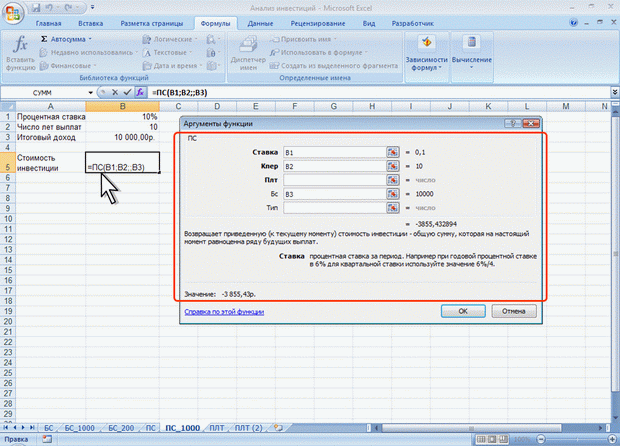



Рис. 4.11.  Расчет стоимости инвестиции

Результат вычисления получается отрицательным (-3855,43 руб.) поскольку эту сумму необходимо заплатить.
Расчет процентных платежей

В зависимости от порядка расчетов могут быть различные функции. В простейших случаях для расчета можно использовать функцию ПЛТ. Функция ПЛТ вычисляет размер периодических выплат, необходимых для погашения займа, полученного под определенный процент, за определенный срок. Эту же функцию можно использовать для вычисления величины регулярных вложений под определенный процент, необходимых для достижения определенной величины вклада за определенный срок.

Синтаксис функции

ПЛТ(А;В;С;D;Е),

где A – процентная ставка за период;

В– общее число платежей;

C – выплата, производимая в каждый период и не меняющаяся за все время выплаты;

D – требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, он полагается равным 0 (будущая стоимость займа, например, равна 0);

E – число 0 или 1, обозначающее, когда должна производиться выплата. 0 или опущен – в конце периода. 1 – в начале периода.

При создании формулы следует устанавливать одинаковую размерность периода для процентной ставки и числа платежей. Например, если выплаты производятся один раз в год, то и процентная ставка должна быть дана в годовом исчислении, а если выплаты производятся ежемесячно, то должна быть задана месячная процентная ставка.

При создании формулы не обязательно указывать все аргументы функции. Вместо отсутствующего аргумента в строке формул должна быть точка с запятой.
Например, необходимо рассчитать величину ежемесячного вложения под 6 % годовых, которое через 12 лет составит сумму вклада 50000 руб. (рис. 4.12).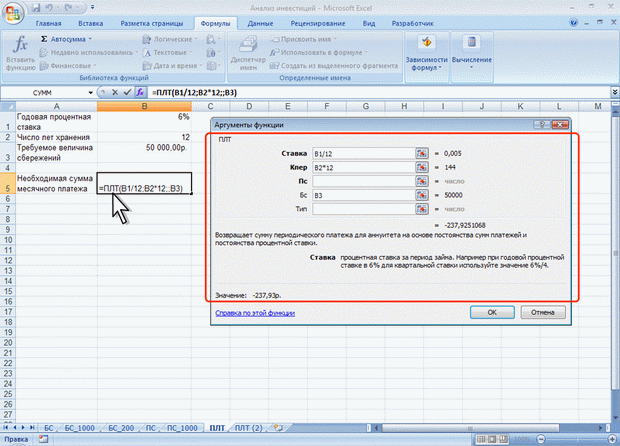



Рис. 4.12.  Расчет процентных платежей

Результат вычисления получается отрицательным (-237,95 руб.), поскольку эту сумму необходимо выплачивать.

Или при тех же условиях, но с начальным вкладом 10000 руб. (рис. 4.13).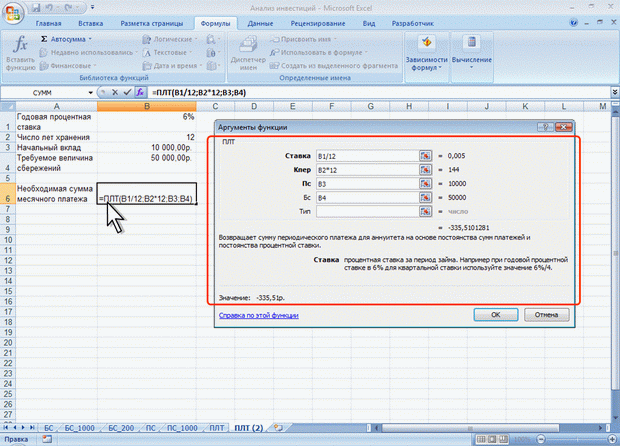



Рис. 4.13.  Расчет процентных платежей

Результат вычисления получается отрицательным (-335,51 руб.), поскольку эту сумму необходимо выплачивать.

Эту же формулу (рис. 4.12) можно использовать и при расчете платежей по займу. Например, необходимо рассчитать величину ежемесячной выплаты по займу в 50000 руб. под 6 % годовых на 12 лет. Результат будет тот же самый -237,95 руб.
Расчет продолжительности платежей

В зависимости от порядка расчетов могут быть различные функции. В простейших случаях для расчета можно использовать функцию КПЕР. Функция КПЕР вычисляет количество периодических выплат, необходимых для погашения займа, полученного под определенный процент. Эту же функцию можно использовать для вычисления количества периодических вкладов под определенный процент, необходимых для достижения определенной величины вклада.

Синтаксис функции

КПЕР(А;В;С;D;Е),

где A – процентная ставка за период;

В– выплата, производимая в каждый период и не меняющаяся за все время выплаты;

C – приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей;

D – требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, он полагается равным 0 (будущая стоимость займа, например, равна 0);

E – число 0 или 1, обозначающее, когда должна производиться выплата. 0 или опущен – в конце периода, 1 – в начале периода.

При создании формулы не обязательно указывать все аргументы функции. Вместо отсутствующего аргумента в строке формул должна быть точка с запятой.

Например, необходимо рассчитать количество ежемесячных платежей для погашения займа в 10000 руб., полученного под 10 % годовых, при условии ежемесячной выплаты 200 руб. (рис. 4.14).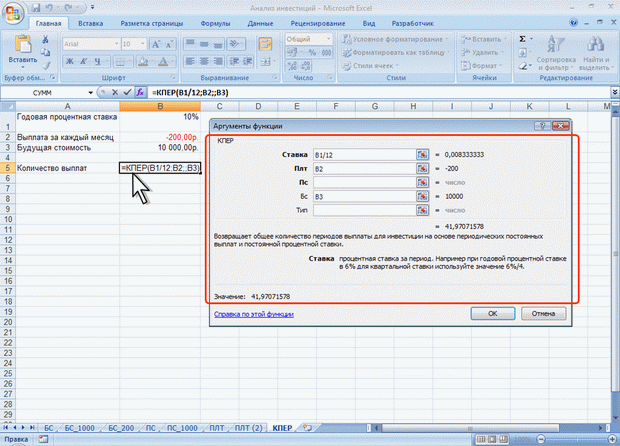



Рис. 4.14.  Расчет количества платежей с использованием функции КПЕР

Результат вычисления – 42 ежемесячные выплаты.
Использование логических функций. О логических функциях.

Логические функции используют для проверки и анализа данных, а также в условных вычислениях.

Вместо функций ЛОЖЬ и ИСТИНА можно непосредственно ввести слово с клавиатуры в ячейку или в формулу.

Логические функции в качестве аргументов используют логические выражения. Логические выражения используются для записи условий, в которых сравниваются числовые или текстовые значения. В логических выражениях используют операторы сравнения, приведенные в таблице.

Оператор	Значение
=	Равно
<	Меньше
>	Больше
<=	Меньше или равно
>=	Больше или равно
<>	Не равно

Проверка и анализ данных

Для наглядного представления результатов анализа данных можно использовать функцию ЕСЛИ.

Синтаксис функции:

ЕСЛИ(А;В;С),

где A – логическое выражение, правильность которого следует проверить;

В– значение, если логическое выражение истинно;

C – значение, если логическое выражение ложно.

Например, в таблице на рис. 4.22 функция ЕСЛИ используется для проверки значений в ячейках В2:В12 по условию <0,6%. Если значение удовлетворяет условию, то функция принимает значение "ДА", а если значение не удовлетворяет условию, то функция принимает значение "нет".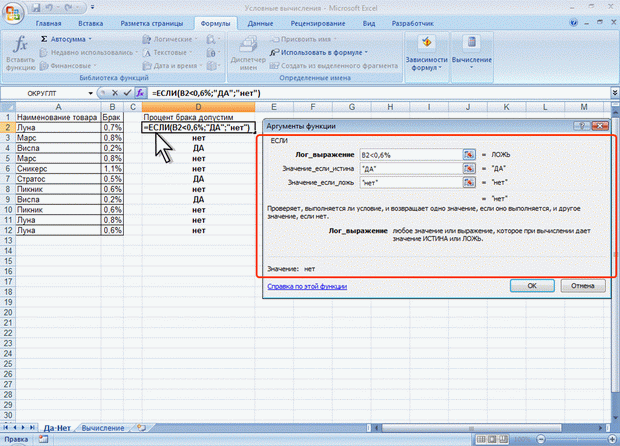



Рис. 4.22.  Проверка значений


Условные вычисления

Часто выбор формулы для вычислений зависит от каких-либо условий. Например, при расчете торговой скидки могут использоваться различные формулы в зависимости от размера покупки.

Для выполнения таких вычислений используется функция ЕСЛИ, в которой в качестве аргументов значений вставляются соответствующие формулы.

Например, в таблице на рис. 4.23 при расчете стоимости товара цена зависит от объема партии товара. При объеме партии более 30 цена понижается на 10%. Следовательно, при выполнении условия используется формула B:B*C:C*0,9, а при невыполнении условия – B:B*C:C.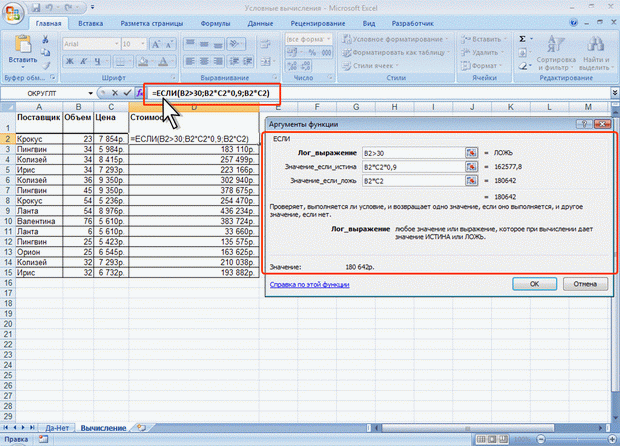



Рис. 4.23.  Условное вычисление