физика. KVANTOVAYa_OPTIKA (копия). Лекция 1 Тепловое излучение. Законы теплового излучения. Фотонный газ. Давление света
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
|
За преградой поставили фотопластинку. Сначала пропустили пучок через одну щель, потом через другую. На пластинке возникли почернения в виде кривых 1 и 2. Затем открыли обе щели и пропустили пучок через них. Оказалась, что возникшая картина не является наложением двух предыдущих, это свидетельствует о влиянии обоих отверстий на движение каждого электрона. Такой вывод не совместим с представлением о траекториях. Если бы электрон находился в каждый момент времени в определенной точке пространства, то он проходил бы только через одно отверстие. Явление же дифракции доказывает, что в прохождении каждого электрона участвуют оба отверстия. Однако это не означает, что через каждое отверстие проходит часть электрона, так как электрон, как и любая микрочастица, является неделимым целым. Проведенный эксперимент доказывает, что микрочастицы обладают свойствами особого рода, совершенно отличными от свойств макрочастиц. Из сказанного следует, что монохроматический поток микрочастиц при определенных условиях будет вести себя как плоская монохроматическая волна с волновым числом 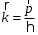 и частотой и частотой 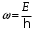 . Эту волну называют волной де Бройля или волной материи и её можно описать комплексной функцией вида: . Эту волну называют волной де Бройля или волной материи и её можно описать комплексной функцией вида: 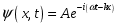 или или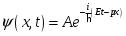 , где i- мнимая единица. , где i- мнимая единица.Следует отметить, что волна де Бройля, так же как и любая волна в процессе распространения может отражаться, преломляться, интерферировать и дифрагировать по обычным волновым законам. Фазовая скорость этой волны 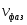 , т.е. скорость, с которой распространяется в пространстве точка волны с постоянной фазой, определяется соотношением: , т.е. скорость, с которой распространяется в пространстве точка волны с постоянной фазой, определяется соотношением: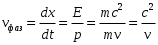 . .Полученное соотношение показывает, что 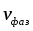 может быть больше скорости света в вакууме. Однако это не противоречит теории относительности, которая запрещает движение со скоростью большей скорости света в вакууме лишь для процессов, связанных с переносом энергии или массы. Фазовая скорость не характеризует ни один из этих процессов. может быть больше скорости света в вакууме. Однако это не противоречит теории относительности, которая запрещает движение со скоростью большей скорости света в вакууме лишь для процессов, связанных с переносом энергии или массы. Фазовая скорость не характеризует ни один из этих процессов. Групповая скорость волны де Бройля 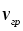 равна скорости движения частицы в пространстве. равна скорости движения частицы в пространстве.В случае нерелятивистской частицы, когда массу частицы можно считать равной её массе покоя 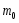 , длина волны материи связана с энергий частицы соотношением: , длина волны материи связана с энергий частицы соотношением: 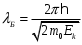 . .В случае релятивистской частицы 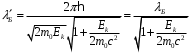 . .В случае нерелятивистского электрона соответствующая длина волны де Бройля будет равна 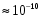 м. м. Соотношение неопределенностей Гайзенберга. Соотношение неопределенностей Гайзенберга.В классической механике состояние макрочастицы определяются заданием значений координат, импульса, энергии и т.д. Эти величины называются динамическими переменными. Как уже говорилось, своеобразие свойств микрочастицы проявляются в том, что для определения её состояния не для всех переменных, которые должны определять это состояние, могут быть получены конкретные значения. В 1927 году немецкий физик Гайзенберг математически доказал, что: произведение неопределенностей значений двух канонически сопряженных переменных не может быть по порядку величины меньше постоянной Планка. Это утверждение называется принципом неопределенности Гайзенберга. В механике канонически сопряженными являются пары переменных: координата (x,y,z) и импульс ( 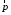 ); энергия Е и время t. ); энергия Е и время t.Математически принцип неопределенности можно записать: 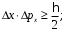 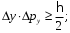 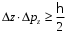 или 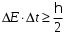 . .Рассмотрим микрочастицу свободно летящую вдоль оси ОY. Поставим на ее пути преграду со щелью шириной 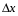 , расположенную перпендикулярно направлению ее движения, , расположенную перпендикулярно направлению ее движения,
|