Лекции по схемотехнике ЭВМ. Лекция Базовые понятия цифровой электроники версия для печати и pda в лекции рассказывается о базовых терминах цифровой электроники, о цифровых сигналах, об уровнях представления цифровых устройств, об их электрических и временных параметрах
 Скачать 5.63 Mb. Скачать 5.63 Mb.
|
|
Все регистры, имеющие выход с тремя состояниями, обеспечивают повышенную нагрузочную способность. Задержка переключения регистров примерно соответствует задержке переключения триггеров. Все временные ограничения, накладываемые на входные сигналы в случае триггеров, справедливы и для входных сигналов регистров. Например, не должна быть слишком малой длительность сигнала С, а также не должна быть слишком малой задержка между установлением сигнала D и приходом положительного фронта сигнала С. Иначе работа регистра может быть нестабильной или даже неправильной. Одно из основных применений регистров состоит в хранении требуемого кода в течение нужного времени. Если для работы остальной части схемы необходимо иметь входной код, который можно легко изменять, то для этого как раз подходит регистр. На рис. 8.3 показана типичная схема включения регистра для хранения кода и временная диаграмма его работы. Код на входе регистра может изменяться произвольным образом, но в тот момент, когда этот код принимает необходимое значение, на вход С триггера подается синхросигнал (строб), который записывает код в регистр. Этот код будет храниться в регистре до прихода следующего строба. Причем важно и то, что все разряды выходного кода регистра будут переключаться одновременно даже в том случае, когда разряды входного кода переключаются не одновременно. Главное, чтобы к приходу положительного фронта строба (сигнала С) все разряды входного кода приняли нужное, устойчивое значение. 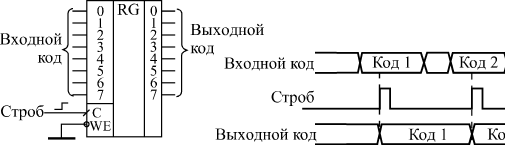 Рис. 8.3. Хранение кода в параллельном регистре Еще одно важнейшее применение регистров связано с запоминанием нескольких последовательных значений изменяющегося входного кода. Это позволяет, например, сравнивать предыдущее значение кода с последующим значением этого же кода или производить арифметические операции над несколькими последовательными значениями одного и того же кода. То есть регистр в данном случае выступает как элемент линии задержки, хранящей в себе историю поведения входного кода. Для примера на рис. 8.4 показана схема вычисления разности двух последовательных значений входного кода. Такая задача возникает, в частности, при цифровой обработке аналоговых сигналов. Последовательные значения входного 4-разрядного кода сопровождаются тактовым сигналом, по положительному фронту которого производится запись в два последовательно включенных регистра. Когда на выходе регистра RG1 присутствует N-ое значение входного кода, на выходе регистра RG2 будет (N–1)-ое значение этого же кода. 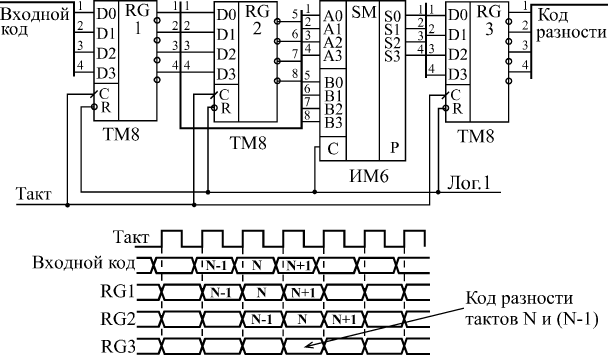 Рис. 8.4. Схема вычисления разности значений кодов в двух последовательных тактах Подавая эти два кода с выходов регистров на 4-разрядный сумматор, включенный в режиме вычитания (см. рис. 8.5), мы получаем на выходе сумматора код разности между N-ым значением и (N–1)-ым значением. В данном случае очень удобен регистр ТМ8, имеющий инверсные выходы. Для обеспечения строго одновременного изменения выходных сигналов сумматора можно включить дополнительный выходной регистр RG3, тактируемый тем же самым общим тактовым сигналом. Правда, код разности при этом будет задержан на один такт. Регистры также широко используются для организации конвейерной обработки, позволяющей существенно повысить тактовую частоту работы схемы. Ускорение при этом достигается за счет распараллеливания работы нескольких последовательно включенных узлов схемы. Пусть, например, последовательность входных кодов, следующих с периодом T, поступает на вход цепочки из двух узлов, производящих обработку или преобразование этих кодов (рис. 8.5). Узлы эти могут представлять собой комбинационные микросхемы (например, сумматоры) или более сложные устройства, включающие в себя микросхемы счетчиков или микросхемы памяти. Главное состоит в том, что выходные сигналы этих узлов выставляются не мгновенно, а в течение какого-то конечного времени, величина которого определяется внутренним строением узла. Пусть задержка установления выходного кода первого узла равняется t1, а задержка установления выходного кода второго узла составляет t2. Очевидно, что период следования входных кодов T не должен быть меньше, чем сумма этих двух задержек: T>t1+t2 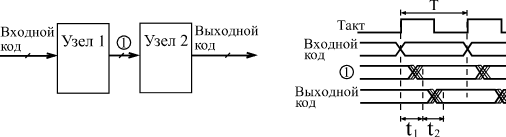 Рис. 8.5. Работа последовательной цепочки двух узлов Иначе код на выходе цепочки может никогда не принять устойчивого значения, так как переходный процесс предыдущего такта будет сменяться переходным процессом следующего такта. То есть быстродействие узлов накладывает жесткое ограничение на тактовую частоту. Однако можно обойти это ограничение, если воспользоваться принципом конвейера, заставить узлы работать не последовательно, а параллельно. Это достигается включением между узлами регистра, тактируемого входным тактовым сигналом. Еще один регистр целесообразно включить на входе второго узла, что обеспечит длительность устойчивого кода на выходе всего устройства, равную длительности периода тактового сигнала Т (рис. 8.6). В результате ограничение на период тактового сигнала становится более мягким: Т не должно быть меньше максимальной из двух величин t1 и t2 с добавлением времени задержки регистра: T>max{t1,t2}+tRG 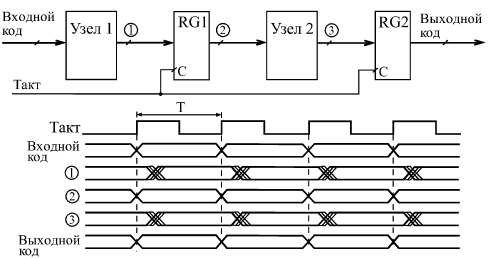 Рис. 8.6. Конвейерная обработка с помощью регистров То есть к следующему фронту тактового сигнала должен закончить свою работу самый медленный из узлов, и тогда его выходной код будет записан в регистр правильно. Точно так же можно построить конвейер на любое количество последовательно включенных узлов. Конечно, в результате введения конвейера происходит задержка выполнения полной функции устройства на число тактов, равное числу введенных регистров. Однако в том случае, когда необходимо обрабатывать большие последовательности входных кодов, эта задержка наблюдается только один раз - в самом начале последовательности, а затем уже она не имеет значения. Регистры могут также применяться в составе вычислителей, выполняя функцию накопителя результата вычисления. В данном случае мы уже имеем дело с более сложной обработкой информации, чем при чисто комбинационных схемах. С каждым тактом в регистре обновляется содержимое, являющееся результатом математической обработки входного кода и результата предыдущего вычисления. Рассмотрим два примера схем таких вычислителей. Первая схема известна как накапливающий сумматор, применяющийся, например, в цифровых генераторах аналоговых сигналов. В самом названии схемы отражена ее функция: она суммирует и накапливает результат. Накапливающий сумматор (рис. 8.7) состоит из сумматора и выходного регистра, охваченных обратной связью. 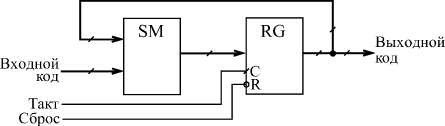 Рис. 8.7. Структура накапливающего сумматора То есть на один вход сумматора подается код с выходов регистра, а на другой вход - входной код. В результате с каждым следующим фронтом тактового сигнала в регистр записывается код суммы входного кода с предыдущим содержимым регистра, с предыдущей суммой. Например, если входной код равен 3, а в регистре записан код 6, то в следующем такте в регистр будет записан код 9 (то есть 6 + 3), в следующем такте - код 12 (то есть 9 + 3) и т.д. Получается, что на выходе накапливающего сумматора формируется равномерно увеличивающийся двоичный код, и шаг этого увеличения можно менять. В данном случае удобно применять регистр со сбросом, например, ИР35. Отметим три особенности накапливающего сумматора. Во-первых, когда выходной код достигает максимальной величины (становится больше 2n, где n - количество разрядов регистра), происходит переполнение схемы и возобновление ее работы с минимальных значений кода. Однако совсем не обязательно в следующем цикле работы будут повторены те же значения кода, что и в предыдущем. Например, пусть n равняется 4, то есть максимальное число на выходе регистра равно 1111 в двоичном коде или 15 в десятичном коде. Пусть входной код равен 3. Тогда после начального сброса регистра выходной код будет нарастать так: 0, 3, 6, 9, 12, 15, 2, 5, 8, 11, 14, 1, 4, .… Это происходит потому, что суммирование чисел 15 и 3 даст 18 или, в двоичном коде, 10010, а так как мы работаем только с младшими четырьмя разрядами, у нас получится 0010 или 2. Во-вторых, особенность накапливающего сумматора состоит в том, что при больших значениях входного кода (больших половины максимально возможной величины) он может рассматриваться как накапливающий вычитатель. Пусть, например, входной код 4-разрядного сумматора равен 15 (1111 в двоичном коде), а в регистре записано число 13 (1011 в двоичном коде). В следующем такте в регистр запишется сумма 1101 + 1111 = 11100, а без старшего разряда - 1100, то есть 12. То есть выходной код уменьшился на единицу. Наконец, в-третьих, совсем не обязательно шаг нарастания выходного кода накапливающего сумматора должен быть целым числом (то есть 0, 1, 2, 3, ...). Если в качестве выходного кода берутся не все, а только старшие разряды регистра, то шаг нарастания вполне может быть дробным, например, 0,5, 1,25 или 3,75. Не вошедшие в выходной код разряды будут иметь вес 2-1 (то есть 0,5), 2-2 (то есть 0,25) и т.д. Правда результат суммирования в выходном коде будет представлен с точностью до целых чисел. При этом возможна ситуация, когда в течение нескольких тактов код на выходе не меняется, например, при входном коде 0,5 выходной код будет меняться один раз на два такта, а при входном коде 0,25 - один раз на четыре такта. 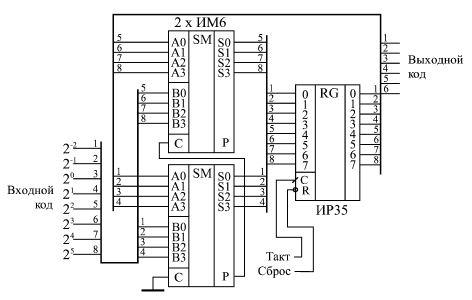 Рис. 8.8. Накапливающий сумматор На рис. 8.8 показана схема 8-разрядного накапливающего сумматора на двух микросхемах сумматоров ИМ6 и одном регистре ИР35. В качестве выходного кода используется только 6 старших разрядов с выхода регистра, поэтому задание шага приращения возможно с точностью до 0,25. Максимально возможная частота тактового сигнала может быть определена по формуле T > tSM + tRG, где Т - период тактового сигнала, tSM - задержка 8-разрядного сумматора, а tRG - задержка регистра. Последний пример применения регистров, который мы рассмотрим, - это вычислитель максимального значения входного кода. Такой вычислитель, например, может применяться в схемах цифровых осциллографов для измерения амплитуды входного аналогового сигнала. Пусть мы имеем последовательность входных кодов, и нам необходимо выявить экстремальный (то есть максимальный или минимальный) код из всей этой последовательности. Эта задача решается довольно просто путем применения компаратора кодов и регистра, охваченных обратной связью (рис. 8.9). 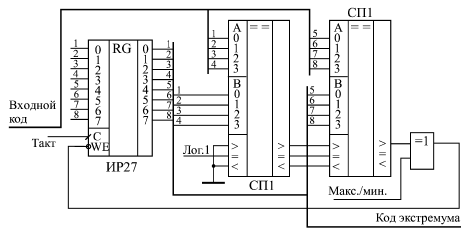 Рис. 8.9. Вычислитель экстремального значения входного кода В данном случае удобно использовать регистр со входом разрешения записи (ИР27). В регистре сохраняется код экстремума (максимума или минимума), а 8-разрядный компаратор, составленный из двух микросхем СП1, сравнивает содержимое регистра и текущее значение входного кода. Элемент Исключающее ИЛИ выполняет функцию управляемого инвертора, выбирая режим вычисления максимума (единица на управляющем входе) или минимума (нуль на управляющем входе). Допустим, мы вычисляем максимум. При этом запись в регистр текущего значения входного кода будет производиться только в том случае, когда это текущее значение больше числа, содержащегося в регистре. На выходе ">" компаратора кодов будет тогда сигнал логической единицы, а на входе разрешения записи регистра –WE - сигнал логического нуля. Если же текущее значение входного кода меньше кода, содержащегося в регистре, запись не производится. После окончания входной последовательности кодов (или после окончания одного ее периода при периодической последовательности) в регистре останется максимальное значение входного кода. Аналогично вычисляется и минимум, только в данном случае в регистр будет записываться не только код, меньший числа в регистре, но и код, равный этому числу. Понятно, что на конечный результат вычисления это никак не повлияет. |
