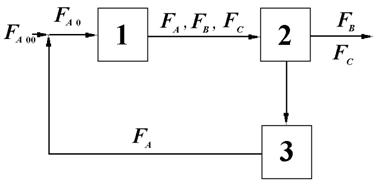
Сборник лекции. Химическая технология - лекция. Лекция Общие вопросы химической технологии. Лекции 2, Принципы создания ресурсосберегающих технологий
 Скачать 1.71 Mb. Скачать 1.71 Mb.
|
|
(1) В нем фигурируют такие показатели производства, как степень конверсии, селективность, объем реактора. Выразив эти показатели количественно, можно найти минимум суммы переменных затрат и минимум себестоимости продукта. Когда способ производства определен или нужно усовершенствовать уже существующую технологию, одним из экономических критериев оптимизации является минимум себестоимости целевого продута. Однако себестоимость сравнительно слабо зависит от производительности и поэтому эффективно использование другого экономического критерия – минимума дохода при прибыли где FB – производительность (мощность) по товарному продукту В, ЦВ – его оптовая цена, СВ – его заводская себестоимость. Прибылью определяется рентабельность производства, являющаяся одним из основных показателей экономической эффективности. Очевидно, что при FB = const максимум дохода достигается при минимуме себестоимости. Наконец, при оценке разных методов производства или способов организации отдельных его стадий важнейшим экономическим критерием оптимальности является минимум приведенных затрат где Е – отраслевой нормативный коэффициент эффективности капитальных вложений, равный обратной величине срока их окупаемости (для химической и нефтехимической промышленности Е = 0,15-0,25); Куд. – удельные капитальные вложения на единицу продукции. Как и стоимость оборудования, Куд. изменяется в дробной степени от их объема. В полученных уравнениях переменных затрат себестоимости и прибыли отдельные слагаемые являются функцией таких параметров как начальные парциальные давления (или концентрации) степень конверсии и т.д. Проведя соответствующие замены и найдя положение экстремума переменных затрат себестоимости или прибыли, можно найти оптимальные параметры процесса. Многие из них влияют и на селективность процесса. В данном случае мы рассмотрим лишь некоторые простейшие задачи, связанные с изменением только удельной производительности реактора. Одна из них состоит в выборе оптимальных количеств гомогенного катализатора, инициатора или интенсивности излучения, когда увеличение затрат на интенсификацию процесса противопоставляется снижению объема и стоимости реактора. Пример. Реакция А В проводится в аппарате полного смешения в присутствии гомогенного катализатора. Определить его оптимальную концентрацию, если кинетическое уравнение реакции моль/(лч), k = 20 моль/(лч), степень конверсии ХА = 0,95, стоимость катализатора ЦК = 4 руб/кмоль, а отчисления не амортизацию выражается уравнением Решение. Затраты на катализатор составляют руб/ч Объем реактора находим из уравнения для рис. откуда Оптимизации подлежит сумма  При заданном FB и ХА для нахождения минимума берем производную приравниваем ее нулю 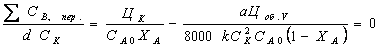 откуда 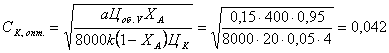 моль/л моль/лИз общего вида выражения для СК, опт. Очевидно, что оптимальная концентрация катализатора тем больше, чем выше степень конверсии и цена реактора, а также чем ниже константа скорости и цена катализатора. При заданной мощности производства оптимизация по критерию максимального дохода дает такие же результаты. Однако для действующей установки с известным объемом реактора с возможностью варьирования его мощности (FB) результаты получаются иными. Это объясняется тем, что постоянные во времени амортизационные отчисления станут переменными в расчете на единицу продукции. Пример. Найти для предыдущего примера по критерию себестоимости оптимальную концентрацию катализатора, если все условия останутся прежними, но FB и FB могут изменяться, а Цоб., 0 = 1500 руб и V = 4 м3. Решение. В данном случае минимизации подлежит сумма 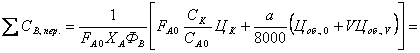 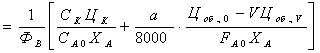 При известном объеме реактора 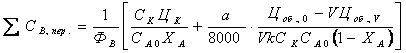 При постоянных ФВ, СА 0, ХА находим производную и приравниваем ее нулю. 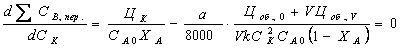 откуда 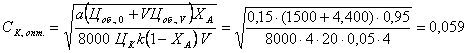 моль/л моль/лСледовательно, становится более выгодным повышение концентрации катализатора, т.е. некоторая интенсификация процесса, что еще сильнее проявляется при использовании критерия максимального дохода. Влияние единичной мощности оборудования на экономические показатели. Ранее указывалось, что расходы на заработную плату, амортизационные отчисления и удельные капитальные вложения растут в дробной степени от величины потоков или объема оборудования. Это же относится и к непроизводственным потерям сырья и продукции. Таким образом, при прочих равных условиях себестоимость снижается при увеличении единичной мощности любого оборудования, в том числе и реактора. Поэтому понятна современная тенденция увеличения мощности установок от 10-60 до 100-600 тыс. т. в год и более по целевым продуктам. Одновременно во избежание роста удельных капитальных вложений устраняются запасные технологические нитки производства и дублируются лишь отдельные виды оборудования, более ответственные, либо требующие более частного ремонта. Все это обусловлено необходимость резкого повышения надежности работы оборудования. Оптимальные концентрации инициатора и температуры в радикально-цепных реакциях В радикально-цепных процессах с квадратичным обрывом цепей и химическим инициированием имеется оптимум концентрации инициатора и температуры реакции. Это объясняется тем, что скорость распада инициатора описывается уравнением первого порядка по инициатору , а общая скорость реакции имеет по нему половинный порядок, например где , k – константа скорости лимитирующей стадии продолжения цепи, kt – константа скорости обрыва цепи. Делением этих выражений друг на друга получаем дифференциальное уравнение 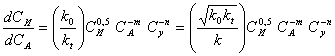 Это уравнение показывает, что удельный расход инициатора растет с повышением его концентрации и отношения . Обычно энергия активации обрыва цепи равна нулю, для k она невелика и составляет около 20 кДж/моль, а для стадии распада инициатора достигает 100-120 кДж/моль. Следовательно, для комплекса констант энергия активации величина положительная, а значит, удельный расход инициатора растет с повышением температуры. С другой стороны, снижение концентрации инициатора и температуры ведет к снижению интенсивности процесса и росту затрат на капитальные вложения и амортизацию реакционного узла. Противопоставление этих расходов неизбежно приводит к некоторому оптимуму по концентрации инициатора и температуре. Пример. Реакцию A + Y В проводят в жидкой фазе в реакторе идеального смешения в присутствии инициатора. Реагент А является растворителем, а Y – газом, барбатируемым через жидкость, вследствие чего их концентрации постоянны. Т.о., реакция имеет псевдопервые порядки по реагентам и ее скорость описывается уравнением При 350К константы и равны , , а энергия активации и . Определить оптимальные концентрации инициатора и температуру реакции, если оптовая цена инициатора ЦИ = 100 руб/кмоль, амортизационные отчисления по реакционному узлу описываются уравнением где , степень конверсии инициатора XИ = 0,90 и степень конверсии реагента XА = 0,25 при . Решение. Из дифференциального уравнения удельного расхода инициатора получаем для реактора идеального смешения и заданной кинетики процесса Отсюда начальная концентрация инициатора, обеспечивающая заданную степень конверсии XА будет равна  Для ее расчета находим , , и для ряда температур через пятиградусные интервалы по уравнению
Из часового экономического баланса находим уравнение для суммы переменных затрат 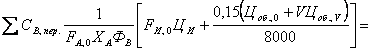 При заданной мощности по целевому продукту и селективности второе слагаемое уравнения постоянно и минимизации подлежит сумма двух других. Объем реактора находим по известному выражению 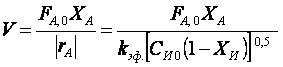 что окончательно дает 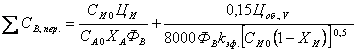 Оптимум при постоянной селективности не зависти от ФВ. Поэтому рассчитываем при ФВ = 1 найденным значениям kэф. и СИ 0 при разных температурах.
Построив графическую зависимость от Т, находим, что минимум себестоимости достигается при температуре 338К и начальной концентрации инициатора 0,0129 моль/л. В действительности задача оптимизации температуры реакции и концентрации инициатора является более сложной. Так чтобы снизить расход обычно дорогостоящего инициатора в периодических условиях в реакторах идеального вытеснения или в каскаде реакторов, выгодно поддерживать постепенно повышающийся профиль температуры. Удельный расход инициатора при значительных его концентрациях снижается за счет уменьшения температуры, производительность реактора на завершающих этапах увеличивается за счет постепенного повышения температуры. Из рассмотренных уравнений видно, что степень превращения реагента также влияет на удельный расход инициатора и может использоваться как взаимозаменяемый параметр с температурой и концентрацией инициатора. Оптимизация степени конверсии. Эта задача часто является одной из важнейших, поскольку степень конверсии сильно влияет на удельную производительность реакторов, и на селективность. При оптимизации степени превращения необходимо рассматривать вместе расходы по реакционному узлу и по смежным стадиям отделения непревращенного реагента и системы его рециркуляции. Последние два включают энергетические затраты (работа колонны разделения, компрессоров, насосов, теплообменников), а также возможные непроизводственные потери сырья, зависящие от величины рециркулирующих потоков. При прочих равных условиях можно принять, что упомянутые энергетические затраты пропорциональны величине рециркулирующего потока. Кроме того в сложных реакциях побочный продукт может иметь определенную ценность и его следует включать в уравнение экономического баланса. Пример. Целевой продукт В получают в последовательных реакциях первого порядка в изотермических условиях в реакторе идеального вытеснения объемом 2,5 м3. Из экспериментальных данных известно, что k1= 0,1 ч-1 и , оптовая цена за катализатор равна ЦА = 20 руб/кмоль. Энергетические затраты на выделение и рециркуляцию непрореагировавшего вещества А составляют 3 руб/кмоль, амортизационные отчисления по реакционному узлу стадии отделения непрореагировавшего вещества А и его рециркуляцию описываются уравнением СА 0 = 2 моль/л. Найти оптимальную степень конверсии в условиях рециркуляции непрореагировавшего иещества А, если 1) побочный продукт является бесполезным отходом; 2) побочный продукт утилизируется и его товарная цена составляет 7 руб/кмоль.
Решение. Из схемы потоков видно, что , откуда В соответствии с кинетикой процесса, получим для реактора идеального вытеснения 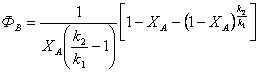 . .Часовой экономический баланс по переменным затратам в общем виде определяется как откуда сумма переменных слагаемых себестоимости составляет Подставляя в последнее уравнение выражения
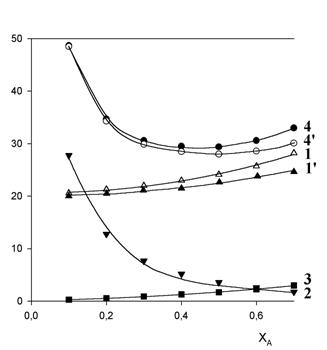
Графическое изображение полученных данных представлено на рисунке
Можно видеть, что материальные затраты ( |