статистика. статистика учебное пособие. Лекция Предмет и метод статистики Предмет, метод и основные категории статистики как науки Слово статистика
 Скачать 1.29 Mb.
|
|
Причины применения выборочного метода: Если достаточно приблизительной оценки обобщающего показателя, то такую оценку можно вычислить и по выборке, что будет гораздо дешевле и быстрее, чем организация сплошного наблюдения. Если генеральная совокупность очень велика или бесконечна, то сплошное обследование невозможно. Иногда даже при конечной генеральной совокупности выборочный метод является единственно возможным. Например, при контроле качества продукции, если проверка сопровождается уничтожением образца. Бывает, что генеральная совокупность уже не существует. Такая ситуация имеет место в задачах, связанных с анализом динамических рядов, описывающих доходы, уровень производства, занятость за прошлый период. Все эти данные можно восстановить только выборочным путем. Результаты выборочного статистического исследования во многом зависят от уровня подготовки процесса наблюдения. Под уровнем подготовки в данном случае подразумевается соблюдение определенных правил и принципов проектирования выборочного обследования. Важнейшим элементом проектирования является составление организационного плана выборочного наблюдения. В общем виде в организационный планвключаются следующие вопросы: Постановка цели и задачи наблюдения. Определение границ объекта исследования. Отработка программы наблюдения (составление анкеты, опросного листа, формы отчета и т. д.) и разработка ее материалов. Определение процедуры отбора, способа отбора и объема выборки. Подготовка кадров для проведения наблюдения, размножение формуляров, инструктивных документов и др. Расчет выборочных характеристик и определение ошибок выборки. Распространение выборочных данных на всю совокупность. Специфические вопросы организационного плана выборочного статистического наблюдения будут рассмотрены ниже. Состав выборочной совокупности может отличаться от состава генеральной совокупности. Это расхождение между характеристиками выборки и генеральной совокупности составляет ошибку выборки. Ошибка зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, методов отбора единиц в выборку. Основная задача выборочного обследования состоит в том, чтобы на основе характеристик выборочной совокупности получить достоверные суждения о показателях, характеризующих генеральную совокупность. Обычно применяют способ прямого пересчета, который состоит в том, показатели выборочной совокупности распространяют и на генеральную совокупность. Ошибка выборки при этом определяется с помощью методов математической статистики. Способы формирования выборочной совокупности При формировании выборки исследователь стремится, чтобы выборка была репрезентативной (представительной), т.е. достаточно хорошо отображала свойства генеральной совокупности. Если отбор элементов производится произвольно, то полученная выборка носит название случайной. В математической статистике это понятие имеет специальное определение: выборка называется случайной, если все элементы генеральной совокупности имеют одинаковые вероятности быть отобранными в состав этой выборки. Это соответствует процедуре взятия выборки с возвратом, или повторному отбору. При повторном отборе каждая единица после фиксации значения изучаемого признака должна быть возвращена в генеральную совокупность, где ей опять предоставляется равная возможность попасть в выборку. Но на практике повторный отбор осуществляется редко. Обычно выборочные исследования проводятся по схеме бесповторного отбора, при котором повторное попадание в выборку одних и тех же единиц исключено. Если генеральная совокупность велика, а объем выборки относительно мал, между повторным и бесповторным отбором нет разницы. В противном случае, если объем выборки составляет более 5 % объема генеральной совокупности, бесповторный отбор приведет к существенно иным результатам. Бесповторный отбор дает более точные результаты по сравнению с повторным, т.к. при одном и том же объеме выборки охватывается большее количество единиц генеральной совокупности. Однако бесповторный отбор при большом объеме генеральной совокупности не всегда целесообразен. Например, при исследовании пассажиропотоков или изучении потребительского спроса целесообразнее применять повторный отбор. В статистике применяются различные способы формирования выборочной совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения. Основным условием проведения выборочного обследования является предупреждение возникновения систематических ошибок, возникающих вследствие нарушения равных возможностей попадания в выборку каждой единицы генеральной совокупности. Практика применения выборочного метода в экономико-статистических исследованиях использует индивидуальный, групповой и комбинированный способы отбора в выборочную совокупность. В случае индивидуального отбора в выборку отбираются отдельные единицы генеральной совокупности, в случае группового - качественно однородные группы или серии изучаемых единиц. Комбинированный отбор является комбинацией индивидуального и группового способов отбора из генеральной совокупности. По правилам формирования выборочной совокупности выделяются выборки: собственно случайная; механическая; экспертная; типическая; серийная; комбинированная. Собственно случайный отбор. Собственно случайный отбор является наиболее простым способом формирования выборочной совокупности. Выборка образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности, при этом предполагается, что в распоряжении исследователя имеется полный перечень единиц (рис. 2.4). Количество отобранных в выборочную совокупность единиц определяется исходя из принятой доли выборки как отношение числа единиц выборочной совокупности к численности единиц генеральной совокупности. Так при 5%-й выборке из партии в 2000 единиц численность выборки составляет 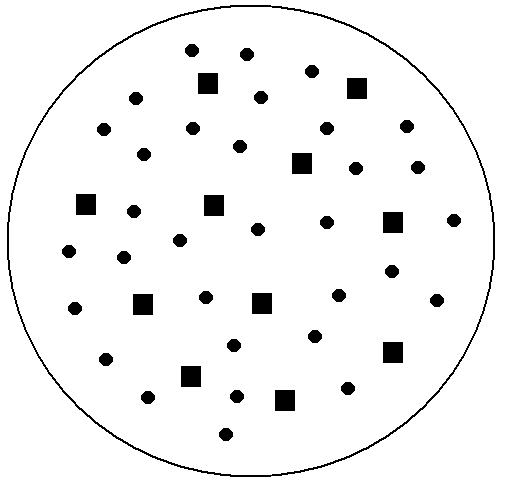 единиц. Рис. 2.4. Собственно случайная выборка Важным условием собственно случайной выборки является то, что каждой единице генеральной совокупности предоставляется равная возможность попасть в выборку. Именно принцип случайности попадания любой единицы в выборку предупреждает возникновение систематических ошибок. Примером использования собственно-случайной выборки является проведение тиражей лотереи, при которых обеспечивается равная возможность попадания в тираж любого номера лотерейного билета. Формирование собственно случайной выборки обычно осуществляется с помощью специальных фишек или таблиц случайных чисел. В случае использования фишек все единицы генеральной совокупности нумеруются и каждый номер записывается на фишку (жребий) одинаковой формы. Фишки тщательно перемешиваются и отбираются в выборку по одной. При использовании таблиц случайных чисел из таблицы выбирается любая строка или колонка таблицы и выборку включаются указанные номера единиц генеральной совокупности. Собственно случайная выборка может быть повторной и бесповторной. Так как при повторном отборе каждая единица, попавшая в выборку, после ее обследования должна обязательно быть возвращена в генеральную совокупность, на практике это не всегда осуществимо. Например, после контроля качества электроламп на продолжительность горения, нет никакого смысла возвращать в генеральную совокупность перегоревшие лампочки. А вот в случае изучения покупательского спроса населения допускается повторная регистрация неудовлетворенного спроса одного и того же лица в нескольких магазинах города. Механический отбор. Процедура механического отбора намного проще собственно случайного отбора, поэтому механический отбор на практике используется более широко и основан на предварительном упорядочении генеральной совокупности. Отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). Размер интервала равен обратной величине доли выборки. Так при 2 %-й выборке отбирается каждая  единица.Таким образом, генеральная совокупность механически разбивается на равновеликие группы. Из каждой такой группы в выборку отбирается лишь одна единица. Например, из телефонной книги берем каждую десятую фамилию, спрос в магазинах изучаем по пятницам и т.д. Для обеспечения репрезентативности выборки все единицы генеральной совокупности должны располагаться в определенном порядке. При этом по отношению к изучаемому показателю единицы генеральной совокупности могут быть упорядочены по существенному, второстепенному или нейтральному признакам. При упорядочении генеральной совокупности по существенному признаку – признаку, всецело определяющему поведение изучаемого показателя – в выборочную совокупность должна отбираться та единица, которая находится в середине каждой группы (рис. 2.5). Это позволяет избежать появления систематической ошибки выборки. Например, при изучении выполнения нормы выработки кассирами составляется список, упорядоченный по возрастанию показателя выполнения норм. При 10 %-м выборочном обследовании из каждого десятка в выборку следует отбирать пятые или шестые номера. Если в выборку отбирать первые номера из каждого десятка, то это исказит (занизит) выборочные характеристики – появится систематическая ошибка репрезентативности. При упорядочении генеральной совокупности по нейтральному признаку – признаку, который не влияет на поведение изучаемого показателя, – в выборочную совокупность из первой группы генеральной совокупности может быть взята любая единица. Во всех последующих группах механической выборки берут единицы, соответствующие порядковому номеру единицы, отобранной в первой группе, для соблюдения принципа случайности отбора. 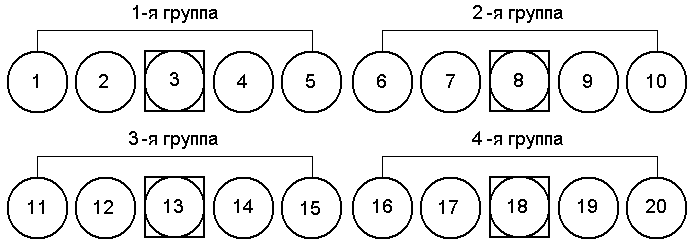 Рис. 2.5. Механическая выборка В основе упорядочения единиц генеральной совокупности может лежать и второстепенный по отношению к изучаемому показателю признак. Например, при исследовании хлебобулочных изделий в качестве признака, упорядочивающего совокупность, выбирается последовательность выхода продукции из цеха, но к концу смены качество может измениться под влиянием таких факторов, как разладка машин, усталость работников и т.д. В этом случае следует учитывать второстепенные признаки и выбирать из каждой группы единицы, находящиеся в ее середине. Важной особенностью механической выборки является то, что формирование выборки можно осуществлять, не прибегая к составлению списков. На практике используют тот порядок, в котором фактически размещаются единицы генеральной совокупности. Если элементы генеральной совокупности хорошо перемешаны, между механической и собственно случайной выборками не будет большой разницы. Если же элементы генеральной совокупности расположены в определенном порядке, то механического отбора следует избегать из-за возможного появления систематических ошибок. Например, нельзя проверять только дома с четными номерами или каждую 4-ю квартиру в доме, или посещаемость студентами занятий каждую пятницу. Экспертный отбор. При этом отборе исследователь сам решает, какой элемент генеральной совокупности попадает в выборку. Такой отбор можно применять лишь при отборе небольших выборок и из небольших генеральных совокупностей. Чаще всего экспертный отбор применяется при покупке и продаже товаров. Покупатели фруктов, кофе и многих других товаров постоянно основывают свои решения на экспертном отборе. Если исследователь обладает знаниями и опытом, он сможет получить очень хорошие оценки (лучше, чем при собственно случайном отборе) при очень маленьких выборках. Типический отбор. При типическом отборе генеральная совокупность вначале разбивается на однородные типические группы. Выбор из каждой типической группы осуществляется собственно случайным или механическим способом (рис. 2.6). 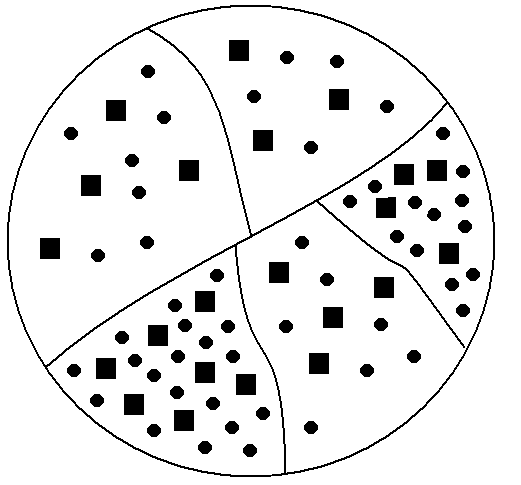 Рис.2.6. Типическая выборка Типическая выборка применяется при изучении сложных статистических совокупностей, например, при выборочном обследовании производительности труда работников торговли, состоящих из отдельных групп по квалификации; при проведении бюджетных обследований домашних хозяйств, сгруппированных по источнику средств существования или уровню образования. Число единиц из каждой выделенной группы отбирается в зависимости от числа элементов в каждой группе. Существует три способа отбора: Отбор из каждой группы равного числа единиц дает достаточно надежные результаты лишь при равных размерах выделенных типических групп. Отбор единиц пропорционально их численности в соответствующих группах генеральной совокупности. Использование этого способа формирования выборочной совокупности обеспечивает достаточно надежные результаты, если колеблемость признака несущественно различается в разных группах генеральной совокупности. Если же коэффициенты вариации в них различаются, то репрезентативность выборки при таком способе может оказаться невысокой. Оптимальное размещение, учитывающее не только численность групп, но и степень вариации в них изучаемого признака. Разновидностью типической является районированная выборка, при которой отбор единиц для наблюдения проводится из групп, представленных административно-территориальными образованиями. В этом случае преимущества типической выборки проявляется лишь при заметном расхождении среднего значения изучаемого признака по отдельным регионам. Серийный (гнездовый) отбор. Серийный отбор применяется, если генеральная совокупность разбита на группы еще до начала выборочного обследования (рис. 2.7) и довольно широко используется в торговле. 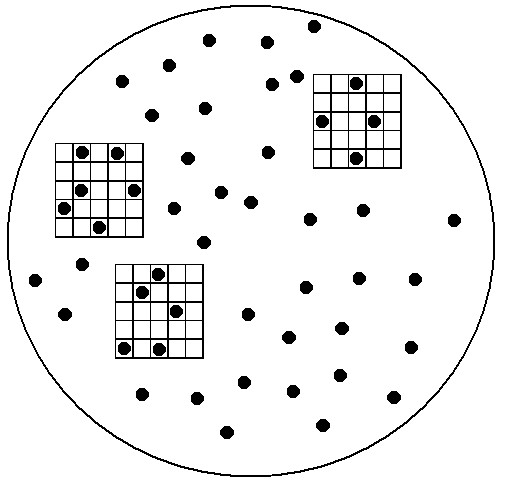 Рис. 2.7. Серийная выборка При серийной выборке из генеральной совокупности отбираются не отдельные единицы, а целые их серии (гнезда). Внутри же каждой из попавшей в выборку серии обследуются все без исключения единицы, т.е. применяется сплошное наблюдение. Отбор отдельных серий в выборку осуществляется либо собственно случайным, либо механическим способом. Применение серийного отбора обусловлено тем, что многие товары упаковываются в пачки, коробки, ящики и т.п. При контроле качества товара рациональнее проверить несколько отдельных упаковок (серий), чем из всех упаковок отобрать необходимое количество единиц товара. В рассмотренных способах формирования выборочной совокупности отбор единиц для наблюдения осуществляется на первом этапе. Такой отбор называется одноступенчатым. На практике же используется многоступенчатый отбор, когда на первом этапе из совокупности отбираются укрупненные единицы (серии), а затем в рамках серии осуществляется собственно случайный или механический отбор единиц из каждой отобранной серии. При построении многоступенчатой выборки используется комбинация разных способов отбора – комбинированная выборка. Моментные или выборочные исследования. Этот способ применяется для статистического изучения протекающих во времени процессов. Большое распространение способ получил при анализе использования рабочего времени. Моментные выборочные исследования менее трудоемки, чем хронометраж рабочего дня, а результаты при правильной организации моментных обследований достаточно точны. Основным содержанием способа является периодическая фиксация (в заранее установленные моменты времени) состояния изучаемой совокупности. При сплошном охвате всех единиц совокупности этот способ по времени получения информации. Лекция 3. Сводка и группировка данных статистического наблюдения 3.1. Понятия сводки и группировки статистических данных Собранный в процессе статистического наблюдения материал нуждается в определенной обработке, сведении разрозненных данных воедино. Научно организованная обработка материалов наблюдения (по заранее разработанной программе), включающая в себя кроме обязательного контроля собранных данных систематизацию, группировку материалов, составление таблиц, получение итогов и производных показателей (средних, относительных величин), называется в статистике сводкой. Сводка представляет собой второй этап статистического исследования. Целью сводки является получение на основе сведенных материалов обобщающих статистических показателей, отражающих сущность социально-экономических явлений и определенные статистические закономерности. Статистическая сводка осуществляется по программе, которая должна разрабатываться еще до сбора статистических данных, практически одновременно с составлением плана и программы статистического наблюдения. Программа сводки включает определение групп и подгрупп; системы показателей; видов таблиц. Группировка – это разбиение совокупности на группы, однородные по какому-либо признаку. С точки зрения отдельных единиц совокупности группировка – это объединение отдельных единиц совокупности в группы, однородные по каким-либо признакам. Устойчивое разграничение объектов выражается классификацией, которая основывается на самых существенных признаках (например, классификация отраслей народного хозяйства, классификация основных фондов и т.д.). Таким образом, классификация – это узаконенная, общепринятая, нормативная группировка. Метод группировки основывается на следующих категориях – это группировочный признак, интервал группировки и число групп. Группировочный признак – это признак, по которому происходит объединение отдельных единиц совокупности в однородные группы. Интервал очерчивает количественные границы групп. Как правило, он представляет собой промежуток между максимальными и минимальными значениями признака в группе. Интервалы бывают: равные, когда разность между максимальным и минимальным значениями в каждом из интервалов одинакова; неравные, когда, например, ширина интервала постепенно увеличивается, а верхний интервал часто не закрывается вовсе; открытые, когда имеется только либо верхняя, либо нижняя граница; закрытые, когда имеются и нижняя, и верхняя границы. Определение числа групп. Здесь необходимо учитывать несколько условий: а) число групп детерминируется уровнем колеблемости группировочного признака. Чем значительнее вариация признака, тем больше при прочих равных условиях должно быть групп; б) число групп должно отражать реальную структуру изучаемой совокупности; в) не допускается выделение пустых групп. Если проблема пустых групп все же возникает, при проведении структурных группировок используют неравные интервалы. Для нахождения числа групп служит формула  где N – количество элементов совокупности. В случае равных интервалов величина интервала может быть определена как 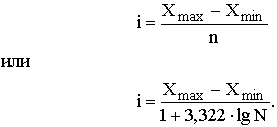 3.2. Виды группировок. При проведении группировки приходится решать ряд задач: 1) выделение группировочного признака; 2) определение числа групп и величины интервалов; 3) при наличии нескольких группировочных признаков описание того, как они комбинируются между собой; 4) установление показателей, которыми должны характеризоваться группы, т.е. сказуемого группировки. Статистические группировки и классификации преследуют цели выделения качественно однородных совокупностей, изучения структуры совокупности, исследования существующих зависимостей. Каждой из этих целей соответствует особый вид группировки: типологическая, структурная, аналитическая (факторная). Типологическая группировка решает задачу выявления и характеристики социально-экономических типов (частных подсовокупностей). Структурная дает возможность описать составные части совокупности или строение типов, а также проанализировать структурные сдвиги. Аналитическая (факторная) группировка позволяет оценивать связи между взаимодействующими признаками. В зависимости от числа положенных в их основание признаков различают простые и многомерные группировки. Группировка, выполненная по одному признаку, называется простой. Многомерная группировка производится по двум и более признакам. Частным случаем многомерной группировки является комбинационная группировка, базирующаяся на двух и более признаках, взятых во взаимосвязи, в комбинации. Структурная группировка применяется для характеристики структуры совокупности и структуры сдвигов. Структурной называется группировка, в которой происходит разделение выделенных с помощью технологической группировки типов явлений, однородных совокупностей на группы, характеризующие их структуру по какого либо варьирующему признаку. Например, группировка населения по размеру среднедушевого дохода. Анализ структурных группировок взятых за ряд периодов или моментов времени, показывает изменения структуры изучаемых явлений, то есть структурные сдвиги. В изменении структуры общественных явлений отражаются важнейшие закономерности их развития. Показатель численности групп представлен либо частотой (количеством единиц в каждой группе), либо частотностью (удельным весом каждой группы). Среди простых группировок особо выделяют ряды распределения. Ряд распределения – это группировка, в которой для характеристики групп (упорядоченно расположенных по значению признака) применяется один показатель – численность группы. Другими словами, это ряд чисел, показывающий, как распределяются единицы некоторой совокупности по изучаемому признаку. Ряды, построенные по атрибутивному признаку, называются атрибутивными рядами распределения. Ряды распределения, построенные по количественному признаку, называются вариационными рядами. Примером атрибутивных рядов могут служить распределения населения по полу, занятости, национальности, профессии и т.д. Примером вариационного ряда распределения могут служит распределения населения по возрасту, рабочих – по стажу работы, заработной плате и т.д. Вариационные ряды распределения состоят их двух элементов вариантов и частот. Вариантами называются числовые значения количественного признака в ряду распределения, они могут быть положительными и отрицательными, абсолютными и относительными. Частоты – это численности отдельных вариантов или каждой группы вариационного ряда. Сумма всех частот называется объемом совокупности и определяет число элементов всей совокупности. Вариационные ряды в зависимости от характера вариации подразделяются на дискретные и интервальные. Результаты сводки и группировки материалов статистического наблюдения оформляются в виде статистических рядов распределения и таблиц. Статистические ряды распределения представляют собой упорядоченное расположение единиц изучаемой совокупности по группировочному признаку. Ряды распределения, образованные по качественным признакам, называют атрибутивными. При группировке ряда по количественному признаку получаются вариационные ряды. Вариационные ряды бывают дискретными, основанными на дискретном признаке, и интервальными, основанными на непрерывно изменяющемся значении признака. Применяются также интервальные ряды распределения. При их построении возникают вопросы о числе групп, величине интервала, его границе. Дискретные вариационные ряды. Пусть  - возможные значения дискретного признака, при этом  . Исследуемая статистическая совокупность содержит статистические единицы. В этой совокупности  единиц имеют значение признака  ,  единиц -  , ... ,  единиц -  . Числа  называются абсолютными частотами.Если  - общее количество единиц совокупности, то  ,  .Обычно при статистическом исследовании вместо абсолютных рассматриваются относительные частоты:  .Для них выполняются соотношения:  ,  .Интервальные вариационные ряды. Пусть исследуемый признак может принимать значения из непрерывного промежутка  . Произведем группировку данных. Выберем интервалы  . Обычно заранее решают, к какой именно группе относить границы интервалов  (например, пусть интервал включает свою верхнюю границу, тогда получаем интервалы  ). Подсчитывается число объектов, попавших в каждый из интервалов, и рассчитываются относительные частоты.Интервалы группировок выделяют из логических соображений. Иногда используются "принцип равных интервалов", о котором говорилось выше, и "принцип равных частот", по которому интервалы выбираются таким образом, чтобы относительные частоты были примерно одинаковы. 3.3. Статистические таблицы и графики Результаты сводки и группировки материалов наблюдения, как правило, представляются в виде статистических таблиц. Это наиболее рациональная форма представления результатов статистической сводки. Статистическая таблица – это форма краткого и рационального изложения сводной числовой характеристики исследуемой совокупности по одному или нескольким существующим признакам, взаимосвязанным логикой экономического анализа. Таблицей называется такая форма представления числовой информации, при которой число располагается на пересечении четко сформулированного заголовка по вертикальному столбцу (графе) и названия по соответствующей горизонтальной полосе (строке). Внешне таблица представляет собой пересечение граф и строк, которые формируют остов таблицы. Составленную таблицу, но не заполненную цифрами, называют макетом таблицы или пустографиком, в котором мысленно определяются в деталях цель обследования и объем разработки материалов сводки. Статистическая таблица содержит три вида заголовков: общий, верхние, боковые. Общий заголовок отражает содержание всей таблицы, располагается над макетом таблицы по центру и является внешним заголовком. Верхние заголовки характеризуют содержание граф (заголовки сказуемого), боковые – строк (заголовки сказуемого) и являются внутренними заголовками (рис. 3.1). Название таблицы(общий заголовок)
*) Примечания к таблице Рис. 3.1. Остов статистической таблицы Каждая статистическая таблица содержит подлежащее и сказуемое. Подлежащим таблицы называется объект, отдельные единицы или группы, которые характеризуются соответствующими показателями. Сказуемым таблицы называются показатели, с помощью которых изучается подлежащее таблицы. В основном в сказуемом отражаются численные значения и характеристики изучаемого явления. Подлежащее таблицы обычно составляет название ее строк и располагается в левой части таблицы. Сказуемое формирует заголовки граф (колонок) и составляет их содержание. Иногда, в целях получения более компактной таблицы подлежащее и сказуемое меняют местами, т.е. подлежащее указывают по графам, а сказуемое – по строкам. Статистические таблицы классифицируются по способу построения подлежащего и сказуемого (рис. 3.2). 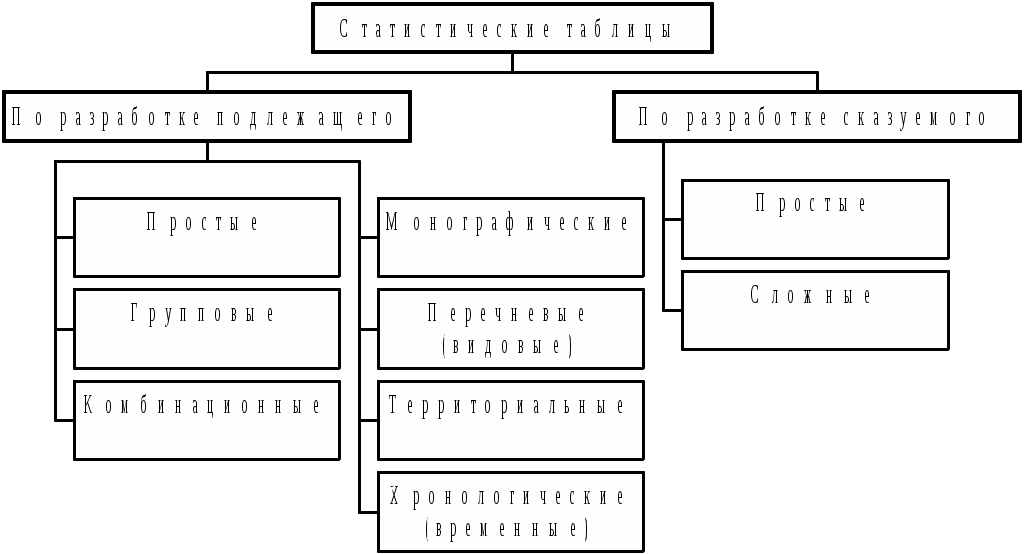 Рис. 3.2. Классификация статистических таблиц Простые таблицы получили большое распространение во многих экономических разработках. Подлежащее простой таблицы представляет собой перечень отдельных единиц изучаемого объекта. По характеру представляемого материала эти таблицы бывают собственно монографические, перечневые, территориальные и хронологические. Монографическая таблица содержит в подлежащем одну какую-либо единицу, выделенную по определенному признаку (табл. 3.1). Подлежащим в табл. 3.1 являются государственные краткосрочные облигации (ГКО). Перечневая или построенная по видовому принципу таблица в подлежащем содержит перечисление единиц изучаемой совокупности (табл. 3.2). Таблицы, в подлежащем которых приводится перечень территорий (районов, областей и т.п.), называются территориальными (табл. 3.3). Для оценки изменения во времени разрабатываются хронологические или построенные по временному принципу таблицы, в подлежащем которых приводятся периоды времени или даты, а в сказуемом - ряд показателей. Хронологическую таблицу можно составлять за любые по величине отрезки времени или на моменты, отстающие друг от друга по времени на различную длину (табл. 3.4). Таблица 3.1 Характеристика выпуска государственных краткосрочных облигаций РФ в 1995 г.
Таблица 3.2 | ||||||||||||||||||||||||||||||||||||||||||||||||