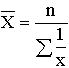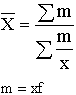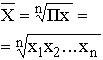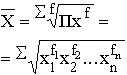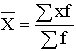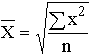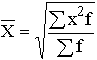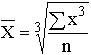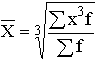статистика. статистика учебное пособие. Лекция Предмет и метод статистики Предмет, метод и основные категории статистики как науки Слово статистика
 Скачать 1.29 Mb. Скачать 1.29 Mb.
|
|
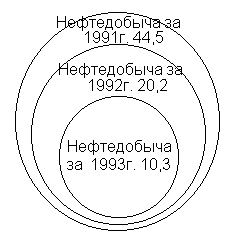
Широкое применение в статистике находят диаграммы, позволяющие отразить структуру совокупности, ее изменение и динамику численности данной совокупности (рис. 3.9). Для построения таких диаграмм ряд абсолютных показателей совокупности заменяется рядом относительных величин. Наиболее распространенным видом таких диаграмм являются секторные диаграммы. В этих диаграммах площадь окружности принимается за величину всей изучаемой статистической совокупности, а площади отдельных секторов отображают удельный вес (долю) ее составных частей. Так как площади секторов пропорциональны центральным углам, то сумма всех углов (360 градусов) распределяется пропорционально удельным весам отдельных частей изучаемой совокупности. 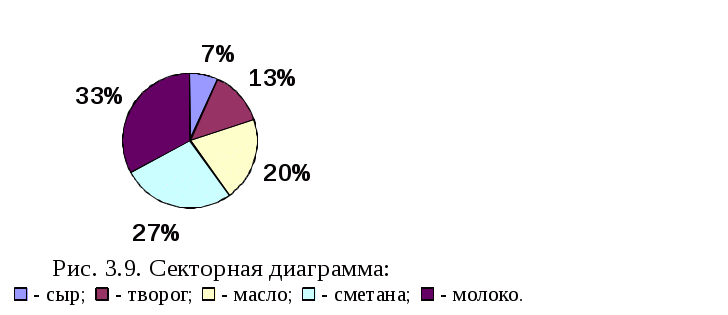 К недостаткам секторной диаграммы следует отнести малую эффективность при большом числе частей совокупности и снижение наглядности при незначительных изменениях структуры изображаемых совокупностей. Другим видом диаграмм, отображающих структуру совокупности, являются столбиковые и полосовые диаграммы, в качестве графического образа в которых используются прямоугольники (рис. 3.10). Каждая из полос диаграммы будет иметь одинаковую длину, так как при переходе к относительным величинам погашаются различия в абсолютных размерах совокупностей. 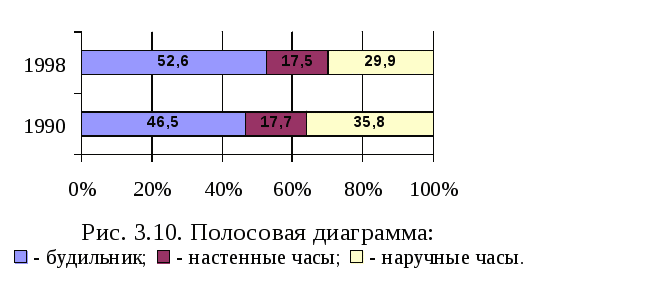 Наглядным изображением статистической информации являются столбиковые диаграммы (рис. 3.11). При построении столбиковых диаграмм также используется прямоугольная система координат. Каждое значение изучаемого показателя изображается в виде вертикального столбика. По оси абсцисс размещается основание столбиков. Их ширина может быть произвольной, но обязательно одинаковой для каждого столбика. Высота столбиков (в соответствии с принятым по оси ординат масштабом) должна строго соответствовать изображаемым данным. Количество столбцов определяется числом данных. Расстояние между столбиками должно быть одинаковым. У основания столбиков дается название изучаемого показателя. Значения показателей помещаются внутри каждого столбика. Из рис. 3.11 видно, что отсутствие информации за 1981-1984 гг. на технику построения столбиковой диаграммы не повлияло. При этом важно, чтобы все данные по приведенным годам располагались в хронологической последовательности. В статистике находят применение и так называемые ленточные (полосовые) графики (рис. 3.12). В этих диаграммах основания располагаются вертикально, а масштабная шкала наносится на горизонтальную ось. Ленточная диаграмма представляет собой ряд простирающихся по оси абсцисс лент одинаковой ширины. При построении ленточных диаграмм соблюдаются те же требования, что и при построении столбиковых графиков (одинаковая ширина полос, начало шкалы от нулевой отметки и др.). 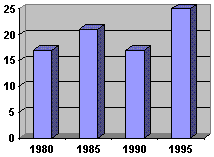 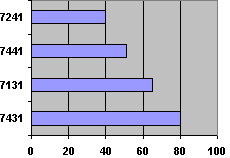 Рис. 3.11. Столбиковая диаграмма Рис. 3.12. Полосовая диаграмма Линейные, столбиковые и полосовые диаграммы имеют широкое применение в изображении статистической информации. При этом линейным и столбиковым диаграммам отдается предпочтение, если в изучаемых показателях проявляется общая тенденция роста. Горизонтальные полосы нагляднее, если изображаемые показатели отображают результат функционирования того или иного процесса. Для простого сравнения независимых друг от друга показателей могут использоваться диаграммы, принцип построения которых основан на том, что сравниваемые величины изображаются в виде правильных геометрических фигур (квадрат, круг, прямоугольник), площадь которых характеризует величину изучаемого признака. Эти диаграммы получили названия квадратных, круговых и знаков Варзара (рис.3.13-3.15). Для построения квадратных и круговых диаграмм необходимо из сравниваемых величин извлечь квадратный корень. Затем на основе полученных результатов определить сторону квадрата или радиус круга соответственно принятому масштабу. Квадраты или круги следует располагать на одинаковом друг от друга расстоянии. Также допускается построение таких диаграмм путем расположения один в другом квадратов или кругов и использования различной штриховки или закраски фигур. В каждой фигуре следует указывать числовое значение, которое она изображает, не приводя масштаба измерения. Для графического изображения статистических показателей применяются и так называемые знаки Варзара. В этих диаграммах используются прямоугольники для графического изображения тех показателей, один из которых является произведением двух других. В каждом таком прямоугольнике основание пропорционально одному из показателей-сомножителей, а высота его соответствует второму показателю-сомножителю. Площадь прямоугольника соответствует величине третьего показателя, являющегося произведением двух первых. Располагая рядом несколько прямоугольников, относящихся к разным показателям, можно сравнивать не только размеры показателя - произведения, но и значения показателей-сомножителей.
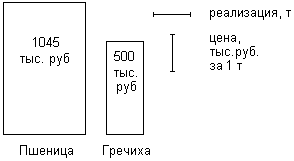 Рис. 3.15. Знаки Варзара В статистике, прежде всего для рекламных целей, применяются фигурные диаграммы. При их построении статистические данные изображаются рисунками, т.е. символами, которые в наибольшей степени соответствуют существу отображаемых явлений. Эти диаграммы более выразительны, зрительно легко воспринимаются. В фигурных диаграммах каждому знаку-символу условно придается определенное числовое значение, и путем последовательного их расположения на поле графика формируются соответствующие полосы. Величина отображаемого показателя определяется количеством стандартных знаков в каждой полосе (рис. 3.16). Недостатком фигурных диаграмм является то, что графическое изображение изучаемого явления знаками-символами не всегда соответствует точному значению изображаемых данных. Поэтому наряду с целыми фигурами приходится иметь дело с их частями. Это придает отображаемым показателям приближенное значение.
Для изображения на схематической географической карте статистических данных, характеризующих уровень или степень того или иного явления на определенной территории, используются статистические карты. Картограмма - это схематическая (контурная) карта или план местности, на которой отдельные территории в зависимости от величины изображаемого показателя обозначаются с помощью графических символов (штриховки, расцветки, точек). Картограммы подразделяются на фоновые и точечные (рис. 3.17, 3.18). В фоновых картограммах территории с различной величиной изучаемого показателя имеют различную штриховку. Иногда в качестве условных знаков используются различные цвета. При этом каждому значению показателя соответствует определенный оттенок раскраски или тип штриховки. Примером фоновых картограмм являются карты плотности населения, рождаемости, смертности. В точечных картограммах в качестве графического знака используются точки, размещенные в пределах определенных территориальных единиц. Каждая точка условно принимается за определенную величину показателя. Количественная характеристика отдельных территорий по размеру изучаемого показателя достигается при помощи соответствующего количества точек или их размера. Важное требование к точечным картограммам - выбор оптимального количественного значения точки. Если точки изображают слишком крупные числа, то создается впечатление оголенности территории. Если же взять точки со слишком малыми значениями, то они сливаются и не дают отчетливой картины. Точечные картограммы используются, например, для характеристики спроса и предложения товаров по отдельным регионам. Картодиаграммы представляют собой сочетание контурной карты местности с диаграммой. В отличие от диаграммы используемые геометрические символы (столбики, круги и др.) по картограммам располагают не в один ряд, а размещают по всей карте. Преимущество картодиаграммы перед диаграммой состоит в том, что она не только дает представление о величине изучаемого показателя, но и изображает пространственное размещение изучаемого показателя (рис. 3.19). 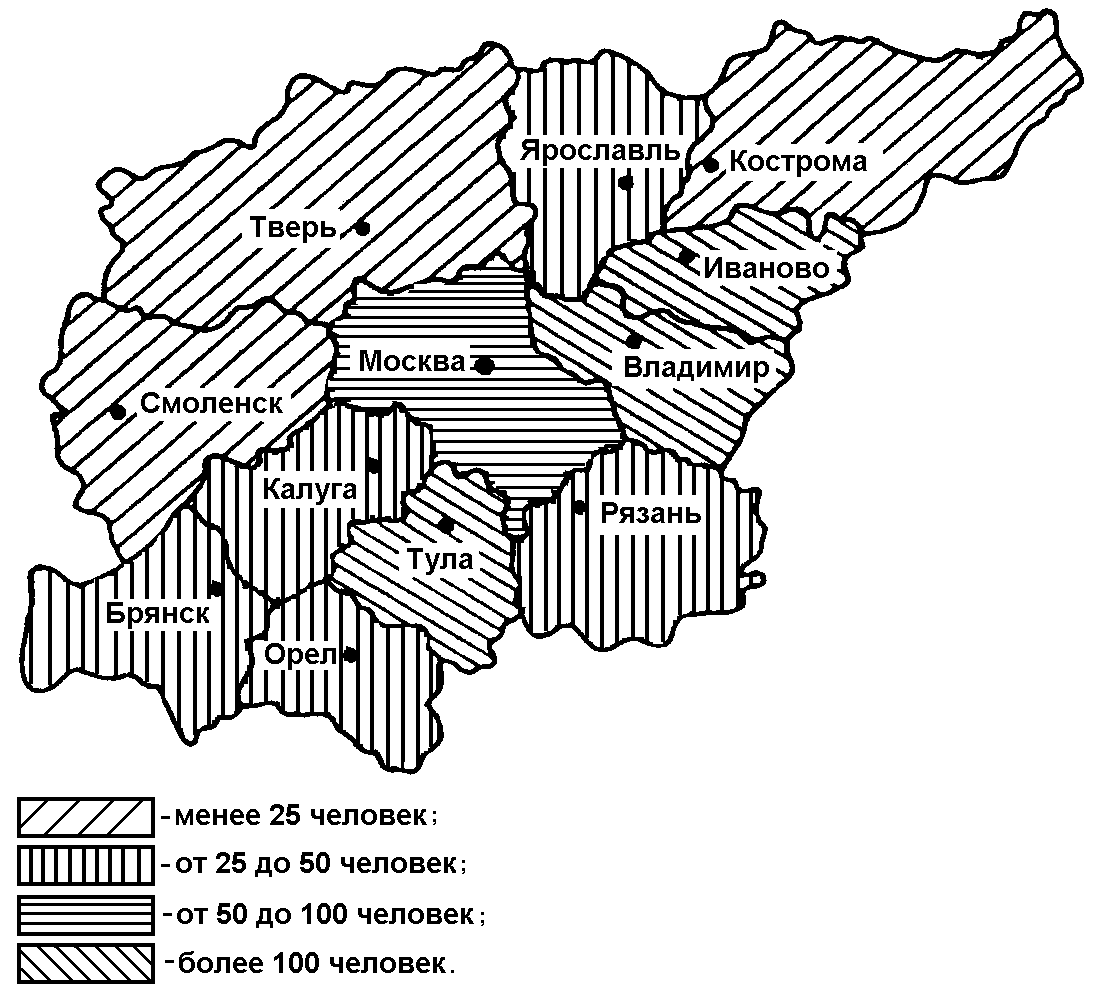 Рис. 3.17. Пример фоновой картограммы 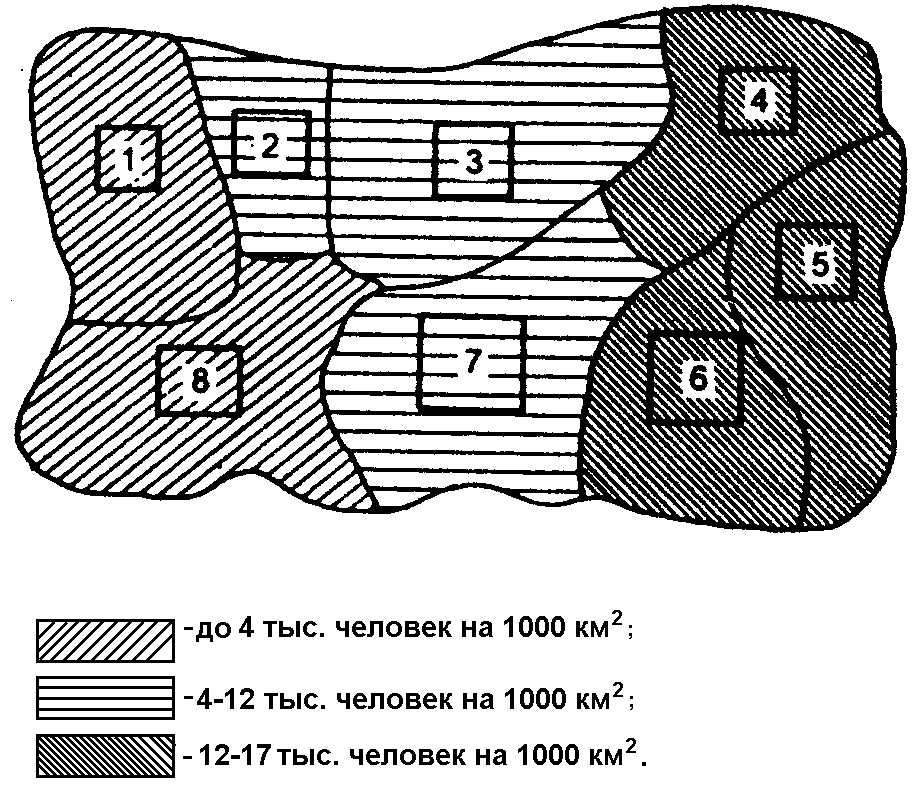 Рис. 3.18. Пример фоновой картограммы 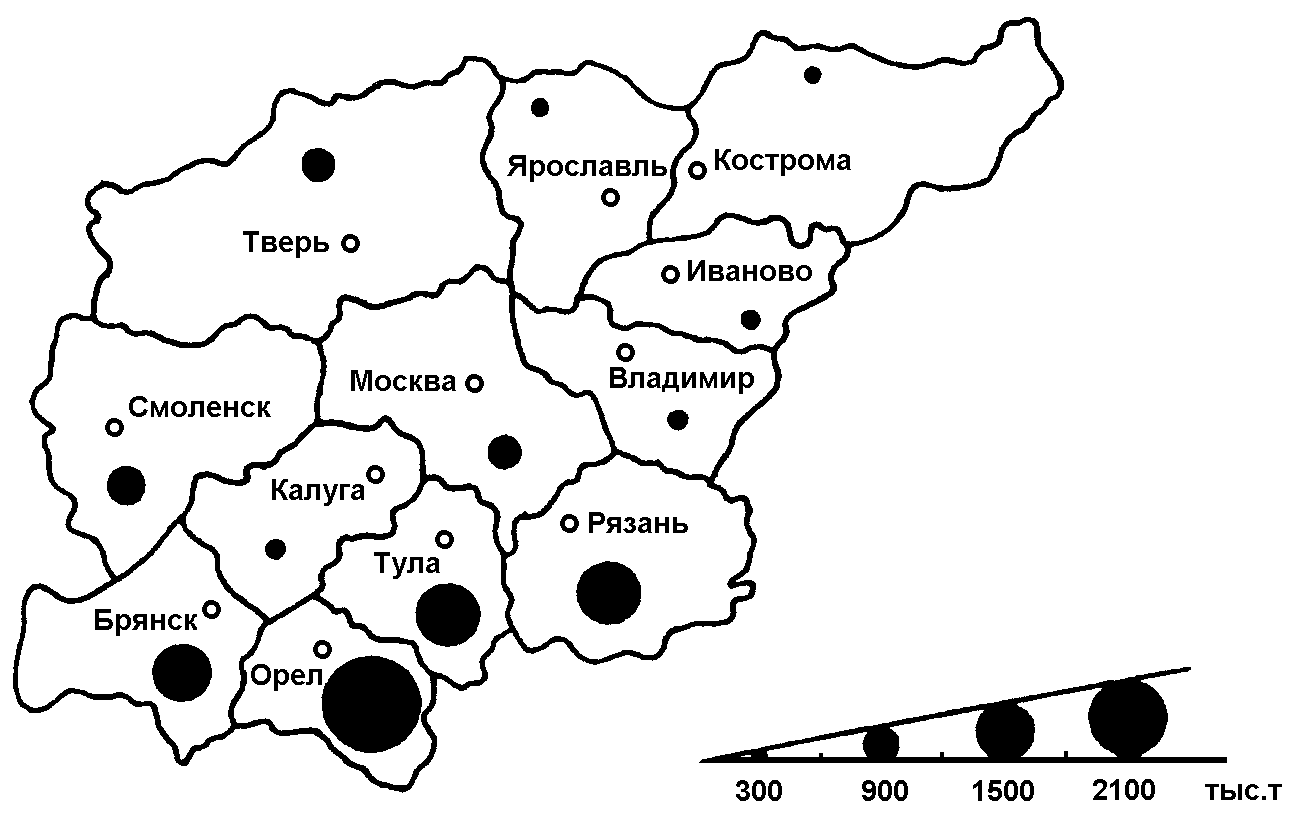 Рис. 3.19. Пример картодиаграммы Лекция 4. Абсолютные и относительные статистические величины 4.1. Понятие абсолютной и относительной величины в статистике Изучая массовые общественные явления, статистика в своих выводах опирается на числовые данные, полученные в конкретных условиях места и времени. Результаты статистического наблюдения регистрируются прежде всего в форме первичных абсолютных величин. Так, основная масса народнохозяйственных абсолютных показателей фиксируется в первичных учетных документах. Абсолютная величина отражает уровень развития явления. В статистике все абсолютные величины являются именованными, измеряются в конкретных единицах и, в отличие от математического понятия абсолютной величины, могут быть как положительными, так и отрицательными (убытки, убыль, потери и т.п.). Натуральные единицы измерения могут быть простыми (тонны, штуки, метры, литры) и сложными, являющимися комбинацией нескольких разноименных величин (грузооборот железнодорожного транспорта выражается в тонно-километрах, производство электроэнергии – в киловатт-часах). В статистике применяют и абсолютные показатели, выраженные в условно-натуральных единицах измерения (например, различные виды топлива пересчитываются в условное топливо). Стоимостные единицы измерения используются, например, для выражения объема разнородной продукции в стоимостной (денежной) форме – рублях. При использовании стоимостных измерителей принимают во внимание изменения цен с течением времени. Этот недостаток стоимостных измерителей преодолевают применением "неизменных" или "сопоставимых" цен одного и того же периода. В трудовых единицах измерения (человеко-днях, человеко-часах) учитываются общие затраты труда на предприятии, трудоемкость отдельных операций. С точки зрения конкретного исследования совокупность абсолютных величин можно рассматривать как состоящую из показателей индивидуальных, характеризующих размер признака у отдельных единиц совокупности, и суммарных, характеризующих итоговое значение признака по определенной части совокупности. Поскольку абсолютные показатели – это основа всех форм учета и приемов количественного анализа, то следует разграничивать моментные и интервальные абсолютные величины. Первые показывают фактическое наличие или уровень явления на определенный момент, дату (например, наличие запасов материалов или оборотных средств, величина незавершенного производства, численность проживающих и т.д.). Вторые – итоговый накопленный результат за период в целом (объем произведенной продукции за месяц или год, прирост населения за определенный период, величина валового сбора зерна за год и за пятилетку и т.п.). Сама по себе абсолютная величина не дает полного представления об изучаемом явлении, не показывает его структуру, соотношение между отдельными частями, развитие во времени. В ней не выявлены соотношения с другими абсолютными показателями. Эти функции выполняют определяемые на основе абсолютных величин относительные показатели. Относительная величина в статистике – это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных величин. Так как многие абсолютные величины взаимосвязаны, то и относительные величины одного типа в ряде случаев могут определяться через относительные величины другого типа. Основное условие правильного расчета относительной величины – сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями. Таким образом, по способу получения относительные показатели – всегда величины производные, определяемые в форме коэффициентов, процентов, промилле, продецимилле и т.п. Однако нужно помнить, что этим безразмерным по форме показателям может быть, в сущности, приписана конкретная, и иногда довольно сложная, единица измерения. Так, например, относительные показатели естественного движения населения, такие как коэффициенты рождаемости или смертности, исчисляемые в промилле (‰), показывают число родившихся или умерших за год в расчете на 1 000 человек среднегодовой численности; относительная величина эффективности использования рабочего времени – это количество продукции в расчете на один отработанный человеко-час и т.д. 4.2. Виды и взаимосвязи относительных величин Относительные величины образуют систему взаимосвязанных статистических показателей. По содержанию выражаемых количественных соотношений выделяют следующие типы относительных величин. 1. Относительная величина выполнения задания. Рассчитывается как отношение фактически достигнутого в данном периоде уровня к запланированному. Так, в 1988 г. было произведено стиральных машин 6103 тыс. шт. при плане (госзаказе) 6481 тыс. шт. Относительная величина выполнения плана составила Следовательно, плановое задание было недовыполнено на 5,8 %. На практике различают две разновидности относительных показателей выполнения плана. В первом случае сравниваются фактические и плановые уровни (таков пример, рассмотренный выше). Во втором случае в плановом задании устанавливается абсолютная величина прироста или снижения показателя и соответственно проверяется степень выполнения плана по этой величине. Так, если планировалось снизить себестоимость единицы продукции на 24,2 руб., а фактическое снижение составило 27,5 руб., то плановое задание по снижению себестоимости выполнено с ростом в 27,5 : 24,2 = 1,136 раза, т.е. план перевыполнен на 13,6 %. Показатель выполнения плана по уровню себестоимости в данном случае будет меньше единицы. Если фактическая себестоимость изделия равнялась 805,8 руб. при плановой 809,1 руб., то величина выполнения плана составила 805,8 : 809,1 = 0,996, или 99,6 %. Фактический уровень затратив одно изделие оказался на 0,4 % ниже планового. В аналитических расчетах при исследовании взаимосвязей чаще применяется оценка выполнения плана по уровню показателя. Оценка же выполнения плана по изменению уровня обычно приводится для целей иллюстрации, особенно если планируется снижение абсолютного значения затрат, расходов по видам и т.п. Относительные величины динамики, планового задания и выполнения плана связаны соотношением i=iпл.з.× iвып.пл. 2. Относительная величина динамики. Характеризует изменение уровня развития какого-либо явления во времени. Получается в результате деления уровня признака в определенный период или момент времени на уровень этого же показателя в предшествующий период или момент. 3. Относительные величины структуры. Характеризуют доли, удельные веса составных элементов в общем итоге. Как правило, их получают в форме процентного содержания:  Для аналитических расчетов предпочтительнее использовать коэффициентное представление, без умножения на 100. Совокупность относительных величин структуры показывает строение изучаемого явления. 5. Относительные величины координации (ОВК). Характеризуют отношение частей данной совокупности к одной из них, принятой за базу сравнения. ОВК показывают, во сколько раз одна часть совокупности больше другой либо сколько единиц одной части приходится на 1, 10, 100, 1000, ... единиц другой части. Относительные величины координации могут рассчитываться и по абсолютным показателям, и по показателям структуры. Так, приняв за базу сравнения поставки топливных ресурсов на экспорт в 1987 г., увидим, что на каждую условную тонну экспортных поставок приходится в 2,342 раза больше ресурсов, потребляемых внутри страны для производства энергии, и в 2,363 раза больше ресурсов, предназначенных для производственно-технологических целей. Уровень остатков на конец года составляет 57,8 % по сравнению с годовыми поставками на экспорт (9,20 : 15,91 = 242 : 418,3 = 0,578). По относительным величинам координации можно восстановить исходные относительные показатели структуры, если вычислить отношение относительной величины координации данной части (ОВК) к сумме всех ОВК (включая и ту, которая принята за базу сравнения): Например, доля экспортных поставок составляет 1 : (2,342 + 2,364 + 1 + 0,578) = 0,1591, или 15,9 %. 6. Относительные величины сравнения (ОВС). Характеризуют сравнительные размеры одноименных абсолютных величин, относящихся к одному и тому же периоду либо моменту времени, но к различным объектам или территориям. Посредством этих показателей сопоставляются мощности различных видов оборудования, производительность труда отдельных рабочих, производство продукции данного вида разными предприятиями, районами, странами. Например, по производству нефти и газа в 1985 г. СССР превосходил США: по нефти – в 1,36 раза, по газу – в 1,24 раза. Уровень производства электроэнергии (млрд. кВт • ч) в СССР составлял от уровня США 1544:2650 = 0,583, или 58,3 %. При известных коэффициентах роста (индексах динамики) и начальном соотношении уровней можно найти условие равенства уровней в предстоящем периоде t: Отсюда ОВСa / б =Ya / Yб=(ia / iб)t, т.е. Найденное значение t показывает, через какой период времени уровень изучаемого явления на объекте А сравняется с уровнем того же явления на объекте Б. Сопоставляя показатели динамики разных явлений, получают еще один вид относительных величин сравнения – коэффициенты опережения (отставания) по темпам роста или прироста. Так, если производительность труда на предприятии возросла на 12%, а фонд оплаты труда увеличился на 7,5 %, то коэффициент опережения производительности труда по темпам роста составит 112 : 107,5 = 1,042; коэффициент опережения по темпам прироста равен 12 : 7,5 = 1,60. 7. Относительные величины интенсивности. Характеризуют степень распределения или развития данного явления в той или иной среде. Представляют собой отношение абсолютного уровня одного показателя, свойственного изучаемой среде, к другому абсолютному показателю, также присущему данной среде и, как правило, являющемуся для первого показателя факторным признаком. Так, при изучении демографических процессов рассчитываются показатели рождаемости, смертности, естественного прироста и т.д. как отношение числа родившихся (умерших) или величины прироста населения за год к среднегодовой численности населения данной территории в расчете на 1000 чел. Если получаемые значения очень малы, то делают расчет на 10 000 человек. Относительными величинами интенсивности выступают, например, показатели выработки продукции в единицу рабочего времени, затрат на единицу продукции, трудоемкости, эффективности использования производственных фондов и т.д., поскольку их получают сопоставлением разноименных величин, относящихся к одному и тому же явлению и одинаковому периоду или моменту времени. Метод расчета относительных величин интенсивности применяется при определении средних уровней (среднего уровня выработки, средних затрат труда, средней себестоимости изделий, средней цены и т.д.). Поэтому распространено мнение, что относительные величины интенсивности – это один из способов выражения средних величин. Лекция 5. Средние величины. Показатели вариации 5.1. Понятие средней величины Средняя величина – это обобщающий показатель, характеризующий типический уровень явления. Он выражает величину признака, отнесенную к единице совокупности. Средняя всегда обобщает количественную вариацию признака, т.е. в средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами. В отличие от средней абсолютная величина, характеризующая уровень признака отдельной единицы совокупности, не позволяет сравнивать значения признака у единиц, относящихся к разным совокупностям. Так, если нужно сопоставить уровни оплаты труда работников на двух предприятиях, то нельзя сравнивать по данному признаку двух работников разных предприятий. Оплата труда выбранных для сравнения работников может быть не типичной для этих предприятий. Если же сравнивать размеры фондов оплаты труда на рассматриваемых предприятиях, то не учитывается численность работающих и, следовательно, нельзя определить, где уровень оплаты труда выше. В конечном итоге сравнить можно лишь средние показатели, т.е. сколько в среднем получает один работник на каждом предприятии. Таким образом, возникает необходимость расчета средней величины как обобщающей характеристики совокупности. Вычисление среднего – один из распространенных приемов обобщения; средний показатель выделяет то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей. Для того, чтобы средний показатель был действительно типизирующим, он должен рассчитываться с учетом определенных принципов. Остановимся на некоторых общих принципах применения средних величин. 1. Средняя должна определяться для совокупностей, состоящих из качественно однородных единиц. 2. Средняя должна исчисляться для совокупности, состоящей из достаточно большого числа единиц. 3. Средняя должна рассчитываться для совокупности, единицы которой находятся в нормальном, естественном состоянии. 4. Средняя должна вычисляться с учетом экономического содержания исследуемого показателя. 5.2. Виды средних и способы их вычисления Рассмотрим теперь виды средних величин, особенности их исчисления и области применения. Средние величины делятся на два больших класса: степенные средние, структурные средние. К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая. В качестве структурных средних рассматриваются мода и медиана. Остановимся на степенных средних. Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными. Простая средняя считается по не сгруппированным данным и имеет следующий общий вид: 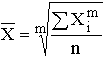 , ,где Xi – варианта (значение) осредняемого признака; m – показатель степени средней; n – число вариант. Взвешенная средняя считается по сгруппированным данным и имеет общий вид 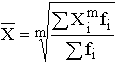 , ,где Xi – варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта; m – показатель степени средней; fi – частота, показывающая, сколько раз встречается i-e значение осредняемого признака. Приведем в качестве примера расчет среднего возраста студентов в группе из 20 человек:
Средний возраст рассчитаем по формуле простой средней: 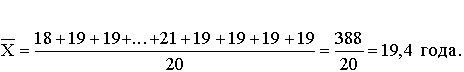 Сгруппируем исходные данные. Получим следующий ряд распределения:
В результате группировки получаем новый показатель – частоту, указывающую число студентов в возрасте Х лет. Следовательно, средний возраст студентов группы будет рассчитываться по формуле взвешенной средней: Общие формулы расчета степенных средних имеют показатель степени (m). В зависимости от того, какое значение он принимает, различают следующие виды степенных средних: средняя гармоническая, если m = -1; средняя геометрическая, если m –> 0; средняя арифметическая, если m = 1; средняя квадратическая, если m = 2; средняя кубическая, если m = 3. Формулы степенных средних приведены в табл. 4.4. Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина: В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные. Таблица 5.1 Виды степенных средних
Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т.е. m = Xf). К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т.д.) предприятиям, рабочим, занятым изготовлением одного и того же вида продукции, одной и той же детали, изделия. Главное требование к формуле расчета среднего значения заключается в том, чтобы все этапы расчета имели реальное содержательное обоснование; полученное среднее значение должно заменить индивидуальные значения признака у каждого объекта без нарушения связи индивидуальных и сводных показателей. Иначе говоря, средняя величина должна исчисляться так, чтобы при замене каждого индивидуального значения осредняемого показателя его средней величиной оставался без изменения некоторый итоговый сводный показатель, связанный тем или другим образом с осредняемым. Этот итоговый показатель называется определяющим, поскольку характер его взаимосвязи с индивидуальными значениями определяет конкретную формулу расчета средней величины. Покажем это правило на примере средней геометрической. Формула средней геометрической 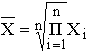 используется чаще всего при расчете среднего значения по индивидуальным относительным величинам динамики. Средняя геометрическая применяется, если задана последовательность цепных относительных величин динамики, указывающих, например, на рост объема производства по сравнению с уровнем предыдущего года: i1, i2, i3,..., in. Очевидно, что объем производства в последнем году определяется начальным его уровнем (q0) и последующим наращиванием по годам: qn=q0× i1× i2×...×in. Приняв qn в качестве определяющего показателя и заменяя индивидуальные значения показателей динамики средними, приходим к соотношению 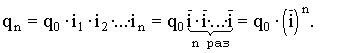 Отсюда 5.3. Структурные средние Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен (например, если бы в рассмотренном примере отсутствовали данные и об объеме производства, и о сумме затрат по группам предприятий). В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. Модой ( 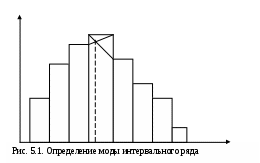 ода широко используется в коммерческой практике при изучении покупательского спроса, например, при определении размеров одежды и обуви, которые пользуются наибольшим спросом. ода широко используется в коммерческой практике при изучении покупательского спроса, например, при определении размеров одежды и обуви, которые пользуются наибольшим спросом.В интервальном ряду модой приближенно считают центральное значение так называемого модального интервала, т.е. того интервала, который имеет наибольшую частоту. В пределах интервала надо найти то значение признака, которое является модой (рис. 5.1). Для интервального ряда распределения расчет моды производится по специальной формуле: где Недостатком моды является то, что ее значение может быть определено неоднозначно: максимум Поэтому мода обычно определяется для дискретных признаков или для интервальных рядов. Распределение признака часто бывает унимодальным, поэтому в большинстве случаев мода определяется однозначно. Введем теперь следующий показатель - медиану. Пусть объекты в статистической совокупности упорядочены по возрастанию значений признака, т.е. Медиана ( Для ранжированного ряда с четным числом членов В 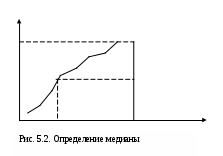 интервальном ряду порядок нахождения медианы следующий: определяем для данного ряда накопленные частоты. Медиана попадает в тот интервал, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая накопленная частота меньше половины численности совокупности (рис. 5.2). интервальном ряду порядок нахождения медианы следующий: определяем для данного ряда накопленные частоты. Медиана попадает в тот интервал, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая накопленная частота меньше половины численности совокупности (рис. 5.2).Error: Reference source not found Медиана в интервальном ряду распределения вычисляется по формуле 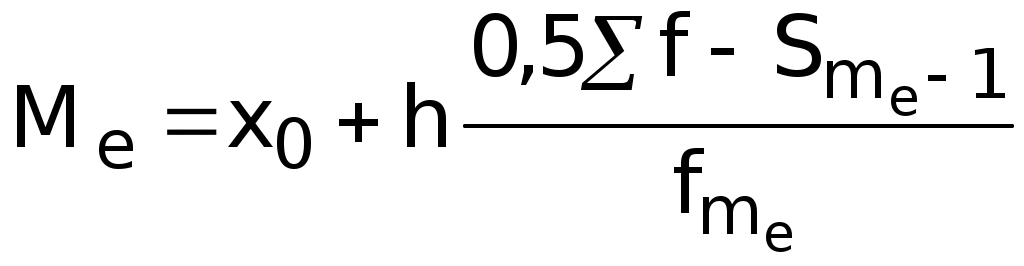 , ,где Медиана более определена, чем мода и ее основное практическое применение связано с тем, что сумма абсолютного отклонения членов ряда от медианы есть величина наименьшая: Отметим, что структурные средние не связаны с определяющим показателем. Они не основные, а дополнительные характеристики совокупности. Помимо моды и медианы, можно определить и другие структурные характеристики статистической совокупности (рис. 5.3). Например, пусть Error: Reference source not found 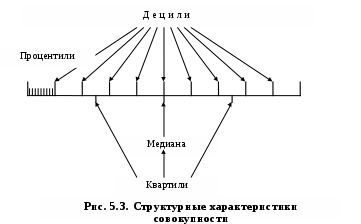 5.4. Показатели вариации Конкретные условия, в которых находится каждый из изучаемых объектов, а также особенности их собственного развития (социальные, экономические и пр.) выражаются соответствующими числовыми уровнями статистических показателей. Таким образом, вариация, т.е. несовпадение уровней одного и того же показателя у разных объектов, имеет объективный характер и помогает познать сущность изучаемого явления. Для измерения вариации в статистике применяют несколько способов. Наиболее простым является расчет показателя размаха вариации R как разницы между максимальным (Xmax ) и минимальным (Xmin) наблюдаемыми значениями признака: R=Xmax - Xmin. Однако размах вариации показывает лишь крайние значения признака. Повторяемость промежуточных значений здесь не учитывается. Более строгими характеристиками являются показатели колеблемости относительно среднего уровня признака. Простейший показатель такого типа – среднее линейное отклонение Л как среднее арифметическое значение абсолютных отклонений признака от его среднего уровня: При повторяемости отдельных значений Х используют формулу средней арифметической взвешенной: (Напомним, что алгебраическая сумма отклонений от среднего уровня равна нулю.) Показатель среднего линейного отклонения нашел широкое применение на практике. С его помощью анализируются, например, состав работающих, ритмичность производства, равномерность поставок материалов, разрабатываются системы материального стимулирования. Но, к сожалению, этот показатель усложняет расчеты вероятностного типа, затрудняет применение методов математической статистики. Поэтому в статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии. Дисперсия признака ( 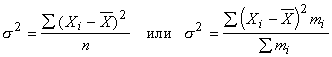 . .Показатель В общей теории статистики показатель дисперсии является оценкой одноименного показателя теории вероятностей и (как сумма квадратов отклонений) оценкой дисперсии в математической статистике, что позволяет использовать положения этих теоретических дисциплин для анализа социально-экономических процессов. Если вариация оценивается по небольшому числу наблюдений, взятых из неограниченной генеральной совокупности, то и среднее значение признака определяется с некоторой погрешностью. Расчетная величина дисперсии оказывается смещенной в сторону уменьшения. Для получения несмещенной оценки выборочную дисперсию, полученную по приведенным ранее формулам, надо умножить на величину n / (n - 1). В итоге при малом числе наблюдений (< 30) дисперсию признака рекомендуется вычислять по формуле 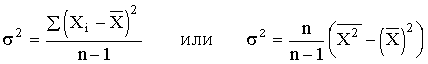 . .Обычно уже при n > (15÷20) расхождение смещенной и несмещенной оценок становится несущественным. По этой же причине обычно не учитывают смещенность и в формуле сложения дисперсий. Если из генеральной совокупности сделать несколько выборок и каждый раз при этом определять среднее значение признака, то возникает задача оценки колеблемости средних. Оценить дисперсию среднего значения можно и на основе всего одного выборочного наблюдения по формуле где n – объем выборки; Величина Показатели относительного рассеивания. Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%. 1. Коэффициентом осцилляции отражают относительную колеблемость крайних значений признака вокруг средней 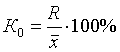 . .2. Относительное линейное отклонение характеризует долю усредненного значения признака абсолютных отклонений от средней величины 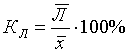 . .3. Коэффициент вариации: 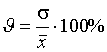 является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин. Коэффициент является наиболее значимым при оценке однородности изучаемой совокупности. Чем он больше, тем неоднороднее группа. В качестве критерия однородности исследуемой совокупности принято значение показателя вариации 33% (для нормального распределения). Если изучаемая совокупность имеет показатель вариации 33%, то она считается однородной. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||