Линейные и нелинейные системы. Описание и примеры
 Скачать 1.16 Mb. Скачать 1.16 Mb.
|
|
Виды m-файлов. Создание, вызов, отладка m-файлов М-файлы представляют собой обыкновенные текстовые файлы, содержащие команды программы MATLAB. М-файлы позволяют сохранять множество команд программы MATLAB в одном файле, а затем запускать их одной командой или с использованием мыши.M-файлы бывают 2х видов: М-файлы-сценарии и М-файлы-функиии. Сценарии являются самым простым типом M-файла – у них нет входных и выходных аргументов. Они используются для автоматизации многократно выполняемых вычислений. Сценарии оперируют данными из рабочей области и могут генерировать новые данные для последующей обработки в этом же файле. Данные, которые используются в сценарии, сохраняются в рабочей области после завершения сценария и могут быть использованы для дальнейших вычислений. Сценарий производит вычисления как с переменными, которые определяются непосредственно внутри него, так и с переменными, ранее определёнными в рабочем пространстве системы MATLAB. Таким образом, пространство переменных у них общее. М-функции являются M-файлами, которые допускают наличие входных и выходных аргументов. Они работают с переменными в пределах собственной рабочей области, отличной от рабочей области системы MATLAB. Если функция имеет более одного выходного аргумента, список выходных аргументов помещается в квадратные скобки. Входные аргументы, если они присутствуют, помещаются в круглые скобки. Для отделения аргументов во входном и выходном списках применяются запятые. Пример function [x, y, z] = sphere(theta, phi, rho) Имена входных переменных могут, но не обязаны совпадать с именами, указанными в строке определения функции. ОТЛАДКА М-файлов. Для подготовки, редактирования и отладки m-файлов служит специальный многооконный редактор. Редактор можно вызвать командой edit из командной строки или командой New > M-file из меню File. После этого в окне редактора можно создавать свой файл, пользоваться средствами его отладки и запуска. Перед запуском файла его необходимо записать на диск, используя команду Filе > Save as в меню редактора. Запустив команду Run, можно наблюдать исполнение m-файла; на деле редактор/отладчик выполняет важную роль. Он позволяет создать m-файл (программу) без той многочисленной «шелухи», которая сопровождает работу в командном режиме. Далее мы убедимся, что текст такого файла подвергается тщательной синтаксической проверке, в ходе которой выявляются и отсеиваются многие ошибки пользователя. Таким образом, редактор обеспечивает синтаксический контроль файла. Редактор имеет и другие важные отладочные средства — он позволяет устанавливать в тексте файла специальные метки, именуемые точками прерывания (breakpoints). При их достижении вычисления приостанавливаются, и пользователь может оценить промежуточные результаты вычислений (например, значения переменных), проверить правильность выполнения циклов и т. д. Наконец, редактор позволяет записать файл в текстовом формате и увековечить ваши труды в файловой системе MATLAB. Нули и полюсы функции передачи. Коэффициент усиления функции передачи. Нулями называются корни числителя, полюсами – корни знаменателя. По передаточной функции можно легко построить модель в форме «нули-полюса» f_zpk = zpk(w) Одна из важнейших характеристик линейной системы – коэффициент усиления в установившемся режиме или статический коэффициент усилении (staticgain, DC-gain). Его можно определить как установившееся значение сигнала выхода при постоянном входном сигнале, равном единице. Размерность этой величины равна отношению размерностей сигналов выхода и выхода. Чтобы найти статический коэффициент усиления модели f в Matlab, используется команда k = dcgain ( f ) Для нахождения полюсов передаточной функции f можно использовать функцию p = pole ( f ) Вызов функции [w0,zeta,p] = damp ( f ) позволяет найти не только полюса p, но также соответствующие им собственные частоты w0 и коэффициенты демпфирования zeta в виде массивов. Нули передаточной функции f вычисляются как z = zero ( f ); Устойчивость системы не зависит от расположения нулей, но они существенно влияют на переходные процессы. Команда pzmap ( f ); строит карту расположения нулей (они обозначаются кружками) и полюсов (крестики) системы на комплексной плоскости. 21. Виды звеньев. Передаточные функции звеньев. Звеном системы называется ее элемент (часть), обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь самую разнообразную физическую основу (электрические, гидравлические, механические и т. п.) и конструктивное выполнение, но при этом относиться к одной функциональной группе. Соотношение входного и выходного сигналов в звеньях одной и той же группы описывается одинаковыми дифференциальными уравнениями. Это свидетельствует о том, что такие звенья имеют одинаковые динамические свойства. Так как процесс автоматического регулирования определяется только динамическими свойствами системы (а следовательно, и ее звеньев), то в основу классификации звеньев положены их динамические свойства. Такая классификация звеньев по виду описывающих эти звенья дифференциальных уравнений дает возможность разработать стройную теорию АСР и единые методы их исследования и расчета, не зависящие от различий в физических процессах и конструктивных решениях, принятых в основу при проектировании АСР и ее элементов. Простейшими типовыми звеньями АСР являются: усилительное, интегрирующее, апериодическое, колебательное, дифференцирующее, запаздывающее. Безынерционным звеном (усилительным, идеальным, пропорциональным, безъемкостным, первого порядка и т.п.) называется такое звено, передача сигнала от входа к выходу которого осуществляется мгновенно, без какой-либо инерции. Для безынерционного звена статическая характеристика совпадает с динамической характеристикой. Примерами такого звена являются рычаг, потенциометр, трансформатор, механическая передача. Интегрирующим или астатическим называется такое звено, в котором выходная величина пропорциональна по времени интегралу от входной величины. Инерционным звеном или апериодическим называется звено, в котором при подаче на вход скачкообразного сигнала его выходная величина запаздывает относительно входной и изменяется апериодически по экспоненциальной кривой с постоянной времени  по уравнению. по уравнению. Колебательным называется звено, в котором при скачкообразном изменении величины на входе выходная величина стремится к новому установившемуся значению, совершая относительно него колебания с амплитудой, затухающей по закону экспоненты. 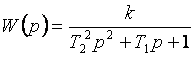 . . .Дифференцирующим звеном называется такое звено, в котором в идеальном случае выходная величина является производной от входной величины.Примерами такого звена являются тахогенератор, демпфер в механических передачах, электрические контуры, включающие активные и индуктивные сопротивления и др Выходная величина в запаздывающем звене точно повторяет входную величину, но с некоторым запаздыванием по времени Использование глобальных переменных в MATLAB. При использовании нескольких функций бывает необходимо, чтобы им была доступна одна переменная для ее модификации. Глобальные переменные объявляются в каждом файле. Команда: global имя1 имя2 . . . определяет переменные с именами имя1, имя2, . . . как "глобальные" . Если несколько функций и сценарий объявляют некоторую переменную глобальной, то все они используют одну и ту же копию этой переменной. Изменение ее значения в одной из функций приведет к тому, что при последующем обращении ко всем остальным функциям указанная переменная принимает измененное значение. Это же измененное значение принимает переменная с этим именем в рабочей области (та которую можно посмотреть в командном окне). 23. Оператор цикла с предварительным условием и цикл с параметром.  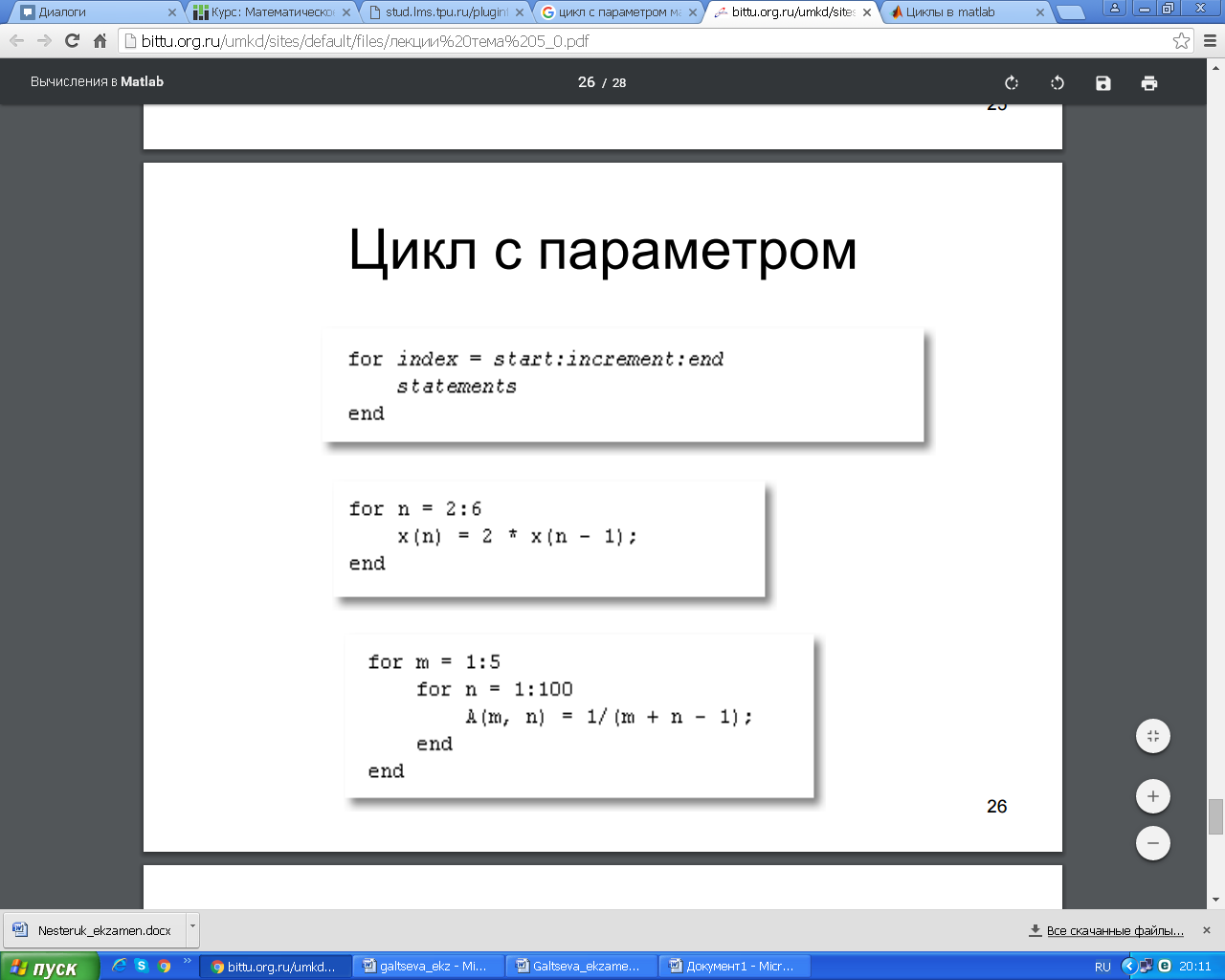 Часто при организации цикла требуется перебирать значение счетчика в заданном диапазоне значений и с заданным шагом изменения. Например, чтобы перебрать элементы вектора (массива), нужно организовать счетчик от 1 до N с шагом 1, где N – число элементов вектора. Чтобы вычислить сумму ряда, также задается счетчик от a до b с требуемым шагом изменения step. И так далее. В связи с тем, что подобные задачи часто встречаются в практике программирования, для их реализации был предложен свой оператор цикла for, который позволяет проще и нагляднее реализовывать цикл со счетчиком. Синтаксис оператора цикла for имеет следующий вид: for <счетчик> = <начальное значение>:<шаг>:<конечное значение> <операторы цикла> end  Здесь <условие> означает условное выражение подобное тому, которое применяется в операторе if, и цикл while работает до тех пор, пока это условие истинно. Следует обратить внимание на то, что если условие будет ложным до начала выполнения цикла, то операторы, входящие в цикл, не будут выполнены ни разу. 24.Форматный вывод данных в m-файле. Форматный вывод данных позволяет управлять шириной полей вывода, количество значащих цифр в числовых данных, а также отступами, пробелами, табуляцией переводами строк и другими параметрами представления – т.е. форматом данных при их выводе. Функция fprintf() позволяет выводить информацию на экран и имеет вид: fprintf (идентификатор файла, 'форматы', список переменных) В списке переменных могут быть как числовые переменные (или числа), так и строковые переменные (или строки). Второй аргумент является строкой специального вида с форматами, в которых будут выводиться все элементы из списка. Каждый формат начинается со знака процента. Для вывода строк используется формат s, а для вывода чисел — f (с плавающей точкой) или e (экспоненциальный). Число перед s указывает количество позиций, отводимых под вывод строки. При выводе значений числовых переменных перед f или e ставится два числа, разделенных точкой. Первое из них означает количество позиций, выделяемых под все значение переменной, а второе — количество знаков после десятичной точки. Таким образом, под каждый из элементов списка отводится поле определенной длины, выравнивание в котором по умолчанию производится по правому краю. Для выравнивания по левому краю следует после знака процента поставить знак минус. Ниже приведены варианты вызова fprintf и результаты, незаполненные позиции после вывода (пробелы) обозначены символом ○  Ниже перечислены основные виды спецификаторов: %с – одиночный символ %d – десятичное целое число со знаком %f – число с плавающей точкой (десятичное представление) %s – строка символов (для строковых переменных) %u – десятичное целое без знака %% - печать знака процента 25. Модуль LTIViewer в программе MATLAB. Инструмент Simulink LTI-Viewer входит в состав пакета прикладных программ Control System Toolbox и предназначен для анализа линейных стационарных систем. С помощью данного инструмента можно легко построить частотные характеристики исследуемой системы, получить ее отклики на единичные ступенчатое и импульсное воздействия, найти нули и полюса системы и т.д. Краткий алгоритм работы с Simulink LTI-Viewer приведен ниже. Работа с Simulink LTI-Viewer 1. Выполнить команду Tools\LinearAnalysis... окна Simulink-модели. В результате выполнения команды откроется окно Model_Inputs_and_Outputs, а также пустое окно Simulink LTI-Viewer . 2. Установить блок Input Point на входе и блок Output Point на выходе исследуемой системы. 3. Вокне LTI Viewer выполнитькоманду Simulink\Get Linearized Model. Данная команда выполняет линеаризацию модели и строит реакцию системы на единичное ступенчатое воздействие. Если система имеет несколько входов и выходов и для всех них установлены блоки Input Point и Output Point, то на графике будет отображено несколько окон показывающих реакцию на каждом выходе при воздействии на каждый вход. 4. Для получения остальных характеристик системы необходимо выполнить команду Edit\Plot Configuration... в окне LTI Viewer. В результате выполнения этой команды откроется окно Plot Configuration. В открывшемся окне можно выбрать число отображаемых графиков (панель Select a response plot configuration) и вид отображаемых графиков (панель Response type). Для построения доступны следующие графики (диаграммы): step – Реакция на единичное ступенчатое воздействие. impulse – Реакция на единичное импульсное воздействие. bode – Логарифмические амплитудная и фазовая частотные характеристики. bode mag – Логарифмическая амплитудная частотная характеристика. nyquist – Диаграмма Найквиста. nichols – Годограф Николса. sigma – Сингулярные числа. pole/zero – Нули и полюса системы. Настройку внешнего вида графиков можно выполнить с помощью команды Edit\Line Styles…(установка вида и цвета линий, вида маркеров). Настройка Simulink LTI-Viewer С помощью команды Edit\Viewer Preferences… выполняются следующие виды настройки: 1. Установка единиц измерения (вкладка Units). Вкладка Units окна позволяет задать единицы измерения частоты (рад/c или Гц), уровня (dB или абсолютные единицы), фазы (градусы или радианы), а также установить вид шкалы частоты (логарифмический или линейный). 2. Установка стиля графиков (вкладка Style). На данной вкладке можно выполнить настройку шрифтов окна Simulink LTI-Viewer (панель Fonts), выбрать цвет осей графиков (панель Colors), а также задать нанесение линий сетки на графики (флажок Show grids). 3. Установка параметров расчета переходного процесса (вкладка Characteristics). Данная вкладка позволяет задать параметры установленные "по умолчанию" для вычисления времени нарастания и времени переходного процесса. По умолчанию Simulink LTI-Viewer вычисляет время переходного процесса как время, когда переходная функция входит в 2% зону и больше не выходит из нее (параметр Show setting time within). Также можно изменить параметры для вычисления времени переходного процесса (Show rise time from). На данной вкладке имеется также флажок Unwrap phase, установка которого позволяет избежать отображения разрывов в фазо-частотной характеристике, связанных с областью определения функции arctg, вычисляющей фазовый сдвиг. 4. Установка интервалов времени и частоты (вкладка Parameters). На данной вкладке задается временной интервал для расчета переходного процесса (панель Time Vector), а также интервал частот для расчета частотных характеристик (панель Frequency Vector). Векторы времени и частоты можно вычислять в автоматическом режиме (Generate automatically), ввести конкретное значение для времени окончания расчета (Define stop time) или диапазон значений по частоте (Define range), либо задать непосредственно вектор значений времени или частоты (Define vector). 26. Алгебраические и частотные критерии устойчивости. Критерии устойчивости представляют собой правила, устанавливающие устойчивость системы и выявляющие влияние тех или иных параметров и структурных изменений в системе на устойчивость. Критерии-устойчивости можно разделить на алгебраические и частотные. Алгебраические критерии позволяют определять устойчивость путем выполнения алгебраических операций над коэффициентами исходного дифференциального уравнения системы, не прибегая к графическим построениям. Частотные критерии устойчивости имеют более явный физический смысл. Они позволяют сравнительно просто оценить устойчивость системы и влияние параметров отдельных ее элементов на устойчивость. Частотные критерии устойчивости, основанные на использовании частотных характеристик, относятся к графоаналитическим, т. к. устойчивость оценивают по виду годографа частотой характеристики. Достоинством этого метода является его наглядность и возможность экспериментального определения частотных характеристик как отдельных звеньев, так и системы в целом. Алгебраические критерии Рауса и Гурвица устанавливают условие устойчивости на базе определенных комбинаций, составленных из коэффициентов характеристических уравнений вида 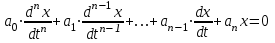 и и 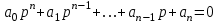 . .Критерий Рауса. Для определения устойчивости линейной АСР по критерию Рауса составляется таблица Рауса. Коэффициенты таблицы называются элементами Рауса. Обозначают каждый элемент через bre , где r – номер строки таблицы Рауса: е — номер столбца. Тогда правила заполнения таблицы Рауса сводятся к следующему. Элементами первой строки таблицы Рауса являются коэффициенты характеристического уравнения с четными индексами, т. е. b11=a0, b12=a2b и т.д. Элементами второй строки таблицы Рауса являются коэффициенты характеристического уравнения с нечетными индексами, т. е b21=a1, b22=a3 . Элементы остальных строк таблицы определяются на основании общего выражения  . .Критерий Рауса, исходя из принципа левых корней характеристического уравнения, устанавливает следующее условие устойчивости: линейная АСР будет устойчива, если все элементы первого столбца таблицы Рауса положительны, т. е. b11>0, b21>0; br1>0. Критерий Гурвица. Для определения устойчивости АСР по критерию Гурвица характеристическое уравнение также приводится к виду ( 2 ). Далее из коэффициентов характеристического уравнения составляются определители Гурвица по форме  , ,  , , , где n — порядок уравнения АСР. , где n — порядок уравнения АСР.Общее правило составления определителей Гурвица сводится к следующему: число строк и столбцов определителя 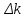 равно k; по диагонали определителя располагаются коэффициенты характеристического уравнения от а1_ до ak; слева от диагонали на каждой строке располагаются коэффициенты с возрастающими индексами, вправо—с убывающими, причем правее a0 пишутся нули; все коэффициенты с индексами, значения которых превышают степень характеристического уравнения, заменяются нулями. Характеристическое уравнение перед составлением определителей Гурвица должно быть приведено к такому виду, при котором a0>0. равно k; по диагонали определителя располагаются коэффициенты характеристического уравнения от а1_ до ak; слева от диагонали на каждой строке располагаются коэффициенты с возрастающими индексами, вправо—с убывающими, причем правее a0 пишутся нули; все коэффициенты с индексами, значения которых превышают степень характеристического уравнения, заменяются нулями. Характеристическое уравнение перед составлением определителей Гурвица должно быть приведено к такому виду, при котором a0>0.Критерий устойчивости Гурвица сводится к следующему: линейная АСР будет устойчива, если все коэффициенты характеристического уравнения и все п определителей Гурвица положительны. Условия устойчивости АСР невысокого порядка определяются простыми соотношениями коэффициентов характеристического уравнения, вытекающими из критериев Рауса и Гурвица. В частности, для систем 1-го и 2-го порядка признаком устойчивости является положительность всех коэффициентов характеристического Структура определителей Гурвица показывает, что последний определитель n АСР равен 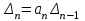 , а уравнением границы устойчивости АСР является , а уравнением границы устойчивости АСР является 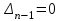 Критерий Найквиста - частотный критерий, позволяющий по виду амплитудно-фазовой частотной характеристики разомкнутой системы оценить устойчивость работы замкнутой системы. АФЧХ может быть получена экспериментально или аналитически. Аналитическое построение АФЧХ производится обычными методами. Критерий Найквиста формулируется по разному в зависимости от того, устойчива разомкнутая система или нет. Если разомкнутая система устойчивая, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до ∞ не охватывала точку с координатами -i, j0. Если АФЧХ разомкнутой системы проходит через точку с координатами -i, j0, то система будет нейтральной. На рис представлены АФЧХ разомкнутых статических систем. Критерий Найквиста позволяет наглядно проследить влияние изменения параметров передаточной функции на устойчивость системы. 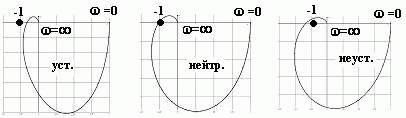 Рис АФЧХ разомкнутых САУ По ЛЧХ разомкнутой системы можно определить запасы устойчивости: запас по фазе φзап отсчитывается по л.ф.х. на частоте среза ωср и равен φзап=π - φ(ωср), а запас по амплитуде Lзап соответствует значению л.а.х. на частоте, при которой л.ф.х. равна -π (рис.4.7). Если φ(ωср)=-&pi, то система находится на границе устойчивости. Критический коэффициент усиления разомкнутой системы Kкр определяется из выражения 20*lg(Kкр)=20*lg(Kраз) + Lзап. Критерий Михайлова формулируется так: система устойчива, если годограф Михайлова M(jω) при изменении от 0 до +∞ , начинаясь на положительной части действительной оси, обходил последовательно в положительном направлении (против часовой стрелки) n квадрантов и в n-м квадранте уходил в ∞. Если годограф начинается в нулевой точке комплексной плоскости или проходит через эту точку при определенной частоте, то система считается нейтральной. В этом случае P(ω) = 0 и Q(ω) = 0. Из этих уравнений можно определить значения параметров, при которых система находится на границе устойчивости (критические значения). На рис.4.3 приведены годографы Михайлова для устойчивых и неустойчивых САУ.  |
