Линейные и нелинейные системы. Описание и примеры
 Скачать 1.16 Mb.
|
|
Структуры данных в MATLAB. Структурыотносятся к сложным типам данных. Структуры могут содержать разнородные данные, относящиеся к некоторому именованному объекту. Например, объект man (человек) может характеризоваться следующими данными:
Первые два столбца представляют схему структуры.Как нетрудно заметить, каждая i-яструктура состоит из ряда полей,имеющих имена,например man(i).name, man(i) .date и т. д. Поля могут содержать данныелюбого типа — от пустого поля [ ] до массивов. Приведенная выше структура имеет размер 1x1. MATLAB поддерживает и массивы структур, что позволяет создавать мощные базы данных. Поле структуры может содержать другую вложенную структуру или массив структур. Это позволяет создавать вложенные структуры и даже многомерные массивы структур. Описание линейных систем с помощью пространства состояний (параметры A, В, С, D). Пространство состояний — в теории управления один из основных методов описания поведения динамической системы. Движение системы в пространстве состояний отражает изменение ее состояний. В пространстве состояний создаётся модель динамической системы, включающая набор переменных входа, выхода и состояния, связанных между собой дифференциальными уравнениями первого порядка, которые записываются в матричной форме. В отличие от описания в виде передаточной функции и других методов частотной области, пространство состояний позволяет работать не только с линейными системами и нулевыми начальными условиями. 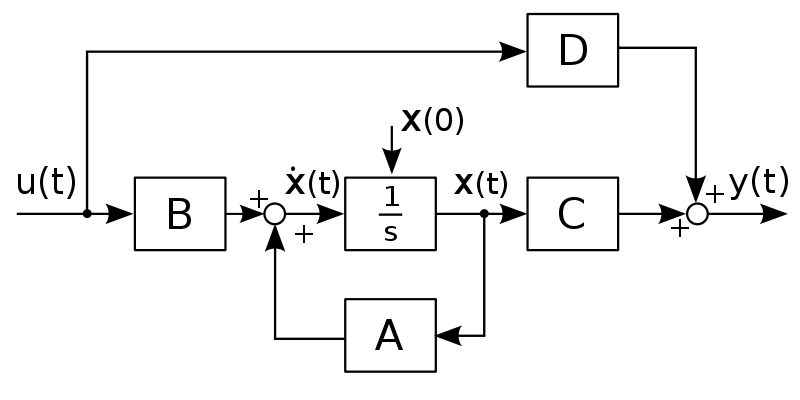 Еще одним способом описания линейной цепи является ее представление в пространстве состояний. При этом состояние цепи описывается вектором состояния x(t), а собственные колебания цепи и ее реакция на входной сигнал u(t) характеризуются следующим образом:x’(t)=Ax(t)+Bu(t), (1) y(t)=Cx(t)+Du(t).  — вектор состояния, элементы которого называются состояниями системы — вектор выхода, — вектор управления, — матрица системы, — матрица управления, — матрица выхода, — матрица прямой связи.Что такое функция Дирака? Единичная функция Единичный импульс или дельта-функция Дирака 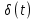 . Это идеальный (невозможный в реальной жизни) сигнал, который равен нулю во всех точках, кроме t = 0, где он уходит к бесконечность, причем его площадь (интеграл по всей оси времени) равен единице: 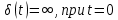 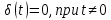 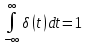 Поскольку бесконечный импульс невозможно нарисовать, на графике он изображается стрелкой, высота которой равна единице. 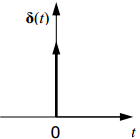  Реакция системы на единичный импульс (дельта-функцию) называется импульсной ха- рактеристикой и обозначается w(t): 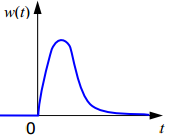 Используется как прямоугольный сигнал единичной площади Единичная функция: 1(t) . 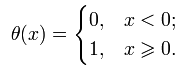 При действии на вход единичного ступенчатого сигнала 1(t) (или дельта-функции ) δ(t) на выходе будет такой же сигнал, усиленный в k раз. Функция Хевисайда (единичная ступенчатая функция, функция единичного скачка, включенная единица) — кусочно-постоянная функция, равная нулю для отрицательных значений аргумента и единице — для положительных. В нуле эта функция, вообще говоря, не определена, однако её обычно доопределяют в этой точке некоторым числом, чтобы область определения функции содержала все точки действительной оси. Чаще всего неважно, какое значение функция принимает в нуле, поэтому могут использоваться различные определения функции Хевисайда, удобные по тем или иным соображениям. Аналоговые, дискретные и цифровые сигналы. Исходный физический сигнал является непрерывной функцией времени. Такие сигналы, определенные во все моменты времени, называют аналоговыми (analog). Последовательность чисел, представляющая сигнал при цифровой обработке, является дискретным рядом (discrete series) и не может полностью соответствовать аналоговому сигналу. Числа, составляющие последовательность, являются значениями сигнала в отдельные (дискретные) моменты времени и называются отсчетами сигнала (samples). Как правило, отсчеты берутся через равные промежутки времени Т, называемые периодом дискретизации (или интервалом, шагом дискретизации - sample time). Величина, обратная периоду дискретизации, называется частотой дискретизации (sampling frequency): 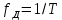 . Соответствующая ей круговая частота определяется следующим образом: 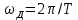 .Сигнал, дискретный во времени, но не квантованный по уровню, называется дискретным (discrete-time) сигналом. Сигнал, дискретный во времени и квантованный по уровню, называют цифровым (digital) сигналом. Сигналы, квантованные по уровню, но непрерывные во времени, на практике встречаются редко. Разницу между аналоговыми, дискретными к цифровыми сигналами иллюстрирует рис. 3.1.  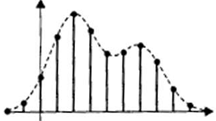 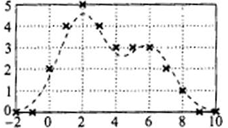 Частота Найквиста. Частота Найквиста — в цифровой обработке сигналов частота, равная половине частоты дискретизации. Из теоремы Котельникова следует, что при дискретизации аналогового сигнала потерь информации не будет только в том случае, если спектр (спектральная плотность) сигнала равен нулю выше частоты Найквиста. В противном случае при восстановлении аналогового сигнала будет иметь место наложение спектральных «хвостов» (подмена частот, маскировка частот), и форма восстановленного сигнала будет искажена. Если спектр сигнала не имеет составляющих выше частоты Найквиста, то он может быть (теоретически) продискретизирован и затем восстановлен без искажений. Фактически «оцифровка» сигнала (превращение аналогового сигнала в цифровой) сопряжена с квантованием отсчётов — каждый отсчёт записывается в виде цифрового кода конечной разрядности, в результате чего к отсчетам добавляются ошибки квантования (округления), при определенных условиях рассматриваемые как «шум квантования». Особенности выполнения арифметических операций в системе MATLAB. Использование оператора точка «.». Над вещественными числами и переменными типа double производятся арифметические операции: сложения +, вычитания -, умножения *, деления / и возведения в степень ^ . Приоритет в выполнении арифметических операций обычный. Операции одинакового приоритета выполняются в порядке слева на- право, но круглые скобки могут изменить этот порядок. Если нет необходимости видеть в командном окне результат вычисления некоторого выражения, то в конце введенного выражения следует поставить точку с запятой и только после этого нажать Enter. Оператор точка – это оператор который позволяет работать с массивами. Например: поэлементное деление массивов слева направо . / Синтаксис функций в MATLAB. В именах переменных (последовательностях латинских букв и цифр, начинающихся с буквы; знак _ относится к буквам) строчные и заглавные буквы отнюдь не тождественны! Если нужно выполнить команду без вывода результата, в конце команды ставится символ точки с запятой. Заголовок М-функции имеет вид: function [<список выходных переменных>]= <имя функции> (<список входных переменных>) например, функция вычисления факториала положительного числа и его обратной величины может быть описана файлом fact.m: function [f, g]=fact(n) % факториал и обратная величина f=prod (1:n); g=1/f; Запрограммировать медианный фильтр в системе MATLAB. Одним из наиболее простых примеров ранговой обработки изображений является медианная фильтрация. Преимуществом данного алгоритма является простота его реализации. К недостаткам же относится то, что сглаживание изображений с помощью медианной фильтрации приводит к устранению границ деталей изображения. Синтаксис: D=medfilt2(S, [m n]) Xd=medfilt2(Xs, ‘indexed’,...) Описание: Медианная фильтрация является частным случаем ранговой фильтрации. Функция D=medfilt2(S, [m n]) создает полутоновое изображение D, каждый пиксель которого формируется следующим образом. Пиксели исходного полутонового изображения S, соответствующие всем элементам маски фильтра размера m  n, составляют упорядоченную последовательность А. Пикселю D(r, с), где r и с – координаты текущего положения центрального элемента маски, присваивается значение медианы последовательности А. Операция применяется нерекурсивно для всех положений маски.Медианой упорядоченной последовательности A(i), где i=1...N, называется величина A((N + 1)/2), если N - нечетное, и (A(N/2) + A((N+2)/2))/2, если N - четное. Для того чтобы размеры изображений S и D были одинаковыми, при проведении вычислений изображение S временно дополняется необходимым количеством строк и столбцов нулевых пикселей. Формат представления данных результирующего изображения D совпадает с форматом исходного изображения S. Если вектор [m n] при вызове функции D=medfilt2(S) не задан, то в качестве маски фильтра используется маска размера 3 3.Функция Xd=medfilt2(Xs, 'indexed', ...) аналогична рассмотренной выше, но предназначена для обработки палитровых изображений. При проведении вычислений исходное изображение временно дополняется либо единицами при формате представления данных Xs–double, либо нулями при формате представления данных Xs–uint8. Медианная фильтрация может эффективно применяться для устранения импульсного шума. % Пример демонстрирует работу медианного фильтра. % Чтение исходного изображения и вывод его на экран. I=imread('bacteria.tif'); % название изображения и его формат imshow(l); % Медианная фильтрация. I=medfilt2(I); % Вывод на экран результата фильтрации. figure, imshow(I); Векторизация данных в MATLAB. Привести примеры использования векторизации данных. Язык программирования MATLAB рассчитан на обработку матричных данных, поэтому многие операторы и функции позволяют проводить операции с такими данными. Например, функция sin позволяет найти функцию синуса для всех элементов массива данных. Пользователь должен пользоваться данной возможностью, так как это позволяет улучшить читаемость текста программы и увеличить производительность. Например, вместо того, чтобы в цикле для всех элементов массива находить функцию синуса, можно ограничится одним выражением. Такие действия называются векторизацией. Пример: 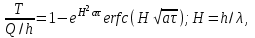 где τ - время, Q - тепловой поток, T - температура, h – коэффициент поверхностного теплообмена, λ - теплопроводность, a - температуропроводность. Далее приводится вариант, в котором используется возможность векторизации. Следует отметить использование оператора «.*», который выполняет поэлементное умножение элементов массива. function T = SI_STEP_NA2( time, diff, Q, cond, alf) H = alf / cond; T = Q/alf * ( 1 - exp( H^2 * diff * time) .* erfc( H * sqrt( diff * time))); Опишите способы создания матриц в MATLAB. Можно вводить матрицы в MATLAB несколькими способами: * вводить полный список элементов * загружать матрицы из внешних файлов * генерировать матрицы, используя встроенные функции * создавать матрицы с помощью ваших собственных функций в М-файлах Условия введения матрицы: * отделять элементы строки пробелами или запятыми * использовать точку с запятой ; для обозначения окончания каждой строки * окружать весь список элементов квадратными скобками, [ ]. 1) матрица Дюрера просто пишем: А = [16 3 2 13; 5 10 11 8; 967 12; 4 15 14 1] MATLAB отобразит матрицу, которую мы ввели, A = 16 3 2 13 5 10 11 8 9 6 7 12 4 15 14 1 2)Операцию конкатенации. Элементы массива набираются один за другим согласно их расположению в строках, в качестве разделителя строк используется точка с запятой. Введите с клавиатуры: » a=[1 2; 3 4; 5 6] Нажмите ENTER, получим: a = 1 2 3 4 5 6 3)Можно применить специальную функцию, обозначаемую двоеточием (операция формирования диапазона числовых значений). Через двоеточие следует набрать первое число диапазона, шаг (приращение) и конечное число диапазона. Например: » diap=3.7:0.3:8.974; 4) Операция индексации, прописывание по отдельности все элементы. Номер строки и столбца, на пересечении которых находится задаваемый элемент массива, указываются через запятую в круглых скобках. Например: » a(1,1)=1; a(1,2)=2; a(2,1)=3; » a(2,2)=4; a(3,1)=5; a(3,2)=6; Будет эффективнее, если до начала прописывания элементов массива, создать массив нужного размера функциями ones (m,n) или zeros(m,n),заполненный единицами или нулями (m – число строк, n – число столбцов).При вызове этих функций предварительно выделяется память под заданный размер массива, после этого постепенное прописывание элементов нужными значениями не требует перестройки структуры памяти, отведенной под массив. 5)Функция repmat - формирование массива из частей - использует преимущество векторизации. Она имеет три входных аргумента: массив A, количество строк М и столбцов N для вновь создаваемого массива. Функция repmat возвращает массив B , который использует массив A в качестве основы для построения блочной матрицы с количеством блоков MxN: A = [1 2 3; 4 5 6]; B = repmat(A, 2, 3); |