Линейные и нелинейные системы. Описание и примеры
 Скачать 1.16 Mb.
|
|
5 Статические и астатические системы Свойство астатизма является одним из важнейших свойств систем управления. По передаточной функции системы очень просто судить о наличии у нее этого свойства. И все же это свойство системы, а не передаточной функции. Поэтому и начнем рассуждения с качественной стороны дела. Свойство астатизма может быть по отношению к управляющему или возмущающему воздействию. По умолчанию подразумевается первый случай. Система называется астатической, если при стремлении управляющего воздействия к постоянной величине, отличной от нуля, сигнал ошибки стремится к нулю. Уточнение того, что постоянная величина, к которой стремится управляющее воздействие, отлична от нуля, потребовалось только потому, что в противном случае сигнал ошибки стремится к нулю вне зависимости от того, астатическая система или нет. Об астатизме системы легко судить по ее передаточной функции. Выясним условия, которым должна удовлетворять передаточная функция астатической системы. По теореме о начальных и конечных значениях условие равенства нулю предельного значения сигнала ошибки имеет вид:  .Условие же неравенства нулю предельного значения входного процесса имеет вид:  .Последнее неравенство возможно в случае, когда изображение Y (s ) можно представить в виде  ,таком что  .Подставим такое значение изображения по Лапласу входного воздействия в выражение предельного значения сигнала ошибки:  Так как второй сомножитель здесь не равен нулю, то условием равенства произведения в правой части последнего выражения является равенство нулю первого сомножителя. Говорят, что функция  имеет нуль n-го порядка ( ) в начале координат, если она может быть представлена в виде и  .Таким образом, система астатическая тогда и только тогда, когда ее передаточная функция по ошибке имеет нуль какого-либо порядка в начале координат. Суждение об астатизме замкнутой системы ведется обычно по виду передаточной функции разомкнутой системы. Под передаточной функцией разомкнутой системы понимается передаточная функция той последовательности операторов, которая начинается с выхода сравнивающего звена и кончается одним из входов в это звено. Передаточная функция замкнутой системы по ошибке 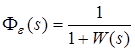достаточно просто выражается через передаточную функцию разомкнутой системы  :  .Не трудно доказать, что передаточная функция по ошибке имеет нуль n–го порядка в начале координат, когда передаточная функция разомкнутой системы имеет полюс того же порядка в начале координат. Действительно, пусть это условие выполнено, т.е. возможно представление передаточной функции разомкнутой системы в виде  , ( ).Тогда 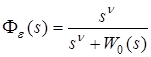 ,  .Строго говоря, если передаточная функция по ошибке имеет нуль n–го порядка в начале координат, то можно говорить об астатизме того же порядка системы управления. Астатизм выше первого порядка редко встречается и его трудно организовать, поэтому, говоря об астатизме, имеют в виду, как правило, именно астатизм первого порядка. Все ранее сказанное об астатизме имело отношение к астатизму по управляющему воздействию. Если в качестве входного воздействия рассматривать возмущающее воздействие, то приведенные выше определения будут относиться к астатизму по возмущения, а не по управлению. Пример. Простейшим примером воздействия, стремящегося к постоянному, не равному нулю значению, является, так называемое единичное ступенчатое воздействие. В дальнейшем оно будет рассмотрено достаточно подробно, а пока только скажем, что оно равно единице при положительных значениях моментов времени и нулю при отрицательных. Преобразование Лапласа такой функции равно 1/s . На рисунке 5 показана кривой 1 показана реакция астатической системы, а кривой 2 – реакция статической системы на единичное ступенчатое воздействие. Самым существенным здесь является то, что в первом случае величина установившейся ошибки e равна нулю, а во втором – некоторой постоянной величине. 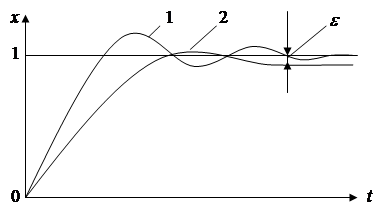 Рисунок 5 – Статические и астатические системы Различие между статическими и астатическими системами принципиально с теоретической точки зрения, хотя с практической это не совсем так. Действительно, если значение передаточной функций по ошибке в начале координат пренебрежимо мало, то следует ожидать столь же малым значение установившейся ошибки. |