Линейные и нелинейные системы. Описание и примеры
 Скачать 1.16 Mb.
|
|
31 Показатели качества системы Автоматические системы управления должны быть не только устойчивыми, но и обеспечивать качество процесса управления. Основные наиболее существенные требования к качеству управления, которые позволяют оценить работу почти всех систем управления, называют показателями процесса управления. Они характеризуют поведение системы в переходном процессе. Показателями качества будет время регулирования, перерегулирование, колебательность процесса, установившаяся ошибка, характер затухания переходного процесса, запас устойчивости. Качество процессов регулирования обычно оценивают по переходной функции, которая представляет собой реакцию системы на внешнее воздействие типа единичного скачка. Для следящих систем и программного регулирования переходную функцию рассматривают по отношению к задающему воздействию, а для систем стабилизации – по отношению к возмущению. 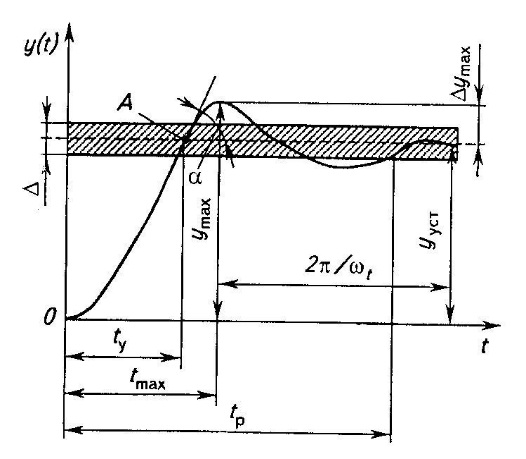 Рисунок 1. Определение показателей качества регулирования по переходной характеристике. На рис. 1 изображена переходная функция по которой можно определить основные показатели качества переходного процесса: время регулирования, перерегулирование и др. Время регулирования определяет длительность переходного процесса. Теоретически переходной процесс длится бесконечно долго, однако практически его считают законченным, как только отклонение регулируемой величины от нового ее установившегося значения не будет превышать допустимых пределов. Временем регулирования называют минимальное время, по истечении которого, начиная с момента начала действия входного сигнала, выходная переменная отклоняется от установившегося значения на величину, не превышающую некоторую заданную постоянную величину 0,5. Время регулирования характеризует быстродействие системы. Быстродействие может характеризоваться и временем достижения переходной функцией нового установившегося значения, и временем достижения максимального значения. Перерегулированием называется максимальное отклонение управляемой величины от заданного значения и выраженной в процентах. Время регулирования и перерегулирования взаимосвязаны. Так, перерегулирование зависит от скорости изменения регулируемой величины, которая графически представляет собой тангенс угла наклона α (альфа) касательной в точке А к кривой (рисунок 1). Чем больше эта скорость, тем больше перерегулирование. Поэтому для его уменьшения необходимо уменьшить скорость, с которой система подходит к новому установившемуся состоянию. Но это приведет к увеличению времени регулирования. Если система подходит к установившемуся состоянию с нулевой скоростью, то перерегулирования вообще не будет, но время регулирования значительно увеличится (рисунок 2). 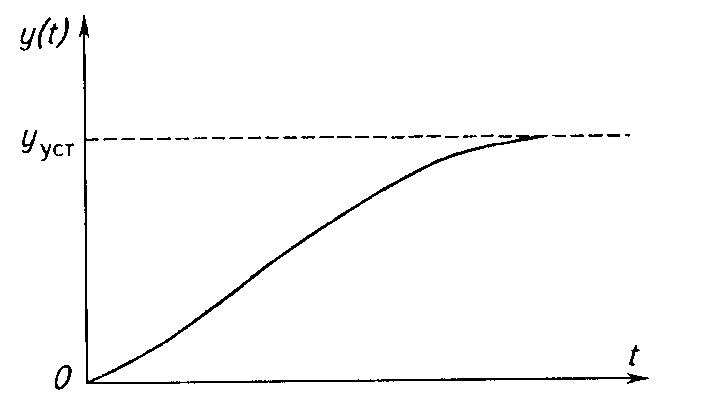 Рисунок 2. Переходная характеристика системы автоматического регулирования без перерегулирования. Значения времени регулирования и перерегулирования часто задают в качестве исходных данных для синтеза корректирующих устройств, поскольку правильным выбором и настройкой последних обеспечивается подавление нежелательных колебаний регулируемой величины в переходном процессе. Для некоторых систем перерегулирование вообще недопустимо, например для систем автоматического регулирования физических величин в процессах, связанных с приготовлением продуктов. Необходимо так же иметь в виду, что стремление уменьшить время регулирования приводит к увеличению мощности исполнительного устройства. Колебательность процесса характеризуется числом колебаний управляемой величины за время регулирования. Количественно колебательность оценивается по логарифмическому декременту затухания, который представляет собой натуральный логарифм отношения двух последующих амплитуд отклонений управляемой величины одного направления. Чем больше логарифмический декремент затухания, тем быстрее происходит затухание переходного процесса. Установившаяся ошибка показывает точность управления в установившемся режиме. Она ровняется разности между заданным значением управляемой величины и ее установившимся значением при нормальной нагрузке. Характер затухания переходного процесса позволяет классифицировать переходные процессы в системах управления и выделить среди их многообразия четыре основных вида (рисунок 3): колебательный процесс (кривая 1) – ему присуще несколько значений перерегулирования; малоколебательный процесс (кривая 2) – процесс с одним перерегулированием; монотонный процесс (кривая 4), при котором скорость изменения управляемой величины не изменяет знака в течение всего времени регулирования; апериодический процесс (кривая 3) – процесс, когда управляемая величина меньше ее установившегося значения с точностью до зоны нечувствительности регулятора при всех значениях времени регулирования. 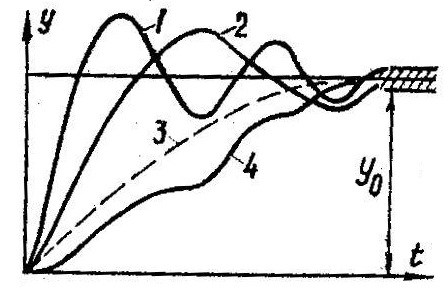 Рисунок 3. Основные виды характеристик переходных процессов автоматических систем регулирования при типовом единичном воздействии. Запас устойчивости – это физическая сущность и методы определения этого показателя качества управления. Показатели, которые характеризуют качество работы системы в переходном режиме, делят на прямые и косвенные. Прямые показатели – это числовые оценки качества, получаемые непосредственно по переходной характеристике. Для получения прямых показателей качества необходимо иметь кривую переходного процесса, которую можно построить по структурной схеме или дифференциальному уравнению систем автоматического регулирования, используя аналоговые вычислительные машины или компьютеры. Косвенные оценки качества переходного процесса позволяют определить некоторые особенности переходного процесса и установить влияние параметров системы на качество переходных процессов. К косвенным показателям качества относятся корневые, частотные и интегральные оценки. Рассмотрим корневые оценки качества. Геометрически степень устойчивости можно определить как расстояние на плоскости от мнимой оси до ближайшего к ней корня или ближайшей пары комплексных корней (рисунок 4). 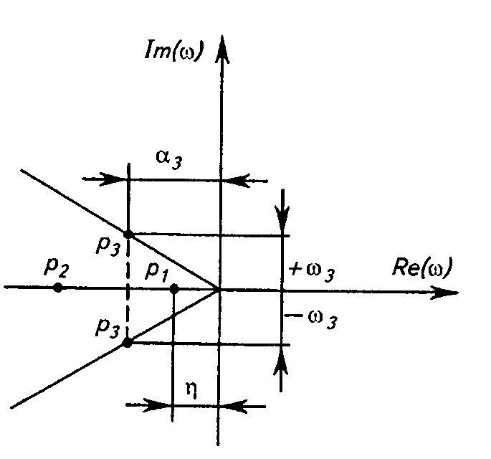 Рисунок 4. Корневые оценки качества систем автоматического регулирования. Понятие степени устойчивости используют для синтеза систем автоматического регулирования. Рассмотрим частотные оценки качества. При гармонических воздействиях качество систем автоматического регулирования принято оценивать по частотным характеристикам. Для этого используют следующие величины: показатель колебательности и частоту среза. Показатель колебательности – это отношение максимального значения амплитудно-частотной характеристики замкнутой системы к ее значению при частоте равной нулю. Частота среза – это частота при которой амплитудно-частотная характеристика равна единице. Косвенно она характеризует длительность переходного процесса. Рассмотрим интегральные оценки качества. По кривой переходного процесса можно оценить качество процесса регулирования в данной системе. Косвенно оценить качество регулирования можно по площади между кривой переходного процесса и линией установившегося режима. В данном случае критерием качества будет определенный интеграл по времени от функции, характеризующей разницу между действительным и заданным значениями регулируемой величины. 32. Что такое передаточная функция? Функция W(p) называется передаточной функцией объекта, который описывается уравнением:  Она полностью описывает связи между выходом и входом объекта при нулевых начальных условиях, но не учитывает его внутреннее устройство. Передаточная функция W(p) называется правильной, если степень ее числителя не больше, чем степень знаменателя; строго правильной, если степень числителя меньше степени знаменателя; неправильной, если степень числителя больше, чем степень знаменателя. Нулями передаточной функции называются корни ее числителя, а полюсами – корни знаменателя. 3 Передаточные функции основных видов соединений звеньев Системы, как правило, состоят из подсистем или звеньев по терминологии теории автоматического управления. Зная передаточные функции звеньев не трудно вычислить передаточную функцию системы. Для этого пользуются выражениями передаточных функций основных видов соединений звеньев. Большая часть из них очевидна, тем не менее, рассмотрим все три основных вида соединений. Последовательное соединение. Структурная схема последовательного соединения двух звеньев приведена на рисунке 1, где приведены изображения координат, являющихся функциями времени. 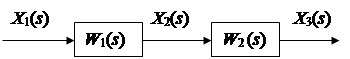 Рисунок 1 – Последовательное соединение звеньев Не трудно выразить преобразование Лапласа выходной координаты через преобразование Лапласа входной координаты и выражения передаточных функций отдельных звеньев  .Отсюда следует, что передаточная функция последовательного соединения звеньев равна произведению передаточных функций этих звеньев.  .Параллельное соединение. Структурная схема данного соединения приведена на рисунке 2. 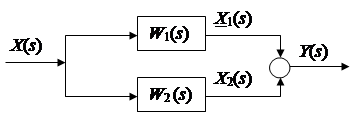 Рисунок 2 – Параллельное соединение Выразим преобразование Лапласа выходной координаты через преобразование Лапласа входной координаты и выражения передаточных функций отдельных звеньев параллельного соединения, под которым понимается суммирование выходных координат этих звеньев:  .Отсюда следует, что передаточная функция параллельного соединения звеньев равна алгебраической сумме передаточных функций этих звеньев.  .Соединение по схеме обратной связи. Как и сам принцип обратной связи, эта схема соединения является важнейшей для теории автоматического управления. Она показана на рисунке 3.3.  Рисунок 3 – Соединение по схеме обратной связи Выразим преобразование Лапласа выходной координаты через преобразование Лапласа входной координаты и выражения передаточных функций отдельных звеньев рассматриваемого соединения. Сначала составим уравнение связи между изображениями различных координат:  ,а затем и изображения выходной координаты через изображение входной: 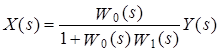 .Таким образом, выражение передаточной функции замкнутой системы 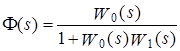 выражается через передаточную функцию прямой цепи и обратной связи  дробью вида .Здесь рассматривался только случай отрицательной обратной связи. Случай положительной обратной связи в теории автоматического управления практически не используется. Поэтому он и остался вне поля зрения, хотя повторить все выкладки в случае, когда сигнал обратной связи не вычитается из входного сигнала, а складывается с ним, не представляет труда. В связи с широким использованием этого типа соединения последняя формула читается многими способами, самый распространенный из которых: «передаточная функция замкнутой системы равна передаточной функции прямой цепи, деленной на единицу плюс передаточная функция разомкнутой цепи». Полезность такой словесной формулировки проявляется в тех случаях, когда структурная схема замкнутой системы несколько отличается от только что рассмотренной. В этом случае можно и не повторять вывод формулы замыкания, а только уточнить, что понимать в данном конкретном случае под передаточной функцией прямой цепи и передаточной функцией разомкнутой цепи. В качестве примера рассмотрим определение передаточной функции (замкнутой системы) по ошибке 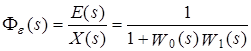 . Под передаточной функцией по ошибке понимается отношение изображения сигнала рассогласования (ошибки) к изображению входного сигнала (при нулевых, конечно, условиях). Если повторить вывод формулы замыкания для определения коэффициента пропорциональности между изображением сигнала ошибки  и входного сигнала  , то получим, что .Это же самое можно было бы получить, используя словесное описание формулы замыкания, если считать выходной координатой сигнал ошибки. Действительно, в прямой цепи в этом случае нет никакого преобразования или, что то же самое, единичное преобразование, а передаточная функция разомкнутой цепи та же самая, что и в рассмотренном ранее случае. В другом часто встречающемся частном случае единичной обратной связи передаточные функции замкнутой системы и по ошибке имеют вид: 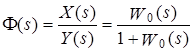 ,  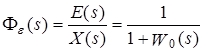.4 Передаточные функции по управлению и по возмущению До сих пор рассматривались системы с одним входом и одним выходом, т.е. простейший вид одномерных систем. Даже в рамках одномерных систем входных процессов может быть несколько. В классической теории управления нередко рассматриваются системы с двумя входными воздействиями: управляющим и возмущающим, полезным сигналом и помехой. Аппарат передаточных функций и в этом случае оказывается полезным. Для примера рассмотрим случай системы с обратной связью, в которой наряду с управляющим воздействием имеется возмущающее. Приведем ее структурную схему и соответствующую систему дифференциальных уравнений. В теории автоматического управления, как правило, отдается предпочтение первой из этих двух эквивалентных форм описания систем. Точнее, основную часть информации о замкнутой системе приводят в виде структурной схемы, а недостающую – в виде дифференциальных уравнений или передаточных функций. Итак, пусть структурная схема системы такая, как она изображена на рисунке 4.  Рисунок 4 – Структурная схема системы с двумя воздействиями Эта же система пусть описывается системой уравнений: уравнением сравнивающего звена  ;уравнением регулятора  , ( );уравнением объекта регулирования  , ( ).Здесь p – символ дифференцирования, B , N , D , M , C – полиномы от p . Другими словами, два последних уравнения являются, в действительности дифференциальными уравнения, только записанными в символьной форме. При нулевых начальных условиях применим преобразования Лапласа к каждой части уравнения этой системы уравнений. Тем самым будут получены те же самые уравнения в изображениях: уравнение сравнивающего звена  ;уравнения регулятора 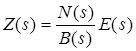 ,  ;уравнения объекта 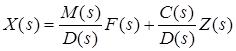 ,  ;и выражения соответствующих передаточных функций, с использованием которых можно наиболее наглядным образом представить взаимосвязь между входом и выходом в каждом звене: передаточную функцию регулятора 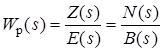 : ,  ;передаточную функцию объекта по управлению 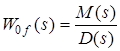 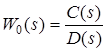и по возмущению  : , ,  .Проще всего дать определение этих передаточных функций в виде отношения полиномов, коэффициенты которых определяются соответствующими коэффициентами дифференциальных уравнений, как это только что проделано. Однако полезней всего определить их как отношение изображений по Лапласу соответствующих координат не только при нулевых начальных условиях, но и при равенстве нулю всех остальных координат, которые в рассматриваемой ситуации не рассматривается как входная координата. Например, передаточной функцией объекта по управлению является отношение изображений выходной координаты объекта к изображению входной координаты объекта при нулевых начальных условиях на упомянутые координаты и равенстве нулю возмущающего воздействия f (t ). Исключая переменные и  из системы уравнений связывающей значения всех переменных (в изображениях), получим уравнение связи Определим теперь выражение изображения выходной координаты замкнутой системы через изображения входных координат (управляющего и возмущающего воздействий) 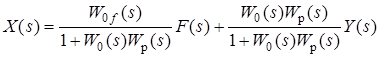 .Отсюда видно, что передаточная функция замкнутой системы по управлению имеет в точности такой же вид, как если бы возмущение, вообще, отсутствовало 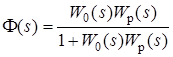 ,а передаточная функция замкнутой системы по возмущению имеет вид: 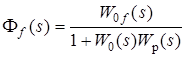 .Ее можно определить точно так же, как и ранее упомянутую, если предположить отсутствие управляющего воздействия. Вообще, в классической теории управления все координаты равноправны. Хотя считается, что в данной теории рассматриваются системы с одной входной и одной выходной координатой, имеется некоторый выбор среди небольшого числа координат, какую из них считать входной, а какую – выходной. По умолчанию предполагается, что входной координатой является управляющее воздействие, а выходной – регулируемая или управляемая координата. Всякое отклонение от этого варианта уточняется. Например, говоря о передаточной функции по ошибке, подразумевается, что входной координатой считается управляющее воздействие, а выходной – координата ошибки. Аналогично, говоря о передаточной функции по возмущению, имеют в виду, что входной координатой является возмущение, а выходной – управляемая координата. |