Линейные и нелинейные системы. Описание и примеры

• Название: Линейные и нелинейные системы. Описание и примеры
• Дата: 15.03.2022
• Размер: 1.16 Mb.
• Имя файла: OTVETY.docx
• Тип: Документы; #397019
• страница: 4 из 6

27. ЛАЧХ системы. Полоса пропускания, частота среза системы.

ЛАЧХ – это зависимость модуля коэффициента усиления (напряжения, тока или мощности) устройства от частоты в логарифмическом масштабе.

• 
  По оси абсцисс откладывается частота в логарифмическом масштабе.
  
• 
  По оси ординат откладывается амплитуда выходного сигнала в логарифмических безразмерных величинах.
  

ЛФЧХ – это зависимость фазы выходного сигнала от частоты в полулогарифмическом масштабе

• по оси абсцисс откладывается частота в логарифмическом масштабе

• по оси ординат откладывается выходная фаза в угловых градусах или радианах.

По ЛАЧХ и ЛФЧХ определяется запас устойчивости по амплитуде ΔL (дБ) и запас устойчивости по фазе Δφ (град.).

Способ определения запасов устойчивости по ЛАЧХ и ЛФЧХ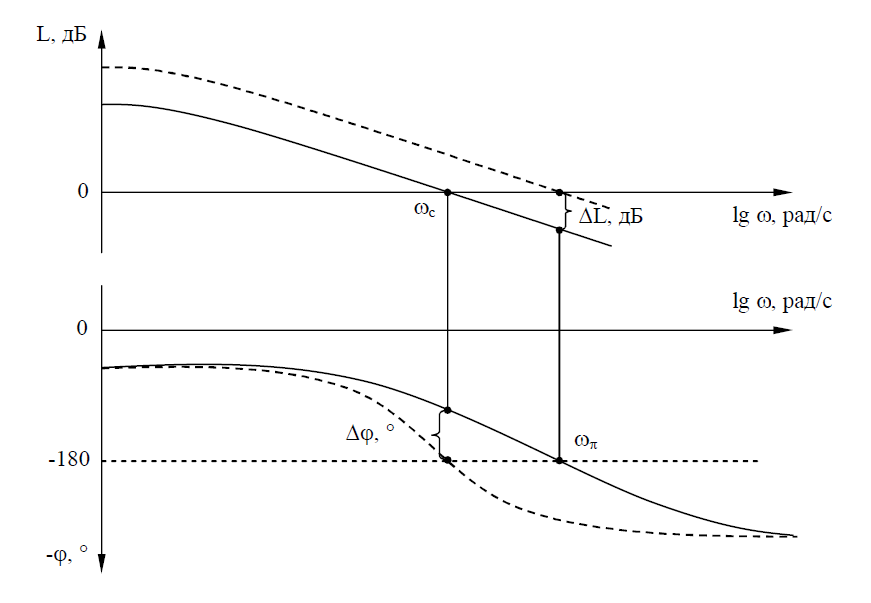

• 
  из точки пересечения ЛФЧХ, при окончательном ее спаде, c линией, проведенной на уровне −180° (частота фазового сдвига), отнимается перпендикуляр до пересечения с ЛАЧХ. Расстояние от этой точки до оси абсцисс даст искомое значение запаса устойчивости по амплитуде (ΔL, дБ);
  
• 
  из точки пересечения ЛАХ оси абсцисс (частота среза) опускается перпендикуляр до пересечения с ЛФХ, расстояние от этой точки до уровня −180° даст искомое значение запаса устойчивости по фазе (Δφ°).
  

Запас устойчивости по амплитуде – отклонение ЛАЧХ от оси частот при частоте, соответствующей первому отрицательному переходу ЛФЧХ через уровень –π.

Запас устойчивости по фазе - отклонение ЛФЧХ от уровня –𝜋при значении частоты ω, равном частоте среза. Графически запас по фазе определяется как разность между фазой равной π радиан (180°) и фазой на частоте среза.

Частота среза — частота, выше или ниже которой мощность выходного сигнала электронной схемы уменьшается вполовину от мощности в полосе пропускания. Амплитудно-частотная характеристика на частоте среза имеет спад до уровня примерно -3 дБ относительно уровня на полосе пропускания. это точка, начиная с которой более высокочастотные колебания перестают проходить через фильтр.

Полоса пропускания (прозрачности) — диапазон частот, в пределах которого амплитудно-частотная характеристика (АЧХ) устройства достаточно равномерна для того, чтобы обеспечить передачу сигнала без существенного искажения его формы.

Полосой пропускания замкнутой системы обычно называют полосу частот от нуля до частоты, соответствующей половинному значению мощности и иногда именуемой частотой среза.

28 Параметрический резонанс

В классической линейной теории при выводе дифференциальных уравнений, а также при переходе к анализу систем управления на языке передаточных функций, считается, что параметры, описывающие систему, не изменяются со временем (стационарны). Например, при составлении "классического" дифференциального уравнения маятника принималось, что

его масса и длина постоянны. Естественно, это предположение является некоторой идеализацией, так как нет такого физического объекта, который не был бы подвластен времени. Это медленное изменение (дрейф) параметров под действием, например, старения, обычно мало заметно на

гораздо более коротких временах интересующих нас движений системы, и потому им пренебрегают. Однако в некоторых физических системах изменения этих параметров носят более чем явный характер и совершаются со скоростями, сравнимыми со скоростями движения самой системы.

Например, качели с раскачивающимся на них человеком можно рассматривать как обыкновенный маятник, но с меняющимся во времени параметром – его длиной.

Многократные наблюдения нештатной, неустойчивой работы системы, а зачастую просто катастрофических разрушений при определенной частоте и амплитуде изменения некоторого параметра системы привели к необходимости поиска объяснения этого явления и расчета условий его возникновения. Кроме того, умение рассчитывать условие параметрического резонанса позволило бы использовать его в благих целях.

Важность умения рассчитывать параметрические явления подчеркивает и тот факт, что к ним сводится анализ устойчивости периодических процессов и нелинейных систем управления

Широко распространенным приемом генерирования колебаний в электротехнике и радиотехнике служит электрический RLC контур с периодически изменяющейся емкостью, как показано на рис. 1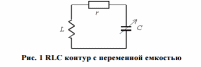



Для применения частотного критерия устойчивости необходимо перейти к представлению системы, похожему на то, которое использовалось для применения критерия Найквиста, см. рис. 2.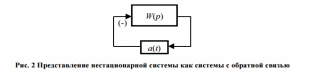



Однако принципиальная особенность данной ситуации заключается в том, что элемент a(t) меняется со временем, а значит его "передаточная функция" изменяется.

Ошибка, которая может стоить аварии, произойдет, если не считать данную задачу принципиально новой, ограничиваясь стандартной проверкой устойчивости для нескольких фиксированных значений параметра из заданного диапазона.

Для корректной замены нестационарного элемента на эквивалентную передаточную функцию необходимо провести процедуру параметрической стационаризации.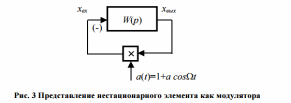



Принципиальной особенностью наличия в системе нестационарного элемента будет то, что после прохождения через него сигнала xвых , спектр качественно изменится. В колебаниях системы появятся новые частоты (при прохождении сигнала через элемент W(p) этого не происходит!). Именно по этим частотам может нарушиться устойчивость замкнутой системы. Разумеется, учесть все (а их, вообще говоря, бесконечное количество) появившиеся частоты не представляется возможным. Однако этого и не требуется, поскольку обычно любой реальный линейный элемент W(p) является фильтром низких частот, его АЧХ с увеличением частоты падает.

Это предположение называют гипотезой фильтра. Поэтому ограничиваются анализом устойчивости по нескольким первым гармоникам.

Можно показать, что периодичность изменения параметра приводит к возможности возбуждения на выходе системы периодических колебаний с частотой, кратной частоте изменения параметра W. Такие колебания называются параметрическими.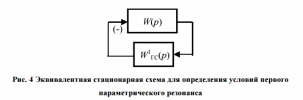



Теперь для суждения об устойчивости или неустойчивости замкнутой системы достаточно оценить поведение годографа разомкнутой системы WР(jW) = W(jW/ 2)W

Итак, критерий возникновения в контуре колебаний первого параметрического резонанса формулируется следующим образом: Если годограф – [W(jw)]–1 пересекает окружность W1ГС(jj), то в системе возможно возникновение параметрических колебаний. Точки пересечения определяют границы частотного диапазона, в котором возникает соответствующий периодический режим (см. рис. 5).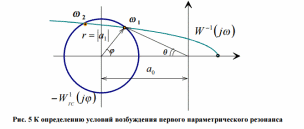



29 Автоколебания системы

Автоколебания - незатухающие колебания за счет действия источника энергии, не обладающего колебательными свойствами (периодичностью). Примеры: часы, орган, духовые инструменты, сердечно-сосудистая система, паровые машины и двигатели внутреннего сгорания и т.д.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Автоколебания принципиально отличаются от других колебательных процессов в тем, что для их поддержания не требуется колебательных воздействий извне.

В некоторых системах автоколебания возникают "самопроизвольно" - без начального толчка, в других для возникновения автоколебаний необходим конечный начальный толчок,

Примеры автоколебаний: Колебания скрипичной струны при движении смычка, Колебания тока в радиотехническом генераторе, Колебания воздуха в органной трубе, Колебания маятника в часах и т.п.

Любая автоколебательная система состоит из 4 частей:

1. 
   колебательная система;
   
2. 
   источник энергии, компенсирующий потери энергии на преодоление сопротивления;
   
3. 
   клапан – устройство, регулирующее поступление энергии в колебательную систему определенными порциями и в определенный промежуток времени;
   

обратная связь – устройство для обратного воздействия автоколебательной системы на клапан, управляющее работой клапана за счет процессов в самой колебательной системе

30 Вынужденные колебания нелинейной системы

Симметричные одночастотные вынужденные колебания

Проблема анализа вынужденных колебаний нелинейных систем вообще является весьма сложной и многообразной. Поскольку принцип наложения решений (суперпозиция) здесь неприменим, то, вообще говоря, нельзя складывать частные решения при различных внешних воздействиях, найденных по отдельности, а также складывать свободные и вынужденные колебания. Особое нелинейное сложение решений возможно в случае, если решения разделяются по степени медленности протекания их во времени (т. е. по значению возможных частот колебаний). При этом каждое из складываемых решений существенно зависело от другого, а именно амплитуда автоколебаний существенно зависела от величины смещения, характеризующей медленно протекающие процессы. Такого же рода разделение решений для вынужденных колебаний будет рассмотрено ниже, где появится возможность рассмотрения нелинейных двухчастотных колебаний с большой разностью частот.

Не касаясь сложных форм вынужденных колебаний нелинейных систем (хотя их исследование также имеет большое практическое значение), ограничимся определением одночастотных вынужденных колебаний, когда колебания системы происходят с частотой внешнего периодического воздействия. При рассмотрении вынужденных колебаний во многих случаях возникают ограничения, накладываемые на амплитуду и частоту внешнего периодического воздействия (зависящие также и от параметров системы) и обусловливающие существование одночастотных вынужденных колебаний в нелинейной системе. Будем их кратко называть условиями захватывания (в указанном широком смысле). Особое значение эти условия приобретают для автоколебательных систем при частотах, близких к частоте автоколебаний и выше.

Итак, пусть имеется некоторая нелинейная автоматическая система, в любом месте которой приложено внешнее синусоидальное воздействие



Пусть уравнение динамики системы приведено к виду



Выполнение выводимых ниже условий захватывания (где это необходимо) позволяет в первом приближении искать решение для установившихся вынужденных колебаний системы в синусоидальной форме



где искомыми неизвестными постоянными будут амплитуда и сдвиг фазы φ, в то время как частота ω_В здесь задана выражением (21.1).

Чтобы иметь возможность применить общий подход к решению задачи выразим в уравнении (21.2) переменную через х. Согласно (21.1)



Отсюда, принимая во внимание выражение (21.3) для х и выражение для его производной



окончательно получаем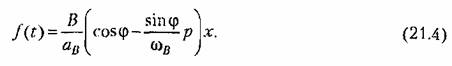



Подставив это выражение в заданное дифференциальное уравнение системы (21.2), получим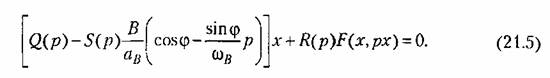



Таким образом, неоднородное нелинейное уравнение (21.2) при заданном внешнем воздействии (21.1) и предполагаемой форме решения (21.3) сведено к однородному нелинейному уравнению (21.5), содержащему добавочный член в левой части.

Заданная нелинейность 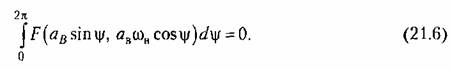 должна допускать симметричные колебания, т. е. должно выполняться условие



Итак, получив для определения вынужденных колебаний однородное уравнение (21.5), можно произвести гармоническую линеаризацию нелинейности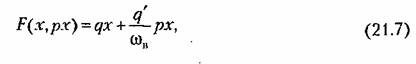



где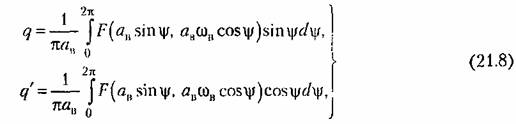



причем согласно (21.3)



что, однако, не влияет на результат вычисления q и q^’. Поэтому при определении симметричных однозначных вынужденных колебаний можно произвести замну а, ω и а_В, ω_В. Таким образом, для каждой нелинейности в общем случае получаются зависимости



а во многих частных случаях



В результате из (21.5) и (21.7) получаем характеристическое уравнение для первого приближения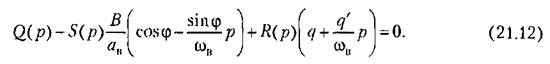



Подставляя сюда чисто мнимое значение 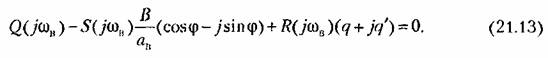, что соответствует отысканию синусоидального решения (21.3), получаем



Замечая, что



из уравнения (21.13) находим, что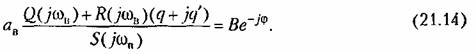



Возможны два метода дальнейшего решения задачи. Эти методы остаются справедливыми и для нелинейных систем с временным запаздыванием т, когда выражение (21.14) принимает вид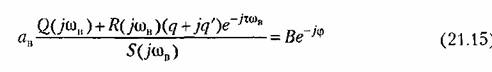

 

или другой аналогичный вид, содержащий .

Г 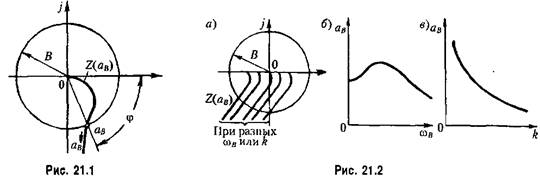рафический метод. Для каждого значения частоты при заданных параметрах системы на комплексной плоскости строится кривая (рис. 21.1)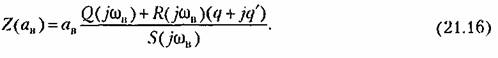



Эта кривая соответствует левой части равенства (21.14). Правая же часть (21.14) изобразится в виде окружности радиуса В. Пересечение ее с кривой дает решение задачи, причем в точке пересечения по дуге окружности определяется фазовый сдвиг φ, а по кривой - величина амплитуды а_Ввынужденных колебаний.

Зависимость амплитуды вынужденных колебаний а_В от частоты ω_В (рис.21.2, б) можно получить, если на рис. 21.1 начертить серию кривых при разных постоянных значениях ω_В (рис. 21.2, а). Таким же путем, строя кривые при разных постоянных значениях какого-нибудь параметра k (рис. 21.2, а), можно определить зависимость а_Вот любого параметра системы k (рис. 21.2, в), входящего в выражение (21.1) для .



Для отыскания зависимости а_В от амплитуды внешнего воздействия В нужно нанести серию концентрических окружностей разных радиусов В (рис. 21.3, а). при этом возможны два случая: 1) когда имеется точка пересечения окружности с кривой 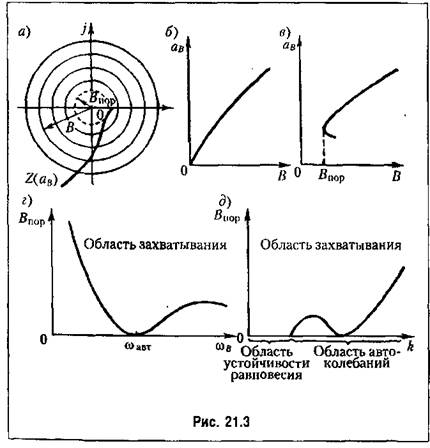при любой величине радиуса В. Начиная от нуля, что дает зависимость а_В (В), например в виде рис. 21.3, б; 2) когда точка пересечения окружности с кривой существует только при значениях радиуса В, превышающих некоторое пороговое значение В_пор (рис. 21.3, а), что приводит к зависимости а_В (В) типа рис. 21.3, в.



Графическое определение   ясно из чертежа. Можно построить зависимость пороговой амплитуды  внешнего воздействия от частоты ω_В при заданных параметрах системы (рис. 21.3, г) или от любого параметра k при данной частоте ω_В (рис. 21.3, д). Последнюю зависимость можно найти с помощью (рис. 21.3, а) построенного для серии кривых   , соответствующих различным k.

Рассмотренный второй случай, когда система переходит на одночастотные колебания с частотой ω_В только при  наблюдается чаще всего в таких нелинейных системах, которые до приложения внешнего периодического воздействия работают в автоколебательном режиме. При этом величина   обращается в нуль в том случае, когда частота  ω_В совпадает с частотой автоколебаний  данной системы ω_П  (рис. 21.3, г). равно нулю обычно также в области отсутствия автоколебаний (область устойчивости равновесия системы, рис. 21.3, д).

Тогда выше кривых на( рис. 21.3, г, д)  будут лежать значения амплитуды В внешнего воздействия, при которых существует одночастотный режим вынужденных колебаний с частотой  ω_В (область захватывания), а при значениях, лежащих ниже кривой, будет иметь место более сложное вынужденное движение системы. Это и является определением (пока графическим) условий захватывания, о которых говорилось выше.