Информационные технологии в психологии. Синергия.. IT в психологии. Литература по теме Тема Информационная безопасность и защита данных
 Скачать 1.49 Mb. Скачать 1.49 Mb.
|
|
Тема 7. (Часть 2). Сбор и обработка данных психодиагностических исследований с помощью программы MS Excel Цели и задачи: Цели и задачиизученияданной темы приобретение навыков использования электронных таблиц MS Excel в профессиональной деятельности психолога. В результате успешного изучения темы Вы: Узнаете: · применение электронных таблиц в практической деятельности психолога; · статистическая обработка экспериментальных данных. Приобретете следующие профессиональные компетенции: · сбор, обработка и анализ данных в профессиональной деятельности. В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях: Медиана — это элемент выборки, число элементов со значениями больше и меньше которого – равны. Мода — вычисляет количество наиболее часто встречающихся значений в выборке (наиболее вероятная величина). Дисперсия – позволяет оценить дисперсию по выборочным данным —степень разброса элементов выборки относительно среднего значения. Эксцесс – степень выраженности хвостов распределения, т.е. частоты появления величин, удаленных от среднего значения. Асимметрия указывает на отклонение распределения от нормального. Гистограмма геометрическое изображение эмпирической функции плотности вероятности некоторой случайной величины, построенное по выборке. Корреляция (коэффициент линейной корреляции) - позволяет исследовать тесноту связи, т.е. степень разброса точек от линии. Значения, равные 1 или -1 говорят о линейной связи величин, значение 0 – о полной отсутствии связи. Вопросы темы: 3. Сбор и первичная обработка результатов психодиагностических исследований в программе MS Excel. 4. Статистический анализ экспериментальных данных в MS Excel. Теоретический материал Вопрос 3. Сбор и первичная обработка результатов психодиагностических исследований в программе MS Excel. В настоящее время существует большое количество программного обеспечения для проведения психологического тестирования. Однако, не все психологи, работающие, в сфере образования имеют к ним доступ. Наиболее доступной является программа MS Excel, обладающая широкими возможностями для обработки данных и графического представления результатов. Рассмотрим обработку стандартных исследований с помощью MS Excel. Пример: Методика изучения межличностных отношений в младших классах. Ученикам предлагается расселить по домикам - конвертам - всех учащихся класса (их имена и фамилии написаны на отдельных карточках). Домики разные: дворец (1 выбор), квартира (2 выбор), изба (3 выбор), шалаш (4 выбор). После чего каждый ребенок подписывает свои конверты (4 шт.) и дает их психологу. Эти данные заносят в таблицу, используя цифры 1,2,3,4, соответственно выбору (Табл. 6). Для расчета социального статуса С используется формула: Сi= (4*Ч1+3*Ч2+2*Ч2+1*Ч1)/(n-1), где Ч1 –частота выбора варианта «дворец» и т.д. i-му ученику; n – число учеников, участвующих в опросе. Таблица 6. Данные опроса учеников по методике изучения межличностных отношений 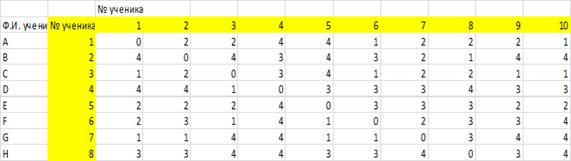 Для обработки результатов используем функцию СЧЕТЕСЛИ(), которая позволяет подсчитывать, сколько раз встречается выбранное число в диапазоне. Для этого ниже столбика «№ученика» запишем значения критерия отбора (1, 2, 3, 4) (Таблица) и вставим функцию для расчета. Чтобы формулу можно было бы скопировать на всю таблицу, используем смешанные ссылки: для границ диапазонов зафиксируем номера строк, а для критерия – номер столбца (Рис. 23). 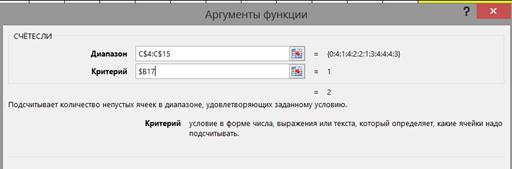 Рис. 23. Окно мастера функций СЧЕТЕСЛИ(). В нашем случае в поле Диапазон вводятся границы столбца с результатами оценки учениками ученика № 1. Чтобы границы диапазона по горизонтали не сдвигались при копировании, значения строк фиксируется абсолютной ссылкой. Аналогично, фиксируется столбец с значениями критерия (1, 3, …). Теперь в ячейке С17 будет сосчитано, сколько учеников выбрало для ученика №1 дворец, в ячейке С18 – квартиру, и т.д. В ячейках D17: D20 будут записаны аналогичные данные про ученика №2. Согласно методике, вводим в ячейку С21 формулу =(C17*4+C18*3+C19*2+C20*1)/(12-1), т.к. опрошено 12 детей. Копируем формулу на все столбцы и применяем условное форматирование с помощью значков (Таблица 4). На листе сразу видны проблемные дети. Составим итоговый отчет. На новый лист копируем столбец с фамилиями детей. Теперь рядом нужно поместить результаты исследования. Выделяем результирующую строчку и копируем. Выделяем результирующую строчку С21:О21 и копируем. Ее нужно вставить правее столбца с фамилиями. Для этого строку нужно транспонировать в столбец и вставлять рассчитанные значения, а не формулы. В этом случае вместо команды Вставить используется Специальная вставка, из контекстного меню. На рис. 24 показаны опции, которые надо установить в диалоговом окне команды Специальная вставка. Вы познакомились с некоторыми приемами обработки таблиц с данными тестов, опросов и пр. Таблица 3. Расчет частот оценок ученика одноклассниками 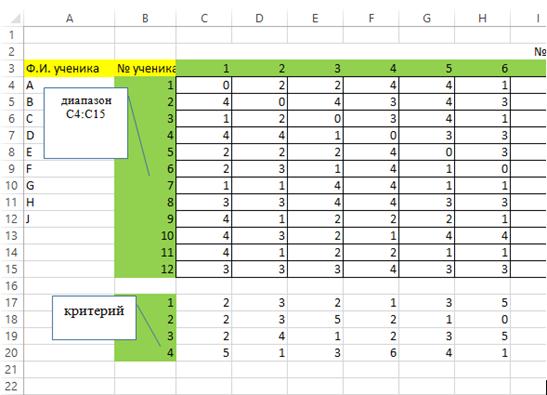 Таблица 4. Результат расчета социального статуса учеников  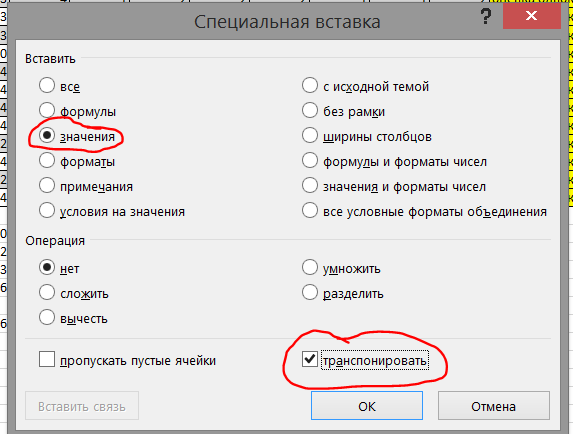 Рис. 24. Диалоговое окно команды Специальная вставка. Перенос данных с транспонированием Вопрос 4. Статистический анализ экспериментальных данных в MS Excel. Статистические методы позволяют психологу обосновывать правильность используемых методик и приемов, обобщать данные эксперимента, находить зависимости между исследуемыми психологическими признаками, выявлять существенные различия между различными группами испытуемых с точки зрения исследуемого признака, строить прогнозы поведения испытуемых, избегать логических и содержательных ошибок при интерпретации полученных данных и т. д. На рынке существует целый ряд приложений анализа данных, включающих и статистически методы. Универсальный пакет для технических вычислений MatLab, имеет собственный язык, позволяющий легко добавлять и модифицировать встроенные компоненты статистического анализа. Широко известен многофункциональный пакет Statistica, популярный в России и благодаря полной русификации. Однако простые задачи статистической обработки можно выполнить и в Excel. Среди встроенных функций MS Excel 2013 имеется группа Статистика, с большим набором возможностей. Расширяет возможности надстройка ПАКЕТ АНАЛИЗА – дополнение Excel, расширяющее аналитические возможности и позволяющее строить гистограммы, делать случайные или периодические выборки данных и находить их статистические характеристики, генерировать неравномерно распределенные случайные числа, проводить регрессионный анализ и многое другое. По умолчанию ПАКЕТ АНАЛИЗА не установлен. Чтобы его установить, нужно открыть диалоговое окно Файл>Параметры. В левой части окна выбрать Надстройки и перейти в новое диалоговое окно. В нижней части окна выбрать Надстройки Excel и нажать кнопку Перейти (Рис. 25). В новом диалоговом окне выбрать опцию Пакет анализа и ОК.  Рис. 25. Окно загрузки надстройки ПАКЕТ АНАЛИЗА Описательная статистика. Описательная статистика позволяет обобщать первичные результаты, полученные при наблюдении или в эксперименте. Процедуры здесь сводятся к группировке данных по их значениям, построению распределения их частот, выявлению центральных тенденций распределения (например, средней арифметической) и, наконец, к оценке разброса данных по отношению к найденной центральной тенденции. Медиана — это элемент выборки, число элементов со значениями больше и меньше которого – равны. Мода — вычисляет количество наиболее часто встречающихся значений в выборке (наиболее вероятная величина). Дисперсия – позволяет оценить дисперсию по выборочным данным —степень разброса элементов выборки относительно среднего значения. Эксцесс – степень выраженности хвостов распределения, т.е. частоты появления величин, удаленных от среднего значения. Асимметрия указывает на отклонение распределения от нормального. Гистограмма геометрическое изображение эмпирической функции плотности вероятности некоторой случайной величины, построенное по выборке. Корреляция (коэффициент линейной корреляции) - позволяет исследовать тесноту связи, т.е. степень разброса точек от линии. Значения, равные 1 или -1 говорят о линейной связи величин, значение 0 – о полной отсутствии связи. Рассмотрим на предыдущем примере распределение оценок учениками своих одноклассников (Таблица 2). а) Данные> Пакет анализа>Описательная статистика. б) В открывшемся диалоговом окне выбираем входные данные столбец с данными ученика 6 (лидер) (Рис. 26). Группирование по столбцам, выходной интервал записываем верхнюю левую ячейку диапазона результата. 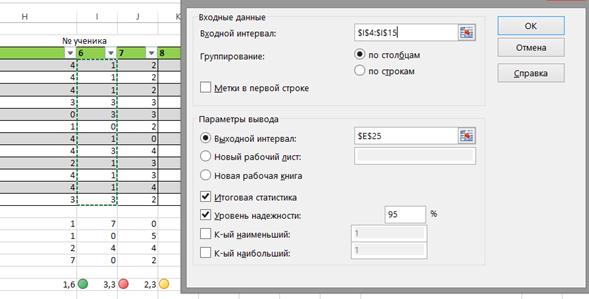 Рис. 26. Ввод данных в диалоговое окно Описательной статистики В таблице 5 показаны результаты первичной статистической обработки данных пакетом Описательная статистика. Как видно из таблицы, чаще всего одноклассники выбирали для лидера вариант «дворец» (1-й выбор): МОДА=1. Сравнив результаты для двух учеников, вы увидите, что оценка лидера имеет значительно меньшую дисперсию (1,17), чем в случае низкого статуса (2,06), т.е. дети почти единогласны в выборе лидера, а остальные статусы выражены менее четко. Таблица 9. Описательная статистика для оценки двух учеников (№ столбца соответствует табл. 10)
Проверка нормальности распределения. При решении практических задач закон распределения случайных величин и его параметры неизвестны. Однако для решения задачи необходимо иметь информацию о том, каков закон распределения и каковы его параметры, т.к. разные распределения имеют разные свойства. В этом случае решают задачу проверки гипотезы. Исходя из предположения (гипотезы), что распределение случайных чисел подчиняется тому или иному закону, выполняют проверку этой гипотезы. Суть задачи проверки соответствия сводится к оценке меры соответствия экспериментальных данных и какого-либо теоретического распределения. Часто методом проверки соответствия теоретическому распределению является использование критерия согласия. Одним из них является критерий согласия хи-квадрат. В Excel проверка согласия по критерию хи-квадрат реализуется функцией ХИ2ТЕСТ. Эта функция вычисляет вероятность совпадения наблюдаемых (фактических) значений и теоретических (гипотетических) значений. Если вычисленная вероятность ниже уровня значимости (а < 0,05), то утверждается, что экспериментальные значения не соответствуют теоретическому распределению. Функция имеет параметры: ХИ2ТЕСТ (фактический интервал; ожидаемый интервал), Для получения правильных результатов необходимо, чтобы объем выборки был не менее 40, выборочные данные сгруппированы в интервальный ряд с количеством интервалов не менее 7, а количество наблюдений в каждом интервале (частот) не менее 5. Пример. Проверка гипотезы о нормальном распределение баллов, полученных при сдаче зачета тестированием. В таблице 10 приведены результаты, полученные из описательной статистики и гистограммы по частотному распределению полученных баллов. Вычислим теоретические частности распределения. Поскольку мы проверяем соответствие заданной совокупности случайных величин нормальному закону распределения, то для расчета применим функцию НОРМРАСП. Установим курсор в ячейку С2 и вызовем из мастера функций функцию нормрасп Заполним поля аргументов: х - А2, среднее - $A$15, стандартное_откл. -$В$15, интегральный – истина. Однако эта функция дает интегральную кривую, а частоты соответствуют кривой плотности распределения. Чтобы получить плотность распределения в С3 вводим =НОРМРАСП(А3; $A$15;$В$15;1)-СУММ($С$2:С2) и копируем ее до конца столбца С (табл. 11). Для вычисления теоретических частот в столбце D умножим значения столбца С на среднее значение (табл. 11). Таблица 10. Обработка распределения баллов, полученных при тестировании 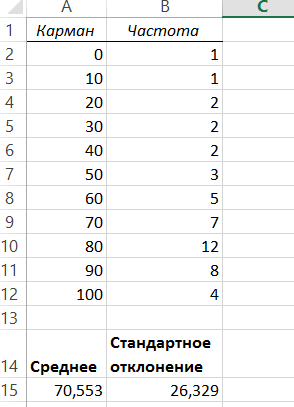 Применяя функцию ХИ2ТЕСТ, определим соответствие данных выборки нормальному закону распределения. Для этого: · установим курсор в свободную ячейку D14; · включим Мастер функций, выберем категорию Статистические, а в списке функций - функцию ХИ2ТЕСТ; · заполним поля аргументов функции: фактический - введем адрес диапазона абсолютных частот B2:B12, ожидаемый -адрес диапазона теоретических частот D2: D12; · после щелчка на кнопке ОК в ячейке D14 будет вычислено значение вероятности того, что выборочные данные соответствуют нормальному закону распределения 0,35833. Для того чтобы отвергнуть нулевую гипотезу о нормальности распределения эта вероятность должна быть меньше уровня значимости α = 0,05, поэтому принимаем гипотезу о нормальности распределения. Таблица 11. Подготовка данных для критерия хи-квадрат 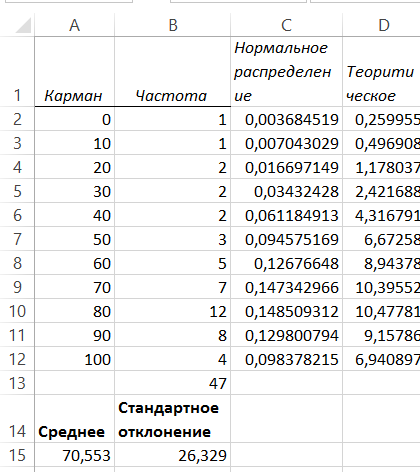 Технологии решения задач корреляционного анализа. Одной из задач статистического моделирования является изучение связи между некоторыми наблюдаемыми переменными. Результаты, полученные при таком исследовании, позволяют прогнозировать развитие ситуации в случае изменения конкретных характеристик изучаемого объекта или процесса. Задача подобного исследования решается методами корреляционного анализа. Под корреляцией понимается взаимосвязь некоторых величин, представленных данными – векторами или матрицами. Общепринятой мерой линейной корреляции является коэффициент корреляции. Его близость к единице указывает на высокую степень линейной зависимости. Если значение корреляции положительно, то связь прямая, при отрицательном значении корреляции – связь обратная, т.е. увеличение одного параметра сопровождается уменьшением второго. Принято считать сильной связью значение абсолютной величины корреляции в пределах от 1 до 0,6 считается высокой, значения в пределах от 0,6 до 0,2 говорят о слабой корреляции, к значениям ниже 0,2 следует относиться с осторожностью. Надо помнить, что наличие корреляции не говорит о наличие причинно-следственной связи между параметрами. Отсутствие тоже может говорить о существовании более сложной зависимости, чем линейная. Целью решения задачи является получение корреляционной матрицы, которая представляет собой симметричную матрицу с единично диагональю. В Excel для целей корреляционного анализа служит инструмент Корреляция, который позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами. Корреляционная матрица – это квадратная таблица, на пересечении соответствующих строк и столбцов которой располагаются корреляционные коэффициенты. Для выполнения корреляционного анализа необходимо выполнить следующую последовательность операций: · выполнить команду меню Данные >Анализ данных; · в списке Инструменты анализа диалогового окна Анализ данных выбрать строку Корреляция; · в раскрывшемся окне диалога Корреляция в поле Входной интервал ввести адресную ссылку на диапазон, содержащий анализируемые данные (входной интервал должен состоять н менее чем из двух столбцов), установить соответствующий переключатель Группировка, установить переключатель Параметр вывода и ввести адрес верхней левой ячейки, с которой будет начинаться диапазон для вывода результатов вычислений; · щелкнуть на кнопке ОК. В результате выполнения вычислений в выходной диапазон буде помещена корреляционная матрица. Пример. Есть статистические данные, регистрирующие количество выходных и праздничных дней в месяце в период с января по июнь и снимаемые со счетов суммы (Табл. 12). Требуется определить, существует ли взаимосвязь между количеством выходных и праздничных дней и величиной сумм, снимаемых со счетов. Таблица 12. Данные для проверки корреляции активности вкладчиков (снятие денег) и количеством выходных в месяце
Решение. Используем Пакет анализа >Корреляция. В диалоговом окне укажем диапазон, в котором расположены числа, опцию По столбцам и диапазон вывода результата. Получим заполненный диапазон (Табл. 13). Как видно из таблицы, корреляция между столбцом 1 и столбцом равна 0,734666. Эта величина больше 0,6, поэтому можно считать, что существует прямая связь между числом выходных и снятием денег. Хотя для малых выборок корреляция становится менее достоверной. Таблица 13. Результат корреляционного анализа
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
