Математические основы криптологии
 Скачать 1.3 Mb. Скачать 1.3 Mb.
|
|
Стойкость криптографических систем и алгоритмов. Информационно - теоретический подход и подход на основе теории сложности. Основным назначением криптосистем является обеспечение передачи секретных сообщений через несекретные каналы связи. Поэтому важнейшей характеристикой любой криптосистемы является ее стойкость, т.е. способность противостоять попыткам дешифровать перехваченный шифротекст или раскрыть ключи шифра. Исторически первым подходом к определению стойкости криптосистем был информационно - теоретический подход, предложенный К. Шенноном. Этот подход основан на понятии информации, ее количественной оценке и анализе количества информации об открытом тексте, для обеспечения стойкости криптосистемы. Формально количество информации в сообщении измеряется энтропией. Пусть 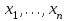 есть n возможных сообщений, появляющихся с вероятностями есть n возможных сообщений, появляющихся с вероятностями Тогда энтропия сообщения x есть 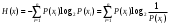 Для заданного n величина H(x) принимает max значение, равное 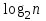 при при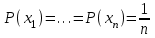 , ,т.е. когда все сообщения равновероятны. Неопределенность (энтропия) уменьшается, когда распределение вероятностей сообщений становится все более отличным от равновероятного и достигает min H(X)=0 когда 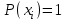 для некоторого сообщения для некоторого сообщения 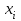 . Энтропия сообщения измеряет его неопределенность в числе бит информации, которая должна быть восстановлена, когда сообщение было скрыто от криптоаналитика в шифротексте. . Энтропия сообщения измеряет его неопределенность в числе бит информации, которая должна быть восстановлена, когда сообщение было скрыто от криптоаналитика в шифротексте.К. Шеннон различал теоретическую и практическую стойкость криптосистем. Криптосистема называется теоретически стойкой, если криптоаналитик не может уточнять распределение вероятностей возможных открытых текстов по имеющемуся и у него шифротексту, даже если он обладает всеми необходимыми для этого средствами. При этом предполагается, что секретный ключ используется только один раз (т.е. сеансовый режим использование ключа). Совершенная секретность означает, что открытый текст М и шифротекст С статистически независимы т.е. совпадают вероятности 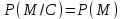 для всех возможных M и C и получение шифротекста не дает криптоаналитику дополнительной информации о посланном открытом тексте. Определение совершенной секретности можно также представить в виде 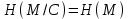 Пусть P(C/M) - условная вероятность получения шифротекста С при условии, что известно, что зашифрован текст М на некотором неизвестном ключе. Тогда 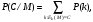 где 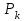 - вероятность использования ключа - вероятность использования ключа 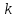 , ,  - преобразование зашифрования на ключе - преобразование зашифрования на ключе 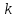 . .Обычно существует по крайней мере один ключ 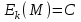 для данных М и С, но иногда текст М может быть зашифрован в текст С при нескольких различных ключах. для данных М и С, но иногда текст М может быть зашифрован в текст С при нескольких различных ключах.Необходимым и достаточным условием для совершенной секретности является то, что для каждого С и для всех М выполнено т.е. вероятности получения конкретного шифра С, при условии что был зашифрован текст М, одинаковы для всех М. Используя то факт, что уменьшение объема известных сведений может лишь увеличить неопределенность, т.е. энтропию, получим 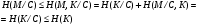 (Здесь естественно 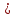 неопределенности шифруемого с его помощью текста отсюда можно сделать вывод, что размер ключа неопределенности шифруемого с его помощью текста отсюда можно сделать вывод, что размер ключа 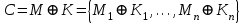 , ,при случайном равновероятном выборе ключа 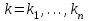 и и 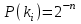 для всех i=1,…,n, откуда для всех i=1,…,n, откуда 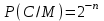 для всех С и М т.е. выполняется условие совершенно секретной системы. для всех С и М т.е. выполняется условие совершенно секретной системы.Помимо теоретической стойкости криптосистемы рассматривают ее практическую стойкость. Для этого вводят рабочую характеристику W(n) - среднее количество работы (измеренное в удобных единицах), требуемое для нахождения ключа 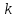 на основе знания n знаков шифротекста с помощью наилучшего криптоаналитического алгоритма. Обычно криптосистемы оценивают с помощью достигнутой оценки рабочей характеристики W( на основе знания n знаков шифротекста с помощью наилучшего криптоаналитического алгоритма. Обычно криптосистемы оценивают с помощью достигнутой оценки рабочей характеристики W(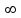 ) при использовании наилучшего из известных методов дешифрования. Криптосистемы называются практически стойкими если они не могут быть вскрыты в течение реального времени ( ) при использовании наилучшего из известных методов дешифрования. Криптосистемы называются практически стойкими если они не могут быть вскрыты в течение реального времени (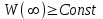 ) всеми общедоступными методами. На практике используют именно это понятие стойкости криптосистем. По сути дела из этого определения можно сделать вывод о том, что проблема создания практически стойких криптосистем или шифров может быть сведена к проблеме нахождения наиболее сложных задач, удовлетворяющих определенным условием. Можно составить шифр таким образом, чтобы раскрытие его было эквивалентно (или включало в себя, решение некоторой задачи, про которую известно, что для ее решения требуется определенный (желательно большой объем) работы). Поэтому стойкость криптосистемы можно определить вычислительной сложностью алгоритмов, применяемых криптоаналитиками для шифрования. Такой подход к определению стойкости криптосистем, основанный на понятии вычислительной сложности криптоаналитических алгоритмов (в отличие от информационно - теоретического, рассмотренного выше) основан не на вопросе о том возможно ли извлечь информацию об открытом тексте из анализа шифротекста, а на вопросе о том, осуществимо ли это в приемлемое время. Этот подход позволяет достичь свойства совершенной секретности криптосистемы даже для случаев, когда используется секретные ключи значительно меньше по размерам чем длина открытого шифруемого текста. ) всеми общедоступными методами. На практике используют именно это понятие стойкости криптосистем. По сути дела из этого определения можно сделать вывод о том, что проблема создания практически стойких криптосистем или шифров может быть сведена к проблеме нахождения наиболее сложных задач, удовлетворяющих определенным условием. Можно составить шифр таким образом, чтобы раскрытие его было эквивалентно (или включало в себя, решение некоторой задачи, про которую известно, что для ее решения требуется определенный (желательно большой объем) работы). Поэтому стойкость криптосистемы можно определить вычислительной сложностью алгоритмов, применяемых криптоаналитиками для шифрования. Такой подход к определению стойкости криптосистем, основанный на понятии вычислительной сложности криптоаналитических алгоритмов (в отличие от информационно - теоретического, рассмотренного выше) основан не на вопросе о том возможно ли извлечь информацию об открытом тексте из анализа шифротекста, а на вопросе о том, осуществимо ли это в приемлемое время. Этот подход позволяет достичь свойства совершенной секретности криптосистемы даже для случаев, когда используется секретные ключи значительно меньше по размерам чем длина открытого шифруемого текста.Вычислительная сложность алгоритма в свою очередь измеряется его временной и емкостной S сложностями в зависимости от размера n входных данных. Временная сложность - это время, затрачиваемое алгоритмом для решения задачи, рассматриваемое как функция размера задачи или количества входных данных. Емкостная сложность - это емкость необходимой машинной памяти. Поведение этих сложностей в пределе при увеличении размера задачи называется асимптотическими сложностями. Эти сложности алгоритма определяют в итоге размер задачи, которую можно решить этим алгоритмом. Если при данном размере задачи в качестве меры сложности берётся наибольшая из сложностей по всем входам этого размера, то она называется сложностью в худшем случае. Если в качестве меры сложности берется «средняя» сложность по всем входам данного размера, то она называется средней сложностью. Обычно среднюю сложность найти труднее чем сложность в худшем случае. Теория сложности в основном имеет дел со сложностью задач в худшем случае. Для анализа работы алгоритма нужны модели вычислительных машин, достаточно точно отражающих основные черты реальных машин. В качестве таких моделей используются машины с произвольным доступом к памяти, машины с произвольным доступом к памяти и хранимой программой, детерминированная и недетерминированная машины Тьюринга и другие. Если алгоритм обрабатывает входы размера n за время = 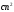 ,где с - const, то говорят что временная сложность этого алгоритма есть ,где с - const, то говорят что временная сложность этого алгоритма есть 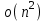 (читается порядка (читается порядка 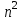 ). Строго в математическом смысле: неотрицательная ). Строго в математическом смысле: неотрицательная 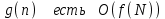 если существуют постоянные с и если существуют постоянные с и 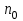 , для которых , для которых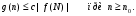 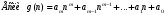 , то , то 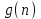 является полиномиальной функцией степени m т.е. является полиномиальной функцией степени m т.е. 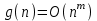 . .Полиномиальным алгоритмом или алгоритмом полиномиальной временной сложности называется алгоритм, у которого временная сложность равна = 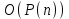 , где Р(n) - некоторый полином, а n - размер задачи (входа). Алгоритмы, временная сложность которых есть =0( , где Р(n) - некоторый полином, а n - размер задачи (входа). Алгоритмы, временная сложность которых есть =0(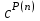 ), где с -const, Р(n) - полином, называется экспоненциальными. ), где с -const, Р(n) - полином, называется экспоненциальными.Для примера в таблице приведены времена для различных классов алгоритмов при 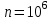 на обычной последовательной ЭВМ с быстродействием на обычной последовательной ЭВМ с быстродействием 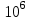 операций в секунду. операций в секунду.
Из таблицы видно, что при =О(n3)выполнение алгоритма становится практически невозможно на последовательной машине. Однако на машине с 106 параллельно работающими процессорами вычисление алгоритма сложностью =О(n3) может занять 10 дней. В тоже время вычисление алгоритма сложностью =О(2n) практически невозможно даже на параллельной машине с одним триллионом процессоров. Задачи, которые решаются за полиномиальное время называются решаемыми, так как они обычно могут быть решены для задач достаточно большой размерности n. Задачи, которые не могут быть систематически решаемыми за полиномиальное время называют нерешаемыми или просто трудными. Существуют и алгоритмически неразрешимые задачи, для которых невозможно создать алгоритм решения. Например, десятая проблема Гильберта: существует ли алгоритм, решающий в целых числах уравнение 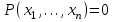 для многочлена Р с целыми коэффициентами. Доказано, что такого алгоритма не существует. На рисунке представлена классификация задач по степени их сложности и дано их возможное наглядное соотношение друг с другом (точно это соотношения не известно). 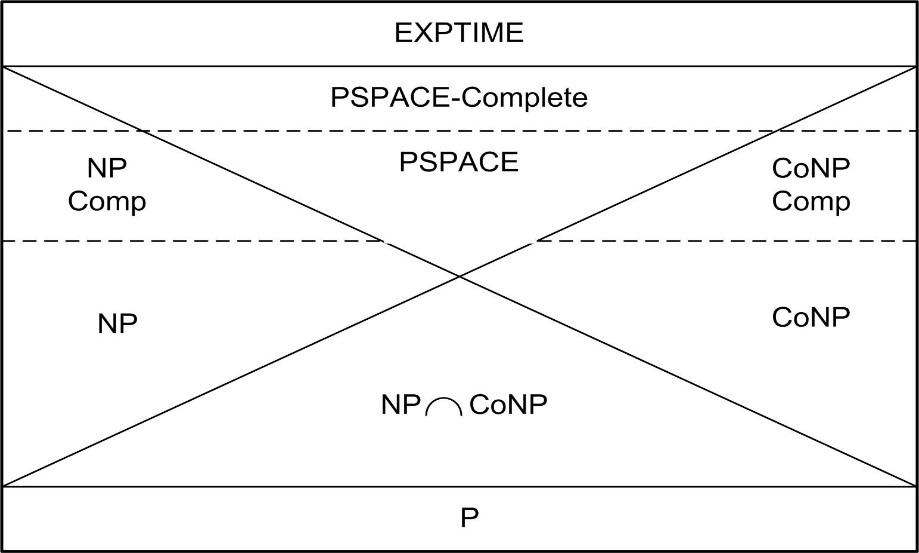 Класс Р или P - TIME состоит из всех задач, решаемых за полиномиальное время. Класс NP или NP - TIME, состоит из всех задач решаемых за полиномиальное время на недетерминированной машине Тьюринга, способной параллельно выполнять неограниченное количество независимых вычислений. Это означает, что если вариант решения проверяется, то он может быть проверен на такой машине Тьюринга за полиномиальное время. Конечно, это не означает решить задачу, так как нет гарантии, что машина проверяет правильно отгаданное решение. Чтобы проверить все варианты решения и найти нужное (т.е. чтобы решить задачу из NP класса), по-видимому, необходимо затратить экспоненциальное время. Примером такой задачи является известная «задача рюкзака»: имеется множество из n целых чисел A=(a1,…,an ) и целое число S. Требуется определить, существует ли подмножество чисел из А такое, чтобы их сумма была бы равна S. Эта задача принадлежит к классу NP задач, так как для любого подмножества чисел из А легко проверить равна ли их сумма S. Найти же такое подмножество чисел, сумма которых равна S гораздо труднее. Существует 2n таких подмножеств и проверка их всех имеет временную сложность =О(2n). Класс NP включает класс P, так как любая задача, полиномиально решаемая на детерминированной машине Тьюринга, может быть полиномиально решена и на недетерминированной машине Тьюринга. Еще никто не доказал, что NP=P также как и то, что 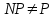 . .Основной метод, используемый для доказательства близости по сложности задач, состоит в сведении задач друг к другу с помощью конструктивного преобразования. Известно много примеров такого преобразования. В 1971 году Кук доказал теорему, согласно которой любая задача о выполнимости имеет свойство, что каждая другая задача из NP класса может быть сведена к ней за полиномиальное время. В тоже время Карп доказал, что многие хорошо известные комбинаторные задачи, включая задачу «о коммивояжере» (выбрать маршрут, посещения разных городов так, чтобы в каждый город попасть только один раз) столь же трудны, как и задача о выполнимости. Класс NP Complete (NP - полных) задач включает все самые трудные NP задачи. Если какая - либо из NP полных задач окажется в классе P, то будет доказано равенство NP=P Класс С0 NP состоит из всех задач, являющихся дополнительными для некоторых задач из NP. Если задача в NP имеет вид: «определить существует - ли решение», то задача из CoNP имеет вид «показать, что решений нет». На сегодняшний день не известно верно - ли равенство CoNP=NP, но есть задачи, принадлежащие пересечению классов CoNP и NP т.е. CoNPNP. Примером такой задачи является «задача о разложении чисел»: дано целое число n, определить существуют - ли делители p и q, такие что n=pq. Эта задача нашла плодотворное применение в криптологии. При этом, задача нахождения делителей p и q сложнее, чем задача установления разложимости числа n (разложимость n можно установить проверкой равенство n=pq при выбранных p и q, что достаточно просто сделать) Класс PSPACE состоит из задач, требующих полиномиальных объемов машинной памяти, но не обязательно решаемых за полиномиальное время. Этот класс включает классы CoNP и NP (CoNP - Complete и NP.Complete), но есть в нем задачи, которые труднее чем CoNP(CoNP - complete) и NP(NP - complete). Класс PSPACE - complete (полных) задач состоит из задач, имеющих свойство, что если какая-нибудь из них окажется принадлежащей классу NP, то NP=PSPACE, или если эта задача окажется в P, то PSPACE=P. Таким образом, выбор наиболее сложных задач, для которых известно решение, и использование их в основе построения криптосистемы, позволяет создавать практически устойчивые шифры, раскрытие которых в принципе возможно, но для этого потребуется столько времени, что эта процедура дешифрования теряет практический смысл. Более подробно об этом речь пойдет на следующих лекциях. Задача выполнимости заключается в проверке существования выполняющего набора булевых переменных V1,…,Van для набора дизъюнкций (операция «или») над этим множеством элементов. |
