Математические основы криптологии
 Скачать 1.3 Mb. Скачать 1.3 Mb.
|
|
3. Элементы теории чисел: основные понятия и теоремы. В дальнейшем изложении будем использовать следующие понятия и обозначения: N - множество натуральных чисел: целые положительные числа вида 1,2,… Z - множество целых чисел: числа вида n, -n и 0, где n - натуральное число. Q - множество рациональных чисел: числа вида p/q, где p и q - целые числа и 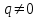 . Класс рациональных чисел включает в себя все целые числа Z, которые в свою очередь включают в себя все натуральные числа N. . Класс рациональных чисел включает в себя все целые числа Z, которые в свою очередь включают в себя все натуральные числа N.R - множество действительных чисел: этот класс включает все рациональные числа и все числа не являющиеся таковыми т.е. все иррациональные числа. Рассмотрим множество целых чисел, которые обозначим через Z. На множестве целых чисел рассмотрим операции сложения + и умножения 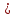 . Операция деления, обратная операции умножения, выполняется не для всех пар чисел из Z. (Напомним Z - целые числа). . Операция деления, обратная операции умножения, выполняется не для всех пар чисел из Z. (Напомним Z - целые числа). Число а делится на число b 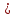 0, если существует число q такое, что 0, если существует число q такое, что 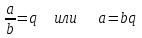 В этом случае говорят, что число b делит число a. При этом число b - делитель числа а, число а - кратное числа b, число q - частное от деления а на b. Число 0 делится на любое целое 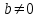 . Если . Если 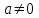 , то очевидно, что множество всех делителей числа а конечно. , то очевидно, что множество всех делителей числа а конечно.Утверждение о том, что b делит а обозначают символом 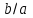 . Если b не делит а, то этот факт обозначают . Если b не делит а, то этот факт обозначают 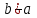 . .Лемма 1. Если 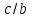 и и 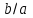 , то , то 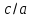 . .Доказательство: по определению из 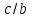 и и 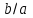 имеем, что b=q1c, a=q2b, откуда а=q1q2c=qc и снова по определению имеем, что b=q1c, a=q2b, откуда а=q1q2c=qc и снова по определению 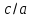 . .Лемма 2. Если m=a+b, d/m и d/a, то d/a. Доказательство: по определению m=q1d и a=q2d. Поэтому из равенства m=a+b получим b=q1d - q2d=(q1 -q2)d=qd, откуда следует d/b. Отсюда следует, что если m=a1+a2+…+an -1+an и d делит числа m, а1,…,аn -1, то d/an. Общим делителем двух или нескольких чисел называется число, являющееся делителем каждого из этих чисел. Если а1,…,аnчисла из Z и хотя бы одно из них не равно нулю, то множество их общих делителей конечно и среди этих делителей существует наибольшее число. Наибольшим общий делителем (НОД) чисел а1,…,аnназывается наибольший из их общих делителей. Он обозначается (а1,…,аn). Число n>1 называется простым, если оно не имеет других делителей кроме 1 и n. Например, числа 2, 3, 5, 7 являются простыми, т.к. они делятся только на 1 и на самих себя. Число n называется составным, если оно имеет делитель отличный от 1 и n. Например, числа 4, 6, 8 составные числа. Если НОД (а1,…,аn)=1, то числа а1,…,аn называют взаимно простыми Например: (2,5)=1; (10,21)=1 Лемма 3. Если a, b, c - целые числа, то (a, b)=1 b/ac, то b/c. Лемма 4. Если целое число b взаимно просто с каждым из целых чисел а1,…,аn, то b взаимно просто с их произведением а1а2,…, аn Когда а не делится на b, то принято говорить о делении а на b с остатком r. Теорема о делении с остатком. Если а и b целые числа, то b>0, то существуют единственные целые числа q и r такие, что a=b*q+r, 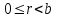 . .Число q называют неполным частным при делении a на b, число r называют остатком от деления а на b. Очевидно, что если r=0, то b/a. Пример. Пусть b=12… Тогда для чисел а= 110, а= -53, а =156 имеем а=b  q+r q+r110=12  9+2 0<r=2<b=12 9+2 0<r=2<b=12-53=12+(-5)+7 0<r=7<b=12 156=12  13 +0 r=0 13 +0 r=0Любое натуральное составное число n представляется в виде n=ab, 1<a<n, 1 Лемма 5. Наименьший отличный от единицы делитель натурального числа n>1 есть простое число. Доказательство. Число n>1 имеет хотя бы два различных делителя (1 и n) и, следовательно, имеет делитель отличный от единицы. Среди всех делителей отличных от 1 имеется наименьший. Пусть это будет q. Число q должно быть простым т.к. в противном случае оно было бы составным и по определению имело бы делитель q1 такой, что 1<q1<q. Но q1/q и q/n, а тогда по лемме1 q1/n. Это противоречит тому, что q наименьший делитель n, значит q - простое число. Следствие. Каждое натуральное число n>1 имеет хотя бы один простой делитель. Лемма 6. Наименьший простой делитель составного числа n не превосходит 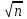 . .Доказательство. Пусть p>1 наименьший делитель числа n являющийся по лемме 5 простым числом. Так как n составное число, то n=pq, где 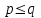 . Поэтому . Поэтому 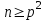 ,откуда ,откуда 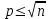 . .Лемма 7. Если p - простое число, то любое целое число а либо взаимно простое с р, либо делится на р т.е. р/а. Доказательство. Наибольшим общим делителем (а, р) чисел а и р может быть только делитель простого числа р, который в свою очередь может быть равен 1 или р. тогда в первом случае (а, р)=1 и числа а и р взаимно простые, а во втором случае когда (а, р)=р а делится на р т.е. р/а. Основная теорема арифметики. Любое натуральное число n>1 представляется в виде произведения простых чисел, причем единственным образом. Доказательство. По лемме 5 число n>1 имеет наименьший простой делитель р1. тогда n=p1a1. Если а1>1, то аналогично получим а1=р2а2, где р2 наименьший простой делитель числа а1>1. Т.к. числа а1, а2,… убывают, то на некотором r шаге будем иметь ar -1=pr ar где ar =1 т.е. ar -1=pr. Перемножая все полученные таким образом равенства после сокращения на а1, а2,…ar -1 получим разложение числа n на простые сомножители n= p1  p2 p2 … … pr prПусть n>1 и оно представлено в виде разложения на простые сомножители n= p1  p2 p2 … … pr prСреди чисел p1,…,pr могут быть одинаковые. Пусть p1,…,pк различные из чисел p1,…,pr (r>k), a 1,…,k кратности с которыми они входят в исходное разложение. Тогда это разложение можно записать в виде: 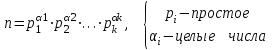 , ,который называется каноническим разложением числа n на простые множители. Пример 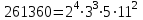 . .Согласно теореме Евклида: Множество простых чисел бесконечно. Для того, чтобы составить таблицу всех простых чисел можно использовать метод, называемый решетом Эратосфена (древне - греческий математик). Напишем одно за другим числа 2,3,…N Число 2 является простым оставляем и зачеркиваем после него все числа кратные 2 т.е. все четные числа. Следующим за числом 2 является число 3, которое является простым. Оставляем 3, зачеркиваем все числа кратные 3. Продолжая этот процесс, находим все простые числа, не превышающие заданного числа N. Например, N=40: 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 Простые числа: 2,3,5,7,11,13,17,19,23,29,31,37 Построение в настоящие время таблицы простых чисел показывают, что с ростом их величин они встречаются все реже и реже. Например, в первой сотне чисел (N=100) их 25, во второй - 21, третьей 16 и т.д. В первой 1000 их 168, во второй тысяче - 135, в третьей - 120 и т.д. Особый класс простых чисел составляют числа вида 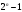 . Такие числа называют простыми числами Мерсенна и они являются наибольшими по своему размеру среди других известных простых чисел. Во времена Эйлера наибольшим простым числом было пятое число Мерсенна 231-1. Через сто лет было найдено шестое число Мерсенна 261-1. В 1992 найдено самое большое известное число -32 число Мерсенна. Его запись содержит 227 832 цифры и требует около ста страниц текста. . Такие числа называют простыми числами Мерсенна и они являются наибольшими по своему размеру среди других известных простых чисел. Во времена Эйлера наибольшим простым числом было пятое число Мерсенна 231-1. Через сто лет было найдено шестое число Мерсенна 261-1. В 1992 найдено самое большое известное число -32 число Мерсенна. Его запись содержит 227 832 цифры и требует около ста страниц текста.Простые числа распределены в натуральном ряде чисел очень нерегулярно. Согласно основной теоремы арифметики, простые числа являются теми простейшими объектами, из которых с помощью умножения строятся все натуральные числа большой единицы. Поэтому вопросы, связанные с распределением простых чисел являются важнейшими в теории чисел. Для того была введена функция П(х) выражающая число простых чисел 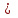 х. Известно, например, что П(1)=0, П(2)=1, П(10)=4, П(40)=12… . Однако для функции П(х) неизвестно никакой простой формулы, позволила бы изучать её поведение. Существуют определенные оценки для функции П(х) (оценки Чебышева, теоремы об асимптотическом законе распределении простых чисел Римана и другие). По мере необходимости в дальнейшем мы будем использовать эти результаты. Наряду с этим в теории чисел уделяется большое внимание решению аддитивных задач, связанных с возможностью предоставления натуральных чисел в виде суммы простых чисел. Наиболее известная из таких задач - проблема Гольдбаха (1742 г.). Гольдбах в письме к Л. Эйлеру высказал предположение, что всякое нечётное число большее 6 можно представить в виде суммы трех простых чисел. Эйлер в свою очередь высказал более сильную гипотезу: всякое число, начинающееся с 4 можно представить в виде суммы двух простых чисел. Первым результатом, связанным с этой проблемой была теорема о том, что существует постоянная к такая, что каждое натуральное число большее единицы есть сумма не более чем к простых чисел. Далее была доказана теорема (Виноградов И.М.), утверждающая что всякое достаточно большое нечетное число представимо в виде суммы трех простых чисел. х. Известно, например, что П(1)=0, П(2)=1, П(10)=4, П(40)=12… . Однако для функции П(х) неизвестно никакой простой формулы, позволила бы изучать её поведение. Существуют определенные оценки для функции П(х) (оценки Чебышева, теоремы об асимптотическом законе распределении простых чисел Римана и другие). По мере необходимости в дальнейшем мы будем использовать эти результаты. Наряду с этим в теории чисел уделяется большое внимание решению аддитивных задач, связанных с возможностью предоставления натуральных чисел в виде суммы простых чисел. Наиболее известная из таких задач - проблема Гольдбаха (1742 г.). Гольдбах в письме к Л. Эйлеру высказал предположение, что всякое нечётное число большее 6 можно представить в виде суммы трех простых чисел. Эйлер в свою очередь высказал более сильную гипотезу: всякое число, начинающееся с 4 можно представить в виде суммы двух простых чисел. Первым результатом, связанным с этой проблемой была теорема о том, что существует постоянная к такая, что каждое натуральное число большее единицы есть сумма не более чем к простых чисел. Далее была доказана теорема (Виноградов И.М.), утверждающая что всякое достаточно большое нечетное число представимо в виде суммы трех простых чисел.Утверждение о представлении четных чисел в виде суммы двух простых чисел до сегодняшнего дня не доказано. Продолжим знакомство с основными понятиями и теоремами теории чисел, которые будут необходимы для дальнейшего изложения лекционного курса. Пусть mN - натуральные числа. Целые числа а и b (a,bz) называются сравнимыми по модулю mN (m0) если разность a и b делится на m т.е. m/a-b. Сравнимость чисел a и b по модулю m обозначают символом 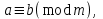 называемым сравнением по модулю m. Числа a и b сравнимы по модулю m тогда и только тогда, когда существует целое t(tz) такое, что 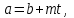 также и только тогда, когда они имеют одинаковые остатки при делении на m т.е. также и только тогда, когда они имеют одинаковые остатки при делении на m т.е.  Отсюда следует, что все целые числа Z по модулю m разбиваются по m непересекающихся классов сравнимых между собой чисел (т.е. имеющих одинаковые остатки при делении на m) Каждое число b, входящее в какой - либо из классов, называется вычетом числа a по модулю m, а каждый класс - классом вычетов по модулю m. Число разных классов вычетов равно m. Полной системой вычетов (по модулю m) называют множество из m целых чисел { 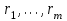 }, если для любого целого числа a существует точно одно число }, если для любого целого числа a существует точно одно число 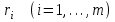 из множества из множества 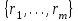 такое, что такое, что 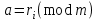 . .Пример: множество {0,1,2,…m -1} Сравнимость по модулю m для произвольных целых, чисел является отношением эквивалентности, (т.е. классы вычетов по модулю m являются классами эквивалентности) т.к. для них справедливо выполнение соотношений: 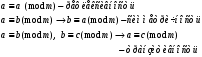 Свойства сравнений по модулю m напоминают свойства обычных числовых равенств: 1. Два числа, сравнимые с третьим, сравнимыми между собой 2. Сравнения по одному и тому - же модулю можно почленно складывать: 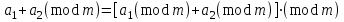 Сравнения по одному и тому - же модулю можно почленно перемножать: 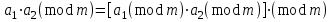 Правила сокращения сравнений несколько отличаются от правил сокращения неравенств. Если 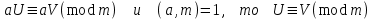 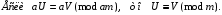 Для каждого целого числа m, m>1 ввести числовую функцию (m), представляющую собой количество чисел из совокупности чисел 0,1,…,m -1 взаимно простых с m. Функцию (m) называют функцией Эйлера. Например: (2)=1, (3)=2, (4)=2, (5)=4, (6)=2 и т.д. Очевидно, что если m=p - простое число, то(p)=p-1. Название функции (m) происходит из следующей теоремы Эйлера: Для любых целых чисел а и m, таких, что (a,m)=1 (т.е. a и m взаимно простые числа) справедливо выражение 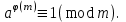 Из теоремы Эйлера следует малая теорема Ферма: Если р - простое число и 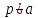 , то , то 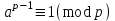 . Это утверждение очевидно, если вспомнить, что для простого числа р, . Это утверждение очевидно, если вспомнить, что для простого числа р, 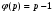 .Наименьшие из чисел .Наименьшие из чисел 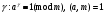 называется показателем числа а по модулю m. Существование таких чисел называется показателем числа а по модулю m. Существование таких чисел 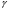 обеспечивается указанной выше теоремой Эйлера. Если показатель числа а по модулю m равен обеспечивается указанной выше теоремой Эйлера. Если показатель числа а по модулю m равен 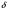 , то , то 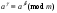 тогда и только тогда, когда тогда и только тогда, когда 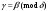 . Показатель числа а по модулю m является делителем числа . Показатель числа а по модулю m является делителем числа 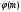 . Если показатель числа aпо модулю m равен . Если показатель числа aпо модулю m равен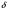 , то показатель числа ak равен , то показатель числа ak равен 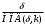 для произвольного целого k. В частном случае, когда показатель числа а по модулю m равен (m), то а называется первообразным (примитивным) корнем по модулю m. Если р – простое число, и число а является первообразным корнем по модулю Р, то любой элемент b из множества чисел 1,2,…,р -1 имеет однозначное представление в виде для произвольного целого k. В частном случае, когда показатель числа а по модулю m равен (m), то а называется первообразным (примитивным) корнем по модулю m. Если р – простое число, и число а является первообразным корнем по модулю Р, то любой элемент b из множества чисел 1,2,…,р -1 имеет однозначное представление в виде 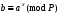 для некоторого целого числа х для некоторого целого числа х {0,1,…,р -1}. {0,1,…,р -1}.Число х при этом называется дискретным логарифмом (или индексом) числа b по основанию а. Сложность вычисления дискретных логарифмов совпадает со сложностью нахождения разложения целого числа на простые сомножители и имеют exp сложность, что определяет широкое применение таких задач при построении современных криптосистем Число m называется псевдослучайным по основанию а, если 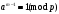 и и 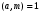 (р – простое число). Существуют составные числа m, являющиеся псевдослучайными для всех а, взаимно простых с m. Такие числа называются числами Кармайкла. Например, (р – простое число). Существуют составные числа m, являющиеся псевдослучайными для всех а, взаимно простых с m. Такие числа называются числами Кармайкла. Например, 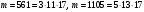 . Если t различных оснований а1,…,аtвыбираются независимо и случайно, то составное число m выдержит тест Ферма . Если t различных оснований а1,…,аtвыбираются независимо и случайно, то составное число m выдержит тест Ферма 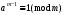 i=1,…,tс вероятностью i=1,…,tс вероятностью 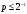 . .Важное значение в теории чисел и для дальнейшего изложения материалов лекционного курса имеет понятие многочлена или полинома. Многочленом называется выражение вида 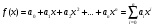 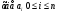 - коэффициенты; - коэффициенты;х – переменная; n - степень многочлена, обозначаемая degf(x). Для многочленов, также как и для чисел, могут быть введены арифметические операции. Два многочлена 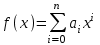 и и 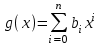 равны тогда и только тогда, когда равны тогда и только тогда, когда 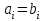 . .Сумма многочленов f(x) и g(x) определяется равенством 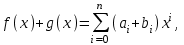 а произведение 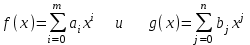 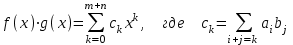 . .Теорема. Пусть f(x) и g(x) многочлены, тогда 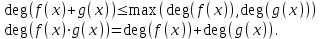 . .Многочлен f(х) делится на многочлен g(x), если существует многочлен q(x) такой, что f(x)=q(x)g(x). В этом случае говорят, что многочлен g(x) делит многочлен f(x), при этом g(x) - делитель многочлена f(x), а f(x) - кратное многочлена g(x). Для многочлена f(x)=a0+a1x+…+anxn коэффициент а0 является постоянным членом т.е. константой. Многочлены степени 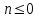 называются постоянными многочленами - константами. называются постоянными многочленами - константами.Теорема (алгоритм деления многочленов с остатком) Пусть g(x)0 некоторый многочлен. Тогда для каждого многочлена f(x) существует также многочлены q(x) и r(x), что 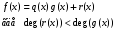 Пример: 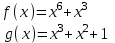 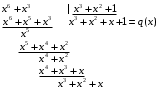 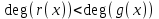 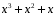 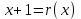 Пусть f(х) – многочлен с целыми коэффициентами. Сравнение вида f(х)0(mod m) называется сравнением с неизвестной величиной. Задача о решении сравнения с неизвестной величиной состоит в отыскании всех значений х, которые ему удовлетворяют. Простейшее линейное сравнение имеет вид axb(mod m), (a,m)=1. Теорема. Пусть d=НОД(a,m). Если d/b, то сравнение axb(mod m) будет иметь d решений вида: 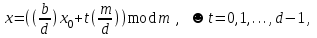 где 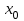 - решение сравнения - решение сравнения 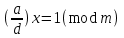 . Если . Если 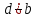 , то решений нет. , то решений нет.Пусть 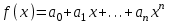 - многочлен с целыми коэффициентами - многочлен с целыми коэффициентами  Два решения Два решения  сравнения n -ой степени сравнения n -ой степени 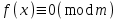 называются эквивалентными, если называются эквивалентными, если 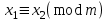 . Числа решений сравнения определяется числом неэквивалентных решений. . Числа решений сравнения определяется числом неэквивалентных решений.Теорема. Пусть  - попарно взаимно простые числа (т.е. НОД( - попарно взаимно простые числа (т.е. НОД(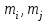 )=1 для )=1 для  ) и ) и 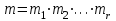 . Тогда справедливо: . Тогда справедливо:1.Сравнение  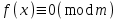 равносильно системе сравнений равносильно системе сравнений 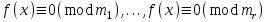 2.Число решений сравнения 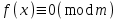 равно произведению числа решений отдельных сравнений указанной в п.1. системы сравнений. равно произведению числа решений отдельных сравнений указанной в п.1. системы сравнений.По аналогии с целыми числами можно ввести понятия наибольшего общего делителя многочленов, наименьшего общего кратного многочленов, взаимно простых и попарно взаимно простых многочленов, отношение сравнимости многочленов и ряд других важнейших понятий. Теорема. 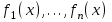 - многочлены, не все равные нулю. Тогда существует однозначно определенный нормативный многочлен d(x), обладающий свойствами - многочлены, не все равные нулю. Тогда существует однозначно определенный нормативный многочлен d(x), обладающий свойствами1.d(x) делит каждый многочлен 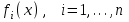 . .2.Любой многочлен g(x), который делит каждый из многочленов 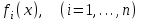 , делит и многочлен d(x). , делит и многочлен d(x).Нормированный многочлен d(x) называют наибольшим общим делителем многочленов 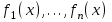 и обозначают НОД( и обозначают НОД(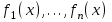 ). Если НОД( ). Если НОД(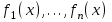 )=1, то многочлены )=1, то многочлены 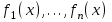 называются взаимно простыми. Они называются попарно взаимно простыми, если называются взаимно простыми. Они называются попарно взаимно простыми, если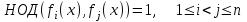 . .Наибольший общий делитель двух многочленов (также как и двух целых чисел) можно найти при помощи алгоритма Евклида. Пусть многочлен g(x)0 и не делит многочлен f(x). Тогда, применяя многократно алгоритм деления многочленов с остатком, получим 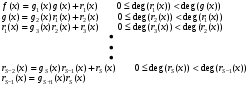 Т.к. степень deg(g(x)) конечна, то процедура заканчивается за конечное число шагов. Если старший коэффициент последнего ненулевого остатка 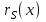 равен b, то равен b, то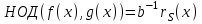 . .Если у нас более чем 2 многочлена (n>2), то НОД( 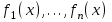 ) при ненулевых многочленах ) при ненулевых многочленах 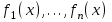 находят (как и для целых чисел), применяя расширенный алгоритм Евклида: сначала определяют НОД( находят (как и для целых чисел), применяя расширенный алгоритм Евклида: сначала определяют НОД( ), а затем находят последовательно, применяя алгоритм Евклида, ), а затем находят последовательно, применяя алгоритм Евклида,НОД(НОД( 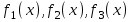 ))=НОД( ))=НОД(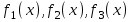 ) и т.д. ) и т.д.Пример: 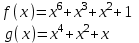 Найдем НОД( 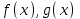 ) по алгоритму Евклида ) по алгоритму Евклида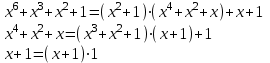 Значит, НОД( 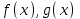 )=1 т.е. многочлены f(x) и g(x) взаимно простые. )=1 т.е. многочлены f(x) и g(x) взаимно простые.Двойственным к понятию НОД является понятие наименьшего общего кратного. Пусть 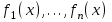 - ненулевые многочлены. Тогда можно показать, что существует однозначно определенный нормированный многочлен m(x), обладающий следующими свойствами: - ненулевые многочлены. Тогда можно показать, что существует однозначно определенный нормированный многочлен m(x), обладающий следующими свойствами:1. m(x) делится на каждый многочлен 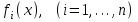 ; ;2. любой многочлен g(x), который делится на каждый из многочленов 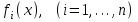 делится на m(x). делится на m(x).Многочлен m(x) называют наименьшим общим кратным многочленов 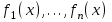 и обозначается НОК и обозначается НОК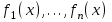 . Для двух многочленов . Для двух многочленов 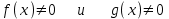 имеет место соотношение имеет место соотношение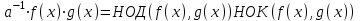 , ,где а - старший коэффициент произведения f(x) и g(x). Важнейшим понятием теории чисел является понятие неприводимого многочлена. Многочлен f(x) называется неприводимым, если он имеет положительную степень и равенство f(x)=g(x)h(x) может выполняться лишь в том случае, когда либо g(x), либо h(x) является постоянным многочленом (т.е. его степень   ). Другими словами, многочлен f(x) является неприводимым, если он допускает только тривиальные разложения на множители. ). Другими словами, многочлен f(x) является неприводимым, если он допускает только тривиальные разложения на множители.Многочлен положительной степени f(x) называется приводимым, если существуют два многочлена положительной степени 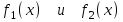 такие, что такие, что 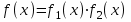 , т.е. если этот многочлен f(x) не является неприводимым. , т.е. если этот многочлен f(x) не является неприводимым.Неприводимые многочлены играют важную роль в теории чисел, так как любой многочлен f(x) может быть записан, причем единственным способом, в виде произведения неприводимых многочленов (аналог того, что любое число n>1 может быть представлено в виде произведения простых чисел). Лемма: Если неприводимый многочлен f(x) делит произведение многочленов 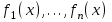 , то по крайней мере один из сомножителей , то по крайней мере один из сомножителей 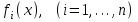 делится на f(x). делится на f(x).Используя эту лемму, можно сделать следующее фундаментальное утверждение: Теорема. (об однозначном разложении на множители) Каждый многочлен положительной степени f(x) может быть представлен в виде произведения 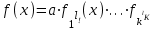 , ,где а старший коэффициент f(x); 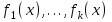 - различные нормированные неприводимые многочлены; - различные нормированные неприводимые многочлены; 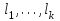 - натуральные числа 1,2,…. - натуральные числа 1,2,….При этом такое разложение называют каноническим разложением многочлена. Наиболее интересные и важные свойства объектов (чисел, многочленов и др.) теории чисел, которые потребуются в дальнейшим, получены и описаны, в частности, в рамках теории конечно поля. Поэтому в дальнейшем рассмотрим элементы теории конечного поля. 4. Элементы конечного поля. Основные понятия и свойства алгебраических структур. |
