Математические основы криптологии
 Скачать 1.3 Mb. Скачать 1.3 Mb.
|
|
Определение. Пусть многочлен f(х1,...,хn) R[x1,...,xn] задан выражением f(x1,...,xn)= 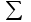 ai1...inx1i1...xnin. ai1...inx1i1...xnin.Если ai1...in0,то ai1...inx1i1...xnin называется членом многочлена f(x1,...,xn), а i1+...+in - степенью этого члена. Степень многочлена f(x1,...,xn) (deg(f)) определяется как наибольшая из степеней его членов. Для f(x1,...,xn)=0 полагают deg(f)= -. Если f(x1,...,xn)=0 и все члены f имеют одну и туже степень, то многочлен f называют однородным. Определение. Многочлен f(x1,...,xn) R[x1,...,xn] называется симметрическим, если для любой перестановки i1+...+in целых чисел 1,...,n выполняется равенство f(xi1,...,xin)= f(x1,...,xn). Введем несколько понятий, связанных с расширением полей, о котором мы немного говорили ранее. Пусть F поле. Подмножество К поля F, которое само является полем относительно операций поля F, называется его подполем. В этом случае поле F называется расширением поля К. Если KF, то К – собственное подполе поля F. Если К - подполе конечного поля Fp при простом Р, то оно должно по определению содержать элементы 0 и 1, а значит, и все другие элементы поля Fp в силу замкнутости поля К по сложению. Следовательно, поле Fp не имеет собственных подполей, отсюда следующее определение: поле, не содержащее собственных подполей называется простым полем. Любое конечное полеFp порядка Р при простом Р есть простое поле. Определение. Пусть К - подполе поля F и М – любое подмножество поля F. Тогда поле К(М) определим как пересечение всех подполей поля F, содержащих одновременно К и М: оно называется расширением поля К, полученным присоединением элементов множества М. В случае конечного множества М={1,...,n} будем писать К(М)=К(1,...,n). Если М состоит из одного элемента F, то поле L=K() называют простым расширением поля К, а элемент F - образующим элементом простого расширения L поля К. Определение. Пусть К – некоторое подполе поля F и F. Если удовлетворяет нетривиальному полиномиальному уравнению с коэффициентами из поля К, т.е. если ann+...+a1+a0=0, где элементы ai лежат в К и не равны нулю одновременно, то элемент называется алгебраическим над К. Расширение L поля К называется алгебраическим расширением поля К, если каждый элемент поля L является алгебраическим над К. Одним из наиболее фундаментальных результатов, относящимся к понятию расширения полей является теорема Кронежра: Пусть многочлен f(x) K[x]неприводим над полем К. Тогда существует простое алгебраическое расширение поля К, образующим элементом которого является некоторый корень f(x). Эта теорема гарантирует для любого неприводимого над полем F существование такого расширения поля F, в котором этот многочлен имеет корень. Рассмотрим теперь вопросы строения конечных полей, опишем их основные свойства и методы построения. 6. Элементы теории конечного поля. Строение конечных полей. Основные свойства и методы построения конечных полей. Из предыдущих лекций вспомним, что для каждого простого числа Р фактор кольцо Z/(р) является конечным полем, состоящим из Р элементов, которое отождествляют с конечным полем Галуа Fр или GF(p) порядка р. Эти поля играют важную роль в теории полей, так как каждое поле характеристики р должно содержать изоморфное Fр подполе и потому может рассматриваться как расширение поля Fр. Рассмотрим вопрос о числе элементов конечного поля. Лемма 1. Пусть F - конечное поле, содержащее подполе К из q элементов. Тогда F состоит из qm элементов, где m=[F:K]. Здесь [F:K] обозначает степень поля F над К, т.е. размерность пространства F над К. Если рассматривать F как векторное пространство над полем К. Теорема. Пусть F - конечное поле. Тогда оно состоит из рn элементов, где р простое число, являющееся характеристикой поля F, а n - натуральное число, являющееся степенью поля F над его простым подполем. Доказательство этой теоремы достаточно простое и приводится, чтобы вспомнить материал прошлой лекции. Так как поле F конечно, то его характеристика есть некоторое простое число р. Поэтому простое подполе К поля F изоморфно Fр и значит содержит р элементов и, следовательно, согласно лемме 1, поле F содержит рn элементов. Лемма 2. Если F - конечное поле из q элементов, то каждый элемент аF удовлетворяет равенству аq=а. Лемма 3. Если F - конечное поле из q элементов и К - подполе поля F, то многочлен xq -x из К[х] вполне разлагается в F[х] следующим образом xq -x=(х -а), аF, так что F является полем разложения многочлена xq -x над полем К. На основе представленных лемм можно сформировать главную характеризационную теорему конечных полей. Теорема о существовании и единственности конечных полей. Для каждого простого числа р и каждого натурального числа n существует конечное поле из рn элементов. Любое конечное поле из q=рn элементов изоморфно полю разложения xq -x над полем Fp. Эта теорема позволяет ввести в рассмотрение т.е. построить конкретное конечное поле Галуа порядка q, содержащее q элементов, где q - это степень простого числа р, которое является характеристикой этого поля. Поля этого типа обозначают Fq или GF(q). Для конечного поля F(q) будем обозначать через F*(q) мультипликативную группу его ненулевых элементов. Тогда следующая теорема устанавливает важное свойство такой группы. Теорема. Мультипликативная группа F*(q) ненулевых элементов произвольного конечного поля Fq является циклической, с образующим элементом b Fq. Определение. Образующий элемент b Fq циклической группы F*q называется примитивным элементом поля Fq. Теорема. Пусть Fq – конечное поле и Fr его конечное расширение. Тогда Fr является простым алгебраическим расширением поля Fq, причем образующим элементом этого простого расширения может служить любой примитивный элемент поля Fr. Отсюда имеет место важное следствие: Для каждого конечного поля Fq и каждого натурального числа n в кольце Fq[x] существует неприводимый многочлен f(x) степени n. Рассмотрим теперь вопрос о множестве корней неприводимого многочлена над конечным полем. На этот важный вопрос дают ответ следующие теоремы конечного поля. Лемма. Пусть f(x) Fq[x] - неприводимый многочлен степени m над Fq. Тогда f(x) делит многочлен 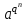 -x тогда и только тогда, когда число m делит n (т.е. m/n). -x тогда и только тогда, когда число m делит n (т.е. m/n).Теорема Галуа. Если f(x) Fq[x] неприводимый многочлен степени m, то в поле Fqm содержится любой корень, а многочлена f(x). Более того, все корни многочлена f(x) просты (напомним, что корень простой, если его кратность к=1) и ими являются m различных элементов 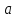 , , 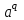 , , 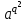 ,..., ,...,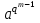 поля Fqm. поля Fqm.Из этой теоремы следуют следующие факты: Неприводимый многочлен f(x) Fq[x] над полем Fqm вполне разлагается в этом поле, т.е. (см. лемму 3). Поле Fqm является полем разложения над полем Fq. Поля разложения любых двух неприводимых многочленов одной и той же степени из кольца Fq[x] изоморфны. Каждое конечное расширение Fqm конечного поля Fq является нормальным расширением, т.е. оно обладает тем свойством, что каждый неприводимый многочлен из Fq[x], имеющий хотя бы один корень в поле Fqm, разлагается в этом поле на линейные сомножители. Любое конечное поле является совершенным полем, т.е. обладает следующим свойством: каждый неприводимый многочлен над этим полем имеет лишь простые корни. Определим теперь ряд понятий, которые потребуются для дальнейшего изучения основных элементов теории конечного поля. Определение.Пусть Fqm расширение поля Fq , и пусть аFqm. Тогда элементы 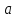 , , 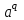 , , 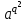 ,..., ,...,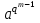 называются сопряженными с элементом называются сопряженными с элементом 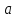 относительно Fq. относительно Fq.Пусть К=Fq, Fq= Fqm (т.е конечное расширение F конечного поля K это векторное пространство над K). Тогда размерность F над K равна m, и если {a1, ..., am } базис пространства F над полем K или базис поля F над K, то каждый элемент aF однозначно представим в виде линейной комбинации a=c1a1+...+ cmam, cjK, 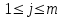 . .Тогда можно ввести важную функция из F в K, которая также является линейной. Определение. Пусть K=Fq, F=Fqm и aF. Тогда определим след 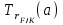 элемента a над равенством элемента a над равенством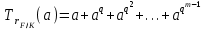 . .Если K простое подполе поля F, то 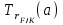 называют абсолютным следом элемента a и обозначают называют абсолютным следом элемента a и обозначают 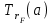 . .Иными словами след 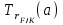 элемента а над полем K есть сумма всех сопряженных с а относительно K элементов. элемента а над полем K есть сумма всех сопряженных с а относительно K элементов.Дадим еще одноопределение следа. Пусть f(x)K[x] минимальный многочлен элемента aF над полем K. Его степень d является делителем числа m. Назовем многочлен g(x)=f(x)m/d из K[x] характеристическим многочленом элемента а над полем К. Согласно представленной выше теореме Галуа корнями многочлена f(x) в поле F являются элементы 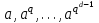 , поэтому получаем, что корнями многочлена g(x) в поле F являются элементы, которые сопряжены с элементом а относительно поля K. Отсюда , поэтому получаем, что корнями многочлена g(x) в поле F являются элементы, которые сопряжены с элементом а относительно поля K. Отсюда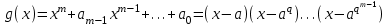 и сравнение коэффициентов дает 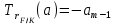 . .Этот след всегда является элементом поля К. Определение. Для aF=Fqm и K=Fq определим норму NF/K(a) элемента а над полем К равенством 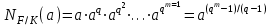 . .Через свободный член 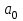 характеристического многочлена элемента а над полем К: характеристического многочлена элемента а над полем К: 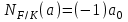 . .Определение.Пусть К конечное поле и F его конечное расширение. Тогда два базиса {a1,...,am} и {b1,...,bm} поля F над К называется дуальными, если для 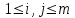 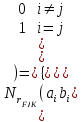 . .Определение. Пусть K=Fq и F=Fqm. Тогда базис поля F над К вида 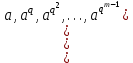 состоящий из подходящим образом выбранного элемента aF и сопряженных с ним относительно поля К элементов, называют нормальным базисом поля F над К. состоящий из подходящим образом выбранного элемента aF и сопряженных с ним относительно поля К элементов, называют нормальным базисом поля F над К. Пример: Пусть aF8 корень неприводимого многочлена x3+x2+1 из F2[x]. Тогда {a,a2,(1+a+a2)} - базис поля F8 над F2. Однозначно определенным к нему дуальным базисом (в данном случае автодуальным) будет этот же базис. Действительно элемент a5F8можно представить в виде a5=c1a+c2a2+c3(1+a+a2), где коэффициенты c1, c2, c3из F2 определяются 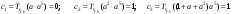 так, что a5=a2+(1+a+a2). Указанный базис является также нормальным базисом поля F8 над F2, т.к. 1+a+a2=a4. Чтобы разобраться в представленном выше примере рассмотрим один из способов представления элементов конечного поля Fq из q=p2 элементов. Идея этого способа базируется на следующих фактах: Поле Fq является простым алгебраическим расширением простого поля Fp. Если f(x) неприводимый многочлен степени n из Fp[x] , то любой корень а этого многочлена принадлежит полю Fpn=Fq и потому Fq=Fp(a). Тогда каждый элемент поля Fq можно однозначно представить в виде значения некоторого многочлена от х над Fp степени не более n -1, при x=a. Например, чтобы представить таким способом элементы поля F9 будем рассматривать это поле как простое алгебраическое расширение степени 2 поля F3, которое получается присоединением корня а неприводимого над F3 многочлена степени 2, пусть это будет f(x)=x2+1F3[x]. Тогда f(a)=a2+1=0 в F9 и девять элементов поле F9 можно задать в виде: p0+p1a, где p0,p1F3. Точнее, F9={0,1,2,a,1+a,2+a,2a,1+2a,2+2a}. Продолжим теперь более детальное рассмотрение элементов теории многочленов над конечными полями ввиду важности ее приложений в криптографии. У каждого ненулевого многочлена f(x) над конечным полем кроме его степени deg(f(x)) имеется еще одна важная целочисленная характеристика – его порядок. Лемма. Если f(x)Fq[x] многочлен степени m1, удовлетворяющий условию f(0)0, то существует натуральное число 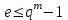 , для которого двучлен xe -1 делится на f(x). , для которого двучлен xe -1 делится на f(x).Этот факт позволяет ввести определение порядка многочлена над конечным полем. Определение. Пусть f(x)Fq[x] ненулевой многочлен. Если f(0)0, то наименьшее натуральное число е, для которого многочлен f(x) делит (xe -1) называется порядком многочлена f(x) и обозначается ord(f(x)). Если же f(0)=0, то многочлен f(x) однозначно представим в виде f(x)=xhg(x) где hN, g(x)Fq[x] и g(0)=0 и тогда ord(f(x)) многочлена f(x) определяется как ord(g(x)). Порядок многочлена иногда называют его периодом или экспонентой многочлена. Порядок неприводимого многочлена можно определить, пользуясь следующей теоремой. Теорема. Пусть f(x)Fq[x] неприводимый многочлен степени m, удовлетворяющий условию f(0)0. Порядок этого многочлена совпадает с порядком любого корня этого многочлена в мультипликативной группе F* поля Fqm. Отсюда вытекает важное следствие: Если f(x)Fq[x] неприводимый многочлен степени m над полем Fq, то его порядок ord(f(x)) делит число qm -1. Значения порядков многочленов играют важную роль при формировании линейных рекуррентных псевдослучайных последовательностей над конечными полями и кольцами, которые в свою очередь являются основой для создания поточных криптосистем. Так как каждый многочлен положительной степени можно записать в виде произведения неприводимых многочленов (каноническая форма представления многочленов), то вычисление порядков многочленов значительно упрощается если знать, как находить порядок неприводимого многочлена и произведения попарно взаимно простых многочленов. Ответ на этот вопрос дают следующие теоремы. Лемма. Пусть с – натуральное число. Многочлен f(x)Fq[x], удовлетворяющий условию f(0)0 делит двучлен xc -1 тогда и только тогда, когда ord(f(x)) делит число с. Следствие. Если е1 и е2 натуральные числа, то НОД многочленов (xe1 -1) и (xe2 -1) в Fq[x] равен (xd -1), где d=НОД(е1, е2). Теорема. Пусть nN и g(x) – неприводимый многочлен над конечным полем характеристики P, такой что g(0)0. Тогда для многочлена вида f(x)=gn(x) имеем ord(f(x))=ord(gn(x))=ptord(g(x)), где t – наименьшее целое число, для которого ptn. Теорема. Пусть g1(x),...,gk(x) – попарно взаимно простые ненулевые многочлены над полем Fq, и пусть f(x)=g1(x)g2(x)...gK(x), тогда ord(f(x))=ord(g1(x))ord(gK(x))=НОК(ord(g1(x),...,ord(gK). Иными словами, порядок произведения попарно взаимно простых ненулевых многочленов равен наименьшему общему кратному порядков его сомножителей (многочленов). Пример: f(x)=x10+x9+x3+x2+1F2[x]. Каноническое разложение f(x) над полем F2 имеет вид f(x)=(x2+x+1)3(x4+x+1). Т.к. ord(x2+x+1)=3 и имея ord(gn(x)=ptord(g(x)), получаем, что ord((x2+x+1)3)=223=12 т.к. у нас F2 т.е. p=2 и t=2 чтобы 22>3). Далее ord(x4+x+1)=15. Тогда ord(f(x))=НОК(12,15)=60. Обобщить эти результаты можно теоремой. Теорема. Пусть Fq конечное поле характеристики p. Если 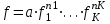 каноническое разложение в кольце Fq[x] многочлена f(x)Fq[x] положительной степени, такого что f(0)0, то каноническое разложение в кольце Fq[x] многочлена f(x)Fq[x] положительной степени, такого что f(0)0, то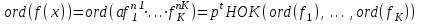 , ,где t – наименьшее целое число, удовлетворяющее неравенству ptmax{n1,...,nK}. Из определения порядка е многочлена f(x) следует, что е это наименьшее натуральное число, удовлетворяющее сравнению: xe1(mod(f(x)), т.к. это сравнение означает, что f(x) делит xe -1. Отсюда следует еще один способ определения порядка многочленов. Согласно приведенному выше следствию 1 порядок е делит число qm -1, где m степень многочлена f(x). Предполагая qm>2 будем исходить из разложения числа qm -1 на простые сомножители: 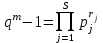 . .Для каждого 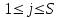 найдем вычеты одночлена найдем вычеты одночлена 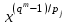 по модулю f(x) (т.е. остатки от их деления на f(x)). Обычно это делается перемножением подходящим образом выбранного набора вычетов по модулю f(x) степеней по модулю f(x) (т.е. остатки от их деления на f(x)). Обычно это делается перемножением подходящим образом выбранного набора вычетов по модулю f(x) степеней 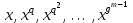 переменной x. При этом, если переменной x. При этом, если 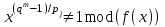 ,то число е делится на ,то число е делится на 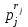 , в противном случае, число е не делится на , в противном случае, число е не делится на 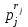 . В последнем случае мы выясняем, будет ли число е делится на . В последнем случае мы выясняем, будет ли число е делится на 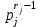 , , 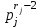 , ..., , ..., 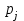 , вычисляя соответственно вычеты по модулю f(x) следующих степеней переменной x: , вычисляя соответственно вычеты по модулю f(x) следующих степеней переменной x: 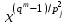 , , 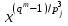 ,..., ,...,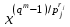 . Такой подсчет проводится для каждого простого делителя pj числа qm -1 и в итоге находится порядок e=ord(f(x)). . Такой подсчет проводится для каждого простого делителя pj числа qm -1 и в итоге находится порядок e=ord(f(x)).В этом методе ключевым моментом является разложение на простые сомножители натурального числа qm -1. Существуют обширные таблицы для полного такого разложения указанных чисел, особенно для q=2 т.е. для полей F2 и F2m. |
